◎正当な理由による書き込みの削除について: 生島英之とみられる方へ:
高校数学の質問スレ Part422 ->画像>37枚
動画、画像抽出 ||
この掲示板へ
類似スレ
掲示板一覧 人気スレ 動画人気順
このスレへの固定リンク: http://5chb.net/r/math/1665137574/
ヒント:5chスレのurlに http://xxxx.5chb.net/xxxx のようにbを入れるだけでここでスレ保存、閲覧できます。
【質問者必読!!】
まず>>1-4をよく読んでね
数学@5ch掲示板用 掲示板での数学記号の書き方例と一般的な記号の使用例
http://mathmathmath.dotera.net/
・まずは教科書、参考書、web検索などで調べるようにしましょう。(特に基本的な公式など)
・問題の写し間違いには気をつけましょう。
・長い分母分子を含む分数はきちんと括弧でくくりましょう。
(× x+1/x+2 ; ○((x+1)/(x+2)) )
・丸文字、顔文字、その他は環境やブラウザによりうまく表示できない場合があります。
どうしても画像を貼る場合はPCから直接見られるところに見やすい画像を貼ってください。
ピクトはPCから見られないことがあるので避けてください。
・質問者は名前を騙られたくない場合、トリップを付けましょう。
(トリップの付け方は 名前(N)に 俺!#oretrip ←適当なトリ)
・質問者は回答者がわかるように問題を書くようにしましょう。
でないと放置されることがあります。
(変に省略するより全文書いた方がいい、また説明なく習慣的でない記号を使わないように)
・質問者は何が分からないのか、どこまで考えたのかを明記しましょう。
それがない場合、放置されることがあります。
(特に、自分でやってみたのに合わないので教えてほしい、みたいなときは必ず書くように)
・回答者も節度ある回答を心がけてください。
・970くらいになったら次スレを立ててください。
※前スレ
高校数学の質問スレ Part420
http://2chb.net/r/math/1658820329/
高校数学の質問スレ Part421
http://2chb.net/r/math/1662638587/ 高校数学範囲で問題の意味が理解できる自作問題で
正解に自信がなくて質問するのもありです。
[2] 主な公式と記載例
(a±b)^2 = a^2 ±2ab +b^2
(a±b)^3 = a^3 ±3a^2b +3ab^2 ±b^3
a^3±b^3 = (a±b)(a^2干ab+b^2)
√a*√b = √(ab), √a/√b = √(a/b), √(a^2b) = a√b [a>0, b>0]
√((a+b)±2√(ab)) = √a±√b [a>b>0]
ax^2+bx+c = a(x-α)(x-β) = 0 [a≠0, α+β=-b/a, αβ=c/a]
(α,β) = (-b±√(b^2-4ac))/2a [2次方程式の解の公式]
a/sin(A) = b/sin(B) = c/sin(C) = 2R [正弦定理]
a = b cos(C) + c cos(B) [第一余弦定理]
a^2 = b^2 + c^2 -2bc cos(A) [第二余弦定理]
sin(a±b) = sin(a)cos(b) ± cos(a)sin(b) [加法公式]
cos(a±b) = cos(a)cos(b) 干 sin(a)sin(b)
log_{a}(xy) = log_{a}(x) + log_{a}(y)
log_{a}(x/y) = log_{a}(x) - log_{a}(y)
log_{a}(x^n) = n(log_{a}(x))
log_{a}(x) = (log_{b}(x))/(log_{b}(a)) [底の変換公式]
f '(x) = lim_[h→0] (f(x+h)-f(x))/h [微分の定義]
(f±g) ' = f ' ± g '、(fg) ' = f 'g + fg ',
(f/g) ' = (f 'g-fg ')/(g^2) [和差積商の微分]
[3] 基本的な記号の使い方は以下を参照してください。
その他については>>1のサイトで。
■ 足し算/引き算/掛け算/割り算(加減乗除)
a+b → a 足す b (足し算) a-b → a 引く b (引き算)
a*b → a 掛ける b (掛け算) a/b → a 割る b (割り算)
■ 累乗 ^
a^b a の b乗
a^(b+1) a の b+1乗
a^b + 1 (a の b乗) 足す 1
■ 括弧の使用
a/(b + c) と a/b + c
a/(b*c) と a/b*c
はそれぞれ、違う意味です。
括弧を多用して、キチンと区別をつけてください。
■ 数列
a[n] or a_(n) → 数列aの第n項目
a[n+1] = a[n] + 3 → 等差数列の一例
Σ[k=1,n] a_(k) → 数列の和
■ 積分
"∫"は「せきぶん」「いんてぐらる」「きごう」「すうがく」などで変換せよ。
(環境によって異なる。) ∮は高校では使わない。
∫[0,1] x^2 dx = (x^3)/3|_[x=0,1]
■ 三角関数
(sin(x))^2 + (cos(x))^2 = 1, cos(2x) = (cos(x))^2 - (sin(x))^2
■ ヴェクトル
AB↑ a↑
ヴェクトル:V = [V[1],V[2],...], |V>, V↑, vector(V)
(混同しない場合はスカラーと同じ記号でいい。通常は縦ヴェクトルとして扱う。)
■行列
(全成分表示):M = [[M[1,1],M[2,1],...],[M[1,2],M[2,2],...],...], I = [[1,0,0,...],[0,1,0,...],...]
(行 (または列) ごとに表示する. 例)M = [[1,-1],[3,2]])
■順列・組合せ
P[n,k] = nPk, C[n.k] = nCk, H[n,k] = nHk,
■共役複素数
z = x + iy (x,yは実数) に対し z~ = x - iy [4] 単純計算は質問の前に http://www.wolframalpha.com/ などで確認
入力例
・因数分解
factor x^2+3x+2
・定積分
integral[2/(3-sin(2x)), {x,0,2pi}]
・極限
limit(t*ln(1+(1/t^2))+2*arctan(t))) as t->infinity
・無限級数
sum (n^2)/(n!), n=1 to infinity
・極方程式
PolarPlot[2/sqrt(3-sin(2t)), {t, 0, 2Pi}]
グラフ描画ソフトなど
・FunctionView for Windows
http://hp.vector.co.jp/authors/VA017172/
・GRAPES for Windows
http://tomodak.com/grapes/
・GRAPES-light for i-Pad
http://www.tokyo-shoseki.co.jp/ict/textbook_app/h/003003
・GeoGebra for Windows / Mac OS X
http://sites.google.com/site/geogebrajp/
入試問題集
http://www.densu.jp/index.htm (入試数学 電子図書館)
http://www.watana.be/ku/ (京大入試問題数学解答集)
http://www.toshin.com/nyushi/ (東進 過去問DB) 以下の【条件】を満たす実数(a,b)の条件を求め、ab平面上に図示せよ。
【条件】
すべての整数mに対して
m^2-am+b>0
が成り立つ。
質問します
xは正の実数xとする。
x^n+(1/x)^nの最小値を与えるxはnによらないことを示せ。
これができれば裏口シリツ医以上の学力があると言える問題
(まあ、中卒以上の学力しか保証されないけどw)

# 0.282*m+0.09*f=0.182*(m+f)
# 0.282*(m/f)+0.09=0.182*(m/f+1)
# m/f=0.92
Pf=1/(1+0.92)
Psmoker=0.282*(1-Pf)+0.09*Pf
0.09*Pf/Psmoker
>>11 男M人、女L人とすると、
0.282M+0.09L=0.182(M+L)
0.1M=0.092L
M=0.92L
L/1.92L=50/96=25/48=0.52833……
∴約52.83%
0.1M+0.8L=0.5(M+L)
0.3L=0.4M
∴M:L=3:4
0<s<1, 0<t<1 とします。P(s,t), Q(s+t,s+t)とします。
s,tがうごくときの、線分PQの通過領域をもとめたいのですが、
おしえてくださあい。
ファクシミリ逆像法をつかうのでしょうか。
よろしくおねがいします。」
いえQ(s+t,s+t)です。xy座標同じです。
よろしくおねがいします。
前
>>13 >>14 たくさん直線PQを重ね描いていくと、
(0,0),(0,2),(2,2),(2,0)を頂点とした正方形内部じゃないかなぁと思う。境界を含まずに。
1≦u≦2に対してP(u-1,1), Q(u,u)とおくときPQの方程式は
(u-1)x - y -u² +2u = 0
uで編微分して
x - 2u+2 = 0
連立して
x = 2u - 2,
y = (u-1)(2u-2) -u² +2u = u²-2u+2 = x²/4+1
∴ 0≦y≦x²/4+1、0≦x≦y²/4+1
これは包絡線を考えてるんしょうか
包絡線は大学生範囲なので高校生範囲でおねがいします
>>14 1000本書いてみた。色分けはトラ模様にw

>>15 Q(s+t,st)で書いてみた(プログラムで書かせてみた)

y=x^2/4+1
y=2*√(x-1)
を追加

高二です。学校で放物線の焦点、準線について扱い、分からない問題があるので教えてください。
Euclid平面上の放物線Cに於いて,其の焦点をF,準線をlとする。
1 放物線Cの二つの接線が直交するとき,その交点Pは準線l上にあることを証明せよ
2 いま二つの接線が直交するとき,その交点Pの軌跡は準線lであることを証明せよ
図形的な解法で解けという指示があり、どうしても分からない問題です。
準線上の動点をP、焦点をF、接点をAᵢ、接点から準線に下ろした垂線の足をHᵢとする
∠A₁PA₂=90°である事を示せば十分
△AᵢPHᵢ≡△AᵢPGより容易
>>26 ありがとうございます。参考させていただきます。
もし、よろしければ次の問題もわからないので教えてください。
Euclid平面上の放物線Cに於いて,其の焦点をF,準線をlとする。
1いま任意の直線mと放物線Cとの共有点は高々2個であることを証明せよ。
2いま放物線C上の任意の点Pから準線lに下ろした垂線の足をHとするとき,∠FPHの二等分線mが放物線Cの接線になることを証明せよ。なお放物線の接線は「放物線と一点のみを共有し,準線の垂線ではない直線」で定義される。
3いま直線pを放物線Cの接線とするとき,直線pの任意の平行線mは放物線Cの接線ではないことを証明せよ。
後で答え書いていい気になる作戦がアッサリ答えられてしかも同じ答えをかぶせるアホ
前
>>17 >>14 やっぱりあってた。
たくさん直線PQを重ね描いていくと、
(0,0),(0,2),(2,2),(2,0)を頂点とした正方形内部。境界を含まずに。ここからつづきがある。
かつ0≦y≦x^2/4
かつ0≦x≦y^2/4
0≦x≦1で定義されたxy平面上の曲線C:y=f(x)=(x^2)√(1-x^)について、Cとx軸とで囲まれる領域の面積を求めよ。
2^n≦n(n+1)(n+2)
となる正整数nをすべて求めよ。
前
>>29 >>30 x=sintとおくとdx=costdt
∫[x=0→1]x^2√(1-x^2)dx=∫[t=0→π/2]sin^2tcos^2tdt
=∫[t=0→π/2]{(1-cos2t)/2}{(1+cos2t)/2}dt
=∫[t=0→π/2][{1-cos^2(2t)}/4]dt
=∫[t=0→π/2](1/4-1/8-cos4t/8)dt
=∫[t=0→π/2](1/8-cos4t/8)dt
=[t=0→π/2][t/8-sin4t/32]
=π/16
質問するスレがあるのはいいことです
質問します
xyz空間のベクトルa,b,cは
|a|+b・c=0
|b|+c・a=0
|c|+a・b=0
を満たす。
このようなベクトルa,b,cの例を1つ挙げ、それ以外にあるかどうかを説明せよ。
(0,0,0)
ある
((2,0,0),(-1,√3,0),(-1,-√3,0))
>>30 作図してみた。

発展問題
0≦x≦1で定義されたxy平面上の曲線C:y=f(x)=(x^2)√(1-x^2)について、Cの長さを求めよ。
小数4桁までよい。(厳密解はしらんのでw)
>>27 集合Rがあり、2つの演算、加法+と乗法×が定義されているとする。すなわち
任意のa, b∈Rに対して
a+b∈R、a×b∈Rとなるものとする。
ここでRは実数の集合ということではない。
>>30 ∀a b c (a+b)+c=a+(b+c)
∀a ∃0 a+0=0+a=a
∀a ∃x a+x=0
∀a b a+b=b+a
∀a b c (a×b)×c=a×(b×c)
∀a ∃1 a×1=1×a=a
∀a b c (a+b)×c=a×c+b×c
a×(b+c)=a×b+a×c
+に関して結合法則、 交換法則、単位元、逆元、
×に関して結合法則、単位元
+と×に関して左右の分配法則
×に関して逆元、交換法則は無い。
立方体があります(中身は考えずsurfaceのみ考えます)。
この立方体の12本の辺から無作為に異なる7本を選ぶとき、
選んだ7本の辺を切り開いた時に展開図ができる確率は求めるのは難しいでしょうか。
>>31 正確に言えば「(R, +, -)が環である」というところを慣用で「Rは環である」と言う。実際には集合として同じRであっても演算の定義によって環としては異なる場合もある。
>>39 ググってみると立方体の展開図は回転、線対称で移り合うものを同一視して11種類であるそうな
https://happylilac.net/zukei-rippotaitenkaizu.html 線対称軸を持つもの2種、持たないもの9種
線対称軸を持つ展開図になる7辺の選び方は24×2=48
線対称軸を持たない展開図になる7辺の選び方は48×9=432
合わせて480通り
12個の中から7個選ぶのは₁₂C₇=792
確率は
480/792 = 20/33
>>33 R=Zとすると環になる。整数環。
有理数、実数、ふくそすう全体の集合Q、R、Cは環である。
n次実正方行列全体の集合M(n,R)は環である。零行列0、単位行列1。
有理行列全体の集合M(n,Q)や複素行列全体の集合M(n,C)も考えられ、環になる。
一辺の長さが1の立方体をその1つの対角線Lを軸に1回転させてできる立体をKとする。
KをLを含む平面で切った切断面の面積を求めよ。
>>36 法mの合同類全体Z/mZは環である。
(1) R²において(a,b)×(c,d)=(ac+2bd, ad+bc)で定義すると環になる。
(2) (a, b)x(c, d)=(ac, ad+bc)で定めても環になる。
(1)(2)により集合としては同じでも演算が異なるので環としては異なる。環Rのち翌積R×Rも環であるがこれも集合としては一致しても環としては異なる例になる。
>>43 実数値連続関数全体の集合C⁰(I, R)は環てである。簡単に思えるが「連続関数の和と積はそれぞれ連続関数である」という定理に基づいていることに注意。
複素数平面C内の開集合Dの上の複素数値正則関数全体の集合O(D)は環てある。
加法に関して可換群をなす。
ちょっと質問させてください
根本的に勘違いしてるのかもしれませんが
100円BIGの確率なんですが
どういう計算で480万分の一になるんでしょうか?
https://www.rakuten-bank.co.jp/toto/big/100big.html 指定された14試合を対象に
1か2か0で3分の一で、その14乗じゃないんでしょうか?
1等 約1/480万
2等 約1/17万
3等 約1/1万3000
4等 約1/1,643
5等 約1/299
とあるので、1等上がるごとに3分の一を掛けてるわけじゃないのは分かるんですが
>>35 ∀a, a×x=x×a=a、a×y=y×a=a
とする。
a=yとするとy×x=x×y=y、
a=xとするとx×y=y×x=x
よってx=yとなり一意性が示された。
>>7 ×を+にするだけで全く同じである。
∀a, a+x=x+a=a、a+y=y+a=a
とする。
a=yとするとy+x=x+y=y
a=xとするとx+y=y+x=x
よってx=yとなり一意性が示された。
>>8 a+x=0、a+y=0とする。
両辺にyを加えると
a+x+y=0+y=y
両辺にxを加えると
a+y+x=0+x=x
和に関する交換法則により
a+x+y=a+y+xであるからx=y
よって逆元の一意性が示された。
>>46 1/3の14乗を計算すると約480万分の1なので
何もおかしくないと思うが
2等以下は反復試行の確率
>>11 ∀a, b∈R、∃y∈R、a+y=b
aに対して∃x、a+x=0となる。
両辺にxを加えると
a+y+x=b+x
y+a+x=y+0=y=b+x
逆にbを加えると
a+x+b=b
ここでy=x+bとおくと
a+y=bとなる。
易しい質問をします。
kを複素数の定数とする。
a,b,cの連立方程式
1+ka=b
1+kb=c
1+kc=a
を解け。
>>11 環Rの零元0(R)、単位元1(R)、加法に関するaの逆元-a、
0+0=0
両辺に右からaをかけて
0a+0a=0a
両辺から0aを引いて
0a=0
両辺に左からaをかけると
a0=0が導かれる。
>>50 反復試行の確率ありがとうございました
>>5 のページで計算したら480万分の一でした
初めてでしたが、分かりやすくて便利でした
>>52 定義によりa+(-a)=0
同様に(-a)+(-(-a))=0
よって(-(-a))+(-a)=a+(-a)
∴-(-a)=a
分配法則より
ab+a(-b)=a(b+(-b)=a0=0
よってa(-b)=-(ab)
同様に0=(a+(-a))b=ab+(-a)b
よって(-a)b=-(ab)
これらを使って
(-a)(-b)=-((-a)b)=-(-(ab))=ab
a+(b-a)=a+b-a=a-a+b=0+b=b
両辺に(-a)を加えると
(-a)+a+(b-a)=b+(-a)
∴b-a=b+(-a)
>>52 零環、ゼロリング
R={0}、0だけからなる環
Z/mZにおいてm=1とすると零環になる。
Rを環とする。
Rは零環⇔1(R)=0(R)
>>43 Rが零環ならば1(R)=0となる。
環Rにおいて1=0とする。
∀a a×1=1×a=a、a×0=0×a=0
するとa=a×1=a×0=0
a=1×a=0×a=0
よって任意の元が0であるからこの時Rは零環である。
放物線上の点P における接線PT をひくと,
∠FPT = ∠HPTが成り立つ.(点 F は焦点,g は準線.また線分PH は,点P から準線に引いた垂線)
という有名な定理(?)性質について習いました。この逆、
つまり∠FPHの二等分線mが放物線Cの接線になる
ことはどう証明すればよいでしょうか??
>>7 可換環ならば二項定理が成り立つが非可換環では二項定理は成り立たない。AB+BA=2ABとは出来ない。
Hamiltonの四元数環
i²=j²=k²=-1(虚数単位)
i×j=k、j×k=i、k×i=j
i×j=-j×i、j×k=-k×j、k×i=-i×k (外積)
>>58 (a,b,c,d)×(e,f,g,h)=
(ae-bf-cg-dh,af+be+ch-dg,
ag+ce-bh+df,ah+de+bg-cf)
上の放物線の問題、先ほど自分で解決しました。すいません。
いま直線pを放物線Cの接線とするとき,直線pの任意の平行線mは放物線Cの接線ではないことを示せ
この問題、方針だけでもいいので教えてください。幾何的に解いていただけるとありがたいです
すいません、私馬鹿なのでもう少しだけわかりやすくお願いします
>>61 +と×について閉じている
加法に関する逆元を持つ
1(R)を含む
この時、部分集合R'をRの部分環という。
Z⊂Q⊂R⊂Cの包含関係に応じて部分環が作れる。
2次実上三角行列全体の集合は2次実行列全体の集合の部分環である。非可換である。
回転拡大の行列は可換な部分環である。
本当にすいません、高校生なもので皆様の解説が理解不能です。
幾何で証明していただけるとありがたいです
そりゃ無理だ
放物線の接線の持つ性質の無限にある幾何的性質の「どれは証明されていると仮定していいのか」がわからない限り証明なんぞできん
説明が足りずにすいません...
準線、焦点絡みの諸性質や、高校までに扱う性質なら大丈夫です。
よろしくお願いします。
じゃあ
p//q, p,qは共に接線でA,Bがそれぞれの接点とする
A,Bから準線に下ろした足をH,KとしてAH//BK、p//qよりAF//BF
∴AF = BF
A≠Bならp//qにはなり得ないからA=B
夜遅くにわがままに付き合っていただきありがとうございました。
こういう現実的じゃないというか、別に証明しなくてもわかるくらい当たり前じゃん...と思うような問題の証明が
すごく苦手で...当たり前って思ってる時点でダメかもしれませんね()
とにかく、教えていただきありがとうございました!
イヤ、もっと簡単やな
p//qが共に接線でU,Vをp,qを境界とする閉半平面のうち放物線を含む側とする
U⊂Vとしてよい
U≠VならUの任意の点からqまでの距離は平行線pq間の距離d以上である
特にqと放物線上の任意の点とqの距離は常にd以上で矛盾
>46に触発されてこんな問題を考えた。
https://www.rakuten-bank.co.jp/toto/big/100big.html
>>
購入する口数を決めるだけ。
(指定された14試合を対象にホームチームの90 分間での勝ち=「1」、負け=「2」、その他(引き分け・延長)=「0」をコンピュータがランダムに選択します。お客さまが予想する必要はありません)
14コの数字のうち
1等 すべての数字が一致
2等 1コはずれ
3等 2コはずれ
4等 3コはずれ
5等 4コはずれ
<<
に加えて次の当選条件も加える
6等 5コはずれ
7等 6コはずれ
8等 7コはずれ
...
12等 11コはずれ
13等 12コはずれ
14等 13コはずれ
15等 14コはずれ
【問題】
(1) 何等が一番あたりやすいか?
(2) それがあたる確率を求めよ 全部当たるのも難しいが、全部外れるのも難しそう。
(1)は答が2個あると思う。
(2)を乱数発生させてシミュレーションして確率分布を出してみた。

理論値
> cbind(何等賞,何人に一人)
何等賞 何人に一人
[1,] 1 4782969.000000
[2,] 2 170820.321429
[3,] 3 13140.024725
[4,] 4 1642.503091
[5,] 5 298.636926
[6,] 6 74.659231
[7,] 7 24.886410
[8,] 8 10.887805
[9,] 9 6.221603
[10,] 10 4.666202
[11,] 11 4.666202
[12,] 12 6.416028
[13,] 13 12.832055
[14,] 14 41.704180
[15,] 15 291.929260
5等賞は全部ハズレの場合にしても元の5等賞とあまり変わらんな。
時間があるので簡単な質問をします。
2nCn≧1000となる最小の自然数nを求めよ。
次の極限が0でない定数に収束するような実数kの値を求めよ。
lim[x→0] {(1+sin(nx))-cos(x)}/(x^k)
>>75 微分可能な関数は連続関数である。
微分可能な関数は+と×に関して閉じている。
よってC∞はC⁰の部分環である。
>>76 Z[i]={a+bi|a,b∈Z}はCの部分環である。ガウス整数環
Z[√2]={a+b√2|a,b∈Z}
Z[³√2]={a+b³√2+c³√4|a,b,c∈Z}
環Rの中心Cent(R)
これはRの部分環となる
∀r∈R、ar=raとなるaのこと。
> f=\(n) choose(2*n,n)
> n=1:10
> n[f(n)>=1000][1]
[1] 7
>>75 部分環R"が{0}とすると
1(b)=0
定義より1(b)=1(a)であるから
1(a)=0
よってRも零環である。
>>78 連立方程式
x+y=2
2x+y=3
を解け
>>76 1(R)∈R"
を部分環の定義に含むか否かは本によって異なる。
Map(X,R)={f|f:X→R}
C⁰(I,R)齒Map(I,R)の部分環である。
R上の多項式の作る環R[T]
>>75 a,b∈R、Rは零環以外の環とする
ab=ba=1となるときaを可逆元または単数という。可逆元全体の集合をR×と表す
>>75 仮定より1≠0であるから0∉R×
1×1=1より1∉R×、1⁻¹=1
aㇷR×の時、a⁻¹∈R×であり
a(a⁻¹)=1より(a⁻¹)⁻¹=a
(b⁻¹a⁻¹)(ab)=b⁻¹1b=b⁻¹b=1より
(ab)⁻¹=b⁻¹a⁻¹である。
>>85 命題「x^2-x=y^2-yならばx=y」の真偽を述べよ。
>>76 Z[i]×={±1, ±i} 4個の元から成る集合
Z×={±1} 2個の元からなる集合
a²-2b²=±1の時、Z[√2]×となる。
=±(a+b√2)n
>>81 0による割り算以外は自由に出来る集合を体という。可換であることも定義に入れておく。
有理数体Q、実数体R、複素数体Cはそれぞれ0による割り算以外は+-×÷が自由に出来る。0による割り算は出来ない。
>>84 Q(i)={a+bi|Ab∈Q}は体である。
これが可換環であり零環でないことを確かめて逆元の存在を示す。
逆元が存在すればその数で割れる。もちろん0以外の元による割り算だけを考えればよい。
>>88 連立方程式解けないの?
wikipediaのコピペ貼る前に中学数学解けるようになろうな
>>88 練習問題
連立方程式
x=1
x+y=0
を解け
>>86 有限体Fp、有理関数体。
非可換なものは体とは呼ばずに斜体または可除代数と呼ぶ。
体はあくまでも環の特別なものと考える。ある種の良い性質を持った環を体として区別しているだけ。
>>81 左零因子aはab=0、b≠0
右零因子aはba=0、b≠0
冪零元aはa^k=0となるkが存在する。
前
>>32 >>43 {(√3/2)√2}^2=3/2
>>84 0は左零因子である。0は幹零因子である。0は冪零元である。
可逆元aがあるbに対してab=0
となったとする。両辺に左からaの逆元を掛けるとb=0となる。ba=0の場合も同様である。
aを壁零元とする。a^k=0となるkが存在する。そのようなkのうちで最小のものを取る。k=1の時はa=0であり証明済みである。k>1とする。
a^(k-1)=bとおくとb≠0
ab=ba=0となるので冪零元aは左零因子であり、右零因子である。
>>86 可逆元aが零因子であると仮定する。a^k=0を満たすkが存在するのでその最小のものを取る。
aの逆元を両辺に掛けることによりa=0となるがこれは仮定に反する。
>>81 可逆元⇒¬左零因子∧¬右零因子
冪零元⇒左零因子∧右零因子
⇔¬(左零因子∨右零因子)⇒¬冪零元
これらから可逆元⇒¬冪零元となる。
>>84 行列環
可逆元⇔可逆行列⇔正則行列⇔detA≠0⇔rankA=n⇔∀i、αi≠0
この環においては左零因子⇔右零因子である。
Aが冪零元⇔∀i、αi=0
>>86 可換環である
零環ではない
0以外の零因子を持たない
このような環を整域と言う。
四元数環は0以外に零因子を持たないが可換環でないので整域とはならない。
>>81 bは素数⇔Z/pZは体⇔Z/pZは整域
m=1の時、Z/mZは零環になるので成り立つ。
mが合成数の時、m=m₁m₂(m₁,m₂>1)
m₁≡0ではなくm₂≡0ではないがm₁m₂≡0となるから0以外の零因子が存在し整域とはならない。
p元体Fp=Z/pZ (pは素数)
>>84 分数体Frac(R)
a=a/1(R)によりRはRの分数体の部分集合になる。分数体は商体Quot(R)とも言う。
Frac(Z[i])=Q[i]
環については可換環と非可換環
体については体と斜体(可除代数)
すいませんここで質問してもいいですか?荒らしだらけですけど
過去の京大の問題でy=sin(x^3)が周期関数でないことを示せというものがありました
当たり前にしか見えないのですが示せと言われると記述に困りました
背理法でしょうか?
sin(x^3)が周期関数なら導関数も周期関数で有界
でも、実際に導関数を計算するとそんなこたあない、矛盾
みたいな筋でいいんじゃないの
f(x)=sin(x^r)が周期関数となる実数rをすべて求めよ。
>>102 京大なら
aを最小周期とするとx\to\inftyのとき区間[x,x+a]内の
零点の個数がいくらでも大きくなるから
でも通りそう
>>104 deg(0)=-∞と定義する
deg(a₀)=0 (a₀≠0の時) である
代入はΦ(f(T))=f(α)
∀a∈Rに対して
f(T)=a (定数多項式)とすると
Φ(a)=aとなる。
-1≦sin(x)+cos(x^2)≦1
0≦x+x^2≦2π
を満たすxのうち最大のものを求めよ。
>>7 有理関数体k(T)
Frac(Z[T])=Q(T)
K[T]は環、K(T)は体とするので
Z[T]はあるが、Z(T)は無い。
K[T]は体K上の多項式環=多項式、
K(T)は有理関数体=分数式。
Z[i]とQ(i)も同じ。
k^2-40=3^m
を満たす正整数(k,m)をすべて求めよ。(千葉大・医)
>>108 多変数単項式の総次数
多変数多項式の総次数
n次の斉次多項式は零多項式も含む。
R[T₁,T₂]=R[T₁][T₂]
LHS ≡ 0,1 ( mod 4 )
So is RHS
∴m : even
n := m/2
(k + 3ⁿ)(k-3ⁿ) = 40
(k + 3ⁿ, k-3ⁿ) = (20,2),(10,4) (∵ both must be even and positive)
(k,m) = (11,4),(7,2)
>>110 R[T₁][T₂]=R₁[T₂]と考えて良い
すなわちf(T₁,T₂)をT₂の多項式g(T₂)と見ることが出来、その各項の係数はR[T₁]の元である。
>>110 Rは整域であり、
Rが整域⇒R[T₁]は整域
であるからR₁[T₂]は整域である。従ってR[T₁,T₂]は整域である。
帰納的に、n変数多項式について成り立つ。n≧1。
>>104 Rの部分集合I
I≠∅
a,b∈I⇒a+b∈I
a∈I、r∈R⇒ra∈I
環Rの部分集合であり、空集合でなく、和に関して閉じていて、r∈R倍は全て含む集合。Rの元rを左から掛けるので左イデアルと言う。
右イデアル、両側イデアルもある。
>>108 a∈I、0∈Rより0a=0∈I
-1∈Rより-1a=-a∈I
b-a=b+(-a)∈I
1∈I⇒r∈R、1r=r∈I
IはRの部分環であるが条件は単なる部分環よりも厳しい。和は全く同じで積は違う、単位元も違う。
>>104 自明なイデアルとして{0}=零イデアルとR自身がある。これらはどんなイデアルにも含まれる。
(1)a,bを実数の定数とする。xの方程式x^3-ax=x^2-bxを解け。
(2)xy平面上の2つのグラフ
y=x^3-ax
y=x^2-bx
で囲まれる部分が存在するような実数a,bの範囲を求めよ。
(3)a,bが(2)の条件を満たすとき、(2)の2つのグラフで囲まれる領域の面積をa,bで表せ。
>>108 Iは0を必ず含むので多項式環R[T]は零多項式を含まなければならない。よってf(a)=c=0が必要である。もしc≠0ならばIはRのイデアルとはならない。f:a→cとなる多項式全体の集合。f(a)∈Iよりf(a)=0、g(a)∈Rよりg(a)=0とは限らない。
>>119 Nil(R)、可換環Rにおいて冪零元全体の集合。Rの=零根基と言う。
0∈Nil(R)である。0¹=0
a,b∈Nil(R)とすると
(a+b)^N=0 (N≧m、N≧n)より
a+b∈Nil(R)
Rは可換環であるから、r∈Rとして(ra)^n=r^n×a^n=0より
ra∈Nil(R)
よってNil(R)はRのイデアルである。
イメージが沸かないので
y=sin(x^3)とその導関数のグラフを書いてみた。


前
>>94 >>119 (1)x^3-ax=x^2-bx
x=0,{1±√(1+4a-4b)}/2
学校の宿題で困惑しているところがあります
早稲田商の問題で(2+√3)^2000の小数部分を求めさせる問題がありました。ノーヒントの穴埋めです。
これに対して解答ではいきなり(2-√3)^2000を持ち出してきて(2+√3)^2000+(2-√3)^2000は整数だから~としてあるのですが、このタイプの問題ではこれが定石だから覚えるしかないのでしょうか
早稲田商の数学の難易度は異常と聞いているので普通は(2-√3)^nを持ってくる誘導がつくものでしょうか
>>122 導関数のグラフはこれ

>>8 RaはRの左イデアル。単項左イデアルと言う。aRは単項右イデアルと言う。(a)とも書く
自明なイデアル{0}=(0)、R=(1R)は単項イデアル。
>>124 いきなり2000乗と言われてもふつうは計算できないが
問題として出されればトリックを探そうという気になる。
そこで「やさしい計算に帰着させることができれば」という方向で
考えることができるかが問われていると思われる。
0.1の2000乗の小数点以下を100桁まで求めるのは容易。
>>7 1∈R、a=a∈(a)。
a∈I、r∈R⇒ra∈Iより(a)⊂I
(a)=R⇒∃r∈R、ra=1⇔a∈R×
逆にa∈R×ならばa(a⁻¹)=1より
(a)=R。(6)⊂(3)、6∈(3)、6=3×2
期待値は小中学校の範囲外みたいなので、少し変えて投稿。
子どもが3人いて次の条件が判明している。(条件付き確率で計算しろというヒント)
(少なくとも)一人は土曜日か日曜日に生まれた女児である。
【問題】
(1)3人とも女児である確率を求めよ。
(2)この3人の中に何人女児がいるか、その期待値を求めよ。
(3)条件を(少なくとも)一人は女で日曜日に生まれた女児であるとしたときの、3人とも女である確率と女児の数の期待値を求めよ。
少なくとも一人は土日生まれでn人が女子である確率をp(n)とすると
p(1)=3C1*(1/2)^3*2/7=3/8*2/7=294/(8*7^3)
p(2)=3C2*(1/2)^3*(1-(1-2/7)^2)=3/8*24/7^2=504/(8*7^3)
p(3)=3C3*(1/2)^3*(1-(1-2/7)^3)=1/8*218/7^3=218/(8*7^3)
p(3)/(p(1)+p(2)+p(3))=218/(294+504+218)=218/1016=109/508
(1*p(1)+2*p(2)+3*p(3))/(p(1)+p(2)+p(3))=(294+2*504+3*218)/1016
=1956/1016=489/254
上の2/7を1/7に置き換えて再計算するだけ
>>130=尿瓶ジジイは板名も読めないのに自分のこと医者だと思ってるマルチポストシゾ患者です
http://2chb.net/r/hosp/1666045702/ >131
早々のレスありがとうございます。
俺の想定解と一致
土日に生まれた女児がいる時
女児が1,2,3人の確率
147/508 63/127 109/508=0.2893701 0.4960630 0.2145669
女児の人数の期待値
489/254=1.925197
日曜に生まれた女医がいる時
女児が1,2,3人の確率
147/547 273/547 127/547 = 0.2687386 0.4990859 0.2321755
女児の人数の期待値
1074/547=1.963437
土日に生まれたか、日曜に生まれたかの条件の違いで期待値に差がでるのが、俺の直感には反して気持ちが悪い。
こういう設定にすると、3女児の確率も期待値も曜日条件には影響を受けないのは、直感に合致するんだけど。
子どもが3人いる。
(少なくとも)一人は土曜日か日曜日に生まれた。
(少なくとも)一人は女児である。
数学版に投稿すると速攻で正解が返ってくるなぁ。
底辺シリツ医スレに投稿しても、尿瓶おまる洗浄係が無意味なレスを返してくるだけだったが。
円ドルのスレでこういう質問をしたら検算してくれた人がいて、合っていると言われた。
148.800円のときレバレッジ1000で100万ドル買ったとして145.000まで下落したとする。
証拠金維持率が20%を切ると強制ロスカットとすると、ロスカットを避けるにはいくらの証拠金が必要か?
ボーナスポイントやスワップは0として計算せよ。
やっぱり、餅は餅屋だな。
尿瓶おまる洗浄は職種の言えない医療従事者=尿瓶おまる洗浄係に委ねるのが( ・∀・)イイ!!
3829760円になったけど、合っている?
日曜に生まれた女医がいる時
↓
日曜に生まれた女児がいる時
>>134 アンタが板名も読めないアホなだけw
で、医師板の先生には相手にされてないから自分でスレ建てたけどそこでも結局脳内医者丸出しでバカにされてるじゃんw
女児が日曜日に生まれたか、土日のどちらかに生まれたかで
女児の数の期待値が変わる。
日曜日か土日に生まれたか子供がいるとういう条件では期待値は不変。
確率はあなたの心の中にあります!という理解でいいのか?
二人の子供のうち少なくとも一人は例えば一億人に一人の病気を持つ女児だとすると
(女女)でそうなる確率は(1-(1-1/億)^2)≒2/億
(男女)でそうなる確率は1/億
(女男)でそうなる確率は1/億
となるのでこういう事前情報があると女一人だとレアケースが起きたことになり
女二人である場合の方が二倍も起きやすいといえる
一方で事前情報がないとこれらの確率は等しいとして扱うので全然違う
(1)k^2-40=3^mを満たす正整数(k,m)をすべて求めよ。
(2)l^2-41=3^nを満たす正整数(l,n)は存在するか。
>>139 解説ありがとうございます。日曜日に生まれた=罹患率1/7の病気に罹患した女児が少なくとも一人いる、と設定できますね。
子供二人で少なくとも一人は日曜日に生まれた女子であるとき
子供がどちらも女児である確率を求めよ。
日曜日に生まれた=罹患率(p)=1/7の病気に罹患している、と考えて
pを変化させて、子供がどちらも女児である確率をグラフ化。
土日のどちらかに生まれたらp=2/7
1/7,2/7,..,7/7を+で表示
0.4814815 0.4615385 0.4400000 0.4166667 0.3913043 0.3636364 0.3333333
13/27 6/13 11/25 5/12 9/23 4/11 1/3

んで、それを発展させて臨床応用。
人口性比(女性100人に対する男性の数)は95.8
即ち、男女比95.8:100
https://www.stat.go.jp/data/kokusei/2000/kihon1/00/02.html コロナ患者の男女比54:46
https://www.komei.or.jp/km/nakane-takuya-koto/files/2020/03/ed2af0e21c561c6ab0453fd85f9b0721.pdf ある病院の発熱外来では40%が新型コロナが陽性である。
受診者や陽性の男女比は不明なので上記の男女比を使うことにする。
患者が2人発熱外来を受診して一人は新型コロナ陽性の女性であった。
もう一人の患者が新型コロナ陽性の男性である確率を求めよ。
>>143 こういう話に繋がらないということがいつまでもいつまでもいつまでもわからない能無し
こういう問題を医師国試に出題すれば裏口シリツ医が排除できるのに。
スレタイもろくに読めない尿瓶ジジイはお引き取りください
もっとも医師板でも脳内医者ってバカにされるだけだもんな
このスレはもう終わりですね
荒らししかいない
先日y=sin(x^3)の周期性について質問しましたが解答作ってくれた人いなかったですし
質問させてください
n^2-41=3^k
を満たす正整数(n,k)は存在するか
右辺≡0 n≡0のとき 左辺≡0-(-1)=1 n≡±1のとき 左辺≡1-(-1)=2 (mod3)
(1)nを正整数の定数とする。
n^2-n < (n+1)^2-(n+1)
を示せ。
(2)n^2-n < x^2-x < (n+1)^2-(n+1)
を満たす実数xの範囲をnで表せ。
>>155 x^2-x>n^2-n
(x-n)(x+n)-(x-n)>0
(x-n)(x+n-1)>0
よって
x>nかつx>1-n
nは正整数よりx>n...①
x^2-x<(n+1)^2-(n+1)
x^2<n^2+n
-√(n^2+n)<x<√(n^2+n)...②
①、②、n<√(n^2+n)、-√(n^2+n)<nより
n<x<√(n^2+n)...(答)
ある数学の論文で 次のようなことをみたが、意味が分からないので説明よろしく
いくつかの実数 xに対して f(x) >0 であれば任意の実数 t に対して
t < xf(x)-f(f(x)) / f(x) は自明である
こんなもんは画像でも貼らないと信憑性ないし、明らかなすれ違いやろ
ネタか?
>>159 能無しが読み違えてるだけにしか見えんって意味だよ
能無しさん
>>161 その式見て「わからない人間がいる」と一瞬でも思える時点でお前の能無しレベルは見て取れるんだよお馬鹿さん
身の程を知りたまえ
任意の実数 t に 対して
t < xf(x)-f(f(x)) / f(x)
がいえるようなときは、 要するに、 t < ∞
いくつかの実数 x に対し f(x) > 0 なら分母をいくらでも小さくすると
f(x)= 1/1000 のときに
t < 1000x - f(1/1000)
これは任意の xに対し、いくらでも大きくなるから、 t < ∞
自然数 1からN までについて、それらの総和を考える。
S = Σ[k=1,n] (k)
次に、自然数 1からN までについてそれら立方数の総和を考える。
T = Σ[k=1,n] (k^3)
ここで、n = 5 とするとS、Tは それぞれ…
・S = (1+2+3+4+5) ^2 = 225
・T = 1+8+27+64+125 = 225
となる。
ここで 「S^2 = T」 となっているでしょう?
問い.1
「Nが自然数であれば S*S = T が成立する」
(言い換えると、 「連続する自然数の1次」の総和を自乗したものは、
「連続する自然数の3次」の総和と等しくなる)
これは真であるか?
そうであるならば、それを証明せよ。
偽であるならば反例を挙げよ。 (ニュー速小学校 前期 2022)
高校生スレへの出題なら
両方(n(n+1)/2)^2で等しい
で終わりやん
Σ[k=1,n] ( k(k+1) - k(k-1) ) = 2Σ[k=1,n]k
∴ Σ[k=1,n]k = n(n+1)/2
Σ[k=1,n] ( k²(k+1)² - k²(k-1)² ) = 4Σ[k=1,n]k³
∴ Σ[k=1,n]k³ = n²(n+1)²/4
前
>>123 >>30 x=sintとおくとdx=costdt
∫[x=0→1]x^2√(1-x^2)dx=∫[t=0→π/2]sin^2tcos^2tdt
=∫[t=0→π/2]{(1-cos2t)/2}{(1+cos2t)/2}dt
=∫[t=0→π/2][{1-cos^2(2t)}/4]dt
=∫[t=0→π/2](1/4-1/8-cos4t/8)dt
=∫[t=0→π/2](1/8-cos4t/8)dt
=[t=0→π/2][t/8-sin4t/32]
=π/16
これ、あってんの?
1/2*∫[0,1]t^(1/2)(1-t)^(1/2)dt=1/2*B(3/2,3/2)=1/2*(√π/2)^2/2=π/16
∫[0,π/2]sin^2tcos^2tdt=∫[0,π/2](-sin4t+sin2t)dt=π/2{-3!!/4!!+1!!/2!!}=π/16
rを実数の定数とする。
rの値により場合を分けて、極限
lim[n→∞] √{n^2+n^r} - n
を求めよ。
r\leq2-->=0
r>2-->=\infty
前
>>167 >>168√πや、
>>169階乗の階乗を経由しても同じ値になるみたいだから、あってるってことね。
(1)lim[n→∞] √{n^2+n} - n を求めよ。
(2)lim[n→∞] √{n^2+log(e^n+1)} - n を求めよ。
>>177 じゃ、リクエストに応えて
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
みなさん、ご唱和願います
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
もう1コーラス
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>171 求めた答が正しいかどうか、極限に対する感性が試される良問
r=2で答えが0でない有限確定値に収束しないんじゃクソ問
>>151 周期 a があれば、任意のxに対して sin((x+a)^3)=sin(x^3)・・・みたいな解答例が欲しかったのでは
任意のxに対して成り立つとすると aが正、kが自然数としてx=kπ/aでも成り立つから
(x+a)^3-x^3=3ax(a+x)>3ax=3kπ 周期中に零点がいくらでもあることになり矛盾
どこかの1周期ぶん区間内の零点が有限個
なことを言っておかないと、何と矛盾してるのかわかんない
ヨコ
それはpを基本周期として
[0,p)での零点の個数
= sin(x³) = 0, x∈[0,p)となるxの個数
= sin(y) = 0, y∈[0,p³) となるyの個数
なので有限
a^3<nπなる自然数nがあって[0,nπ)にある零点の個数nを超えないのは明らか
x^2+y^2≦3のとき、x-y-xyの最大値を求めよ。(22早稲田商)
x-y = u、-xy=vとおいて
u² - 2v ≦ 3, u²-4v ≧ 0におけるu+vの範囲
以下ry
>>175 傑作です。
(1)から(2)への流れが美しいです。
解いてください。よろしくお願いします。
西暦≡0(mod4)の年をうるう年としてそれ以外は考えない
365=364+1=7*52+1 うるう年でない年の一年後の今日は曜日が一つ上がる
うるう年の一年後の今日は曜日が2つ上がる
今年の二年後はうるう年だから 4m-2≦n-1<4(m+1)-2 であれば
n-1年後までにm回うるう年があるので n年後の今日は曜日がn+mだけ上がる
つまり {(n+1)を4で割った整数部分+n}を7で割った余り だけ曜日が上がる
前
>>176 >>175(1)0
∵√ の中がnよりもn^2の影響を強く受ける、
nを∞に飛ばしたとき。
√{n^2+n} - n=n/{√(n^2+n)+n}
√{n^2+log(e^n+1)} - n=log(e^n+1)/{√{n^2+log(e^n+1)} + n}
={log(e^n)+log(1+e^-n)}/{√{n^2+log(e^n)+log(1+e^-n)} + n}
J = ⌊365.25y⌋+⌊y/400⌋-⌊y/100⌋-⌊30.59×(11-2)⌋+23-678912
J ≡ 0 ( mod 7 ) ⇔(水)
J ≡ 1 ( mod 7 ) ⇔(木)
J ≡ 2 ( mod 7 ) ⇔(金)
J ≡ 3 ( mod 7 ) ⇔(土)
J ≡ 4 ( mod 7 ) ⇔(日)
J ≡ 5 ( mod 7 ) ⇔(月)
J ≡ 6 ( mod 7 ) ⇔(火)
https://ja.m.wikipedia.org/wiki/%E3%83%A6%E3%83%AA%E3%82%A6%E3%82%B9%E9%80%9A%E6%97%A5#cite_note-naoj2-5 >>192 解けました!!
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>199 傑作です。
第一ヴァースから第2ヴァースへの流れが美しいです
歌ってください。よろしくお願いします。
nが自然数とする。
√(n+1) - √n が整数係数の二次方程式の解になるのは、
n+1かnが平方数のときに限りますか?
誰一人として正解にたどり着かない…
難しいんですかね
(1)lim[n→∞] √{n^2+n} - n を求めよ。
(2)lim[n→∞] √{n^2+log(e^n+1)} - n を求めよ。
1/(√1+1/n)+1)→1/2
(1+1/n*log(1+e^-n))/(√(1+1/n+1/n^2*log(1+e^-n))+1)→1/2
ロピタルの定理を使わない方法を教えてください。
よろしくお願いします。
(問題)
lim[x→π/4] {√(sinx)-√(cosx)}/{x-(π/4)}
を求めよ。
>>206 > ロピタルの定理を使わない方法を教えてください。
> よろしくお願いします。
>
> (問題)
> lim[x→π/4] {√(sinx)-√(cosx)}/{x-(π/4)}
> を求めよ。
= lim{√(sinx)-√(sin(π/4))-√(cosx)+√(cos(π/4))}/{x-(π/4)}
= ( √(sinx) - √(cosx) )' (π/4)
√(sinx)-√(cosx)=(sinx-cosx)/(√(sinx)+√(cosx))=sin(x-π/4)*√2/(√(sinx)+√(cosx))
{√(sinx)-√(cosx)}/{x-(π/4)}→√2/(1/√2+1/√2)=1
間違えた √2/(√(sinx)+√(cosx))→√2/(√(1/√2)+√(1/√2))=√2/(2/√√2))=1/√√2
x→0における sin(x)/x の極限値を求めるのにロピタルの定理使うんじゃねーよ、
って話じゃないのか?まあ、使ったら循環論法になるんだが。
そもそも、
>>206は頭が悪いので有名な自作爺さんじゃねーの?
相手にすんなよ。
ちょっと友人から遊びで出されたサイコロの問題で悩んでるから助けて欲しい
※※
六面サイコロと、A〜Hの8つのアルファベットが書かれたトーナメント表がある
この六面サイコロを使ってランダムな配置のトーナメント表を作る場合を想定する。
サイコロを8回以下の回数振って、確実にトーナメント表を作る手段はあるか?
無理やろ
全組み合わせは8!通り、“合同な”ものを同一視しても8!/128通りで7の倍数になるので無理
三角形ABCと三角形PQRが、この点の順で相似のとき
sinA = sinP
cosA = cosP
であることは明らかとしてよいですか
出た目の文字列が6^8個あるからそれぞれに選手の並びの仕方8!を対応させればいい
8!=40320<46656=6^6 だから6回でも行ける
ダブりを除けばもっと減らせる
間違えた 撤回
対応から外れた目が出た時にノーカンでやり直すと回数制限を超える
互いに割り切れない三つの自然数 a, b, c, の最大公約数が1のとき、
3整数 a+b+c, ab+bc+ca, abc, の最大公約数を求めよ。
また、3整数 a+b+c, a^2+b^2+c^2, a^3+b^3+c^3, の最大公約数も求めよ。
四分位数の問題なのだが、データ数が2つもしくは3つの場合はどのように第一四分位数や第三を出すのだろうか?
例えば、小さい順に 1,2,3 という3つのデータがあったとする
この場合2を中央値(第二四分位数)となるけれど、
第一を求めるときに 単純に最小値1と中央値2の平均でいいのだろうか
(同様に第三四分位数を求めるときに中央値と最大値3の平均でいいのだろうか)
その場合、 1,1.5,2,2.5,3と一応は4分割されているがよくわからん
同様に2つのデータの場合、例えば1,2という2つのデータがあったとする
この場合は中央値(第二四分位数)は1.5となり、1,1.5,2となるが
第一四分位数や第三四分位数は上と同様中央値で計算していいのだろうか
結果として 1,1.25,1.5,1.75,2となり、0.25で4分割はされているが
三角関数は独立変数に内角θ、従属変数が三角比と思っていたのですが、
単位円の座標平面に描かれた三角形の場合、角度θが内角になるのは第一象限だけなんですね。
直角三角形として理解するのは厳密には間違いなんでしょうか。
>>219 高校の教科書に載ってるやろ
Q₁=小さい方半分の中央値、データの数が奇数なら小さい方半分とは真ん中のデータ抜いたうちの半分
1,2,3なら2以外の小さい方半分だから1だけ、これの中央値1がQ₁
0≦t<2πなる媒介変数tを用いて
x=cost+sint
y=cost+sin2t
で表される曲線Cについて、以下の問いに答えよ。
(1)yの取りうる値の範囲を求めよ。
(2)Cで囲まれる領域の面積を求めよ。
>>221 ワイのもってる参考書にはデータ値を小さな順に並べた時そのデータを4等分する位置の値を四分位数といい、小さいほうからQ1、Q2、Q3で表す
としか書いてないンだわ
図も中央値を説明している図と照らし合わせるとおそらくQ1やQ3がQ2を省いたセットの中央値とはわかるし、
四分位数の定義はいくつかあって、文科省での提示した定義は、
データ並べてメジアンとって、そのメジアン落として小さいほう、大きいほうのそれぞれのメジアンをQ1Q3とするだから、
俺が出した データ 1,2,3の場合のQ1Q3は
2が中央値で小さなデータ1と3がそれぞれQ1Q3
個数はそれぞれ1個の奇数個だから1と3がQ1Q3か
というよりデータ数1でその値が1、データ数1を2で割って0.5、繰り上げて1か
だから1番目のデータ数だから1か
2も同様にデータ数1でその値が2、2で割って1、1番目のデータ数だから2か
うーん
じゃあ1,2だけの場合は?中央値が1.5、
というか1と2だけならデータ数は偶数個、
こいつも中央値をとって左右のメジアンだから1と2の中央値
それぞれ1と2だから上と同様に1と2がQ1Q2か
自分で書いてて理解したわ
つまり中央値の求め方がワイ適当だったんだわ
あと四分位数の定義(ここでは高校や中学の教科書に載ってる定義においての四分位数)も曖昧やった
これ中央値しっかりやらんとだめやな
しっかりもなにも定義通りに解釈するしかない。
参考書はどうかしらんが、教科書には中央値の定義として
「大きさの順にならべて中央にあるデータの値。データが
偶数個ある場合は中央に2つあるのでその平均値」と書いてあるよ。
tan1、tan4、tan7 の大小関係を調べよ。
という問いがあったら角度は狐度法なんでしょうか
π/4 < 1 <π/2 より tan 1 > 1
π < 4 < 3π/2 より tan 4 < 0
2π < 7 < (2+1/4)π より 0< tan 7 <1
よって、
tan 4< tan 7 < tan 1
sin(θ+π) = -sin(θ)
cos(θ+π) = -cos(θ)
tan(θ+π) = tan(θ)
という公式はよく掲載されてますが、なぜ次のようには書かれていないのでしょうか。いずれも、180度だけ動径を回転させる意味なので等式は成り立つはずです。
sin(θ±π) = -sin(θ)
cos(θ±π) = -cos(θ)
tan(θ±π) = tan(θ)
>>232 でも、元の式を見ても、さっきの別の表現に至るのは自明だとは思えないのですが。
教科書には記載されるべきではないかと思います、
θ-πを一回転させたらθ+πになるわけですからこれらは同じ角度を表しています
>>229 × π < 4 < 3π/2 より tan 4 < 0
○ 0< 7- 2π < 4 - π < 1 <π/2 より tan(7)=tan(7-2π)<tan(4)=tan(4-π) < tan(1)
何考えてんだよw
>>234 ×これらは同じ角度を表しています
○これらは同じ角を表しています
sin1,sin2,sin3,sin4の大小を比較せよ。
xy平面上の曲線C上の点(x,y)は、0≦t<2πの範囲を動く媒介変数tを用いて
x=sin(t)cos(2t)
y=cos(t)sin(2t)
と表される。
(1)このときxの取りうる値の範囲は( ア )、yの取りうる値の範囲は( イ )、dy/dxの取りうる値の範囲は( ウ )である。
(2)Cが閉曲線でないことの証明を解答欄( エ )に書け。
以下の2式を同時に満たすxの関数f(x)を求めよ。
f(x)=xf'(x)
f(x^2)=(x^3)f'(x)
AB=a,AD=bの長方形ABCDの対角線ACに、点B,Dからそれぞれ垂線を下ろし、その足をH,Iとする。
H,Iを通りADに接する円の半径をa,bで表せ。
y = xy' → ∃A( y = Ax (∀x>0) ) → ⊥
2^n+3^n=100n^2
を満たす正整数nが存在するならばすべて求めよ。
自作爺さんの発狂ぶりが酷いな > ID:I+BVBBEa
爺さんの発狂ぶりを讃えて、みなさんでご唱和ください。
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
a[1]=1
a[n+1]=p*a[n]+1/6
である数列{a[n]}を考える。
lim[n→∞] a[n]が収束するような実数pの範囲を求めよ。
>>246 「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
半径1の円がある。
これに接するように正方形(の枠) Sがある。
この時、この正方形Sの中に
六角形を入れて回転させると…どこにも引っかからずに回転ができた。
このような条件をみたす六角形R_nのうち、
面積が最大となるものをR_0とする。
六角形 R_0 の6つの角度を求めて、
その六角形を図示せよ。(正六角形とは限らない)
円に内接する6角形のうち最大面積のものを求めろ、って問題じゃないのか?
流石に円じゃなくて正方形にぶつからないだとは思うけどこんな簡単な問題設定ひとつ他人に説明できない時点でこの板に来る資格ないやろ
>>250 それだと正六角形で一発で答えにたどり着くやんけ。
そうじゃなくて、四角い枠の中で回転可能かどうかだ。
答えがわかれば、食器の形状として合理的だって分かるだろ。
食器棚を圧迫せずにそれなりの大きさの器として使えるからな。
正六角形もまぁ合理的だし食器棚に入れるのに
悪くはないんだが、つまらんからな。
>>251 どういうアプローチで解くのか、
251選手の書き込みに注目があつまりますねぇ。
ち、ちなみに謙虚な神戸大卒 TOEIC700です…( ; ‘ω‘) ハァハァ
>>249 傑作認定します
解いてくださいますようお願い申し上げます
>>246 簡単そうに見えて意外と難物です
傑作なのでよろしくお願い申し上げます
このIDでは9レス目ですので9にちなんだ問題を質問します
9桁の平方数で最小のものと最大のものを求めよ。
>>253-254 手と頭を働かせて!
少しは自分で考えて!
あとは
>>251選手の模範解答に期待やね ( '‘ω‘)
このIDで10レス目です
直径1の円に内接する正十角形の周長をLとする。
Lと3.1の大小を比較せよ。
p=1とき明らかにダメ
p≠1のとき b[n]=a[n]-1/(6(1-p)) と置くと等比だから絶対値が1未満で収束
10^8≦9桁の数<10^9 10^4≦√(9桁の数)<10^4√10 最小が1万 最大が31622
正n角形の周の一つの線分の長さの半分はsin(2π/n/2)だから半周長はnsin(π/n)
sin(π/n)>π/n-(π/n)^3/6 半周長<π-π^3/n^2/6<3.15-3.14^3/n^2/6<3.1
3^n-2^n=1
をみたす正整数nを全て求めよ。
>>252 まあね。
いったいなんのために問題設定に円を持ち出したのかがわからんのよ。
正方形の内部で、中心移動しても、接点をすべらせてもよいので
360°回転可能な六角形のうち最大の面積のものを求めよ、
ってことなんだろうな。
6角形でなく、三角形であれば正方形の辺長と同じ辺長の正三角形だろうけど、
四角形以上の多角形だと内接円に内接する正多角形になるのか?
>>259 1∈R、a=a1∈(a)
a∈I、r∈R⇒ra∈Iより(a)⊂I
(a)=R⇒∃r∈R、ra=1⇔a∈R×
逆にa∈R×ならば∀a、1=a⁻¹a=1が成り立つので(a)=R。
>>257 a∈(a)⊂(b)は(1)から分かる
a∈(b)⇒(a)⊂(b)は(2)から分かる
∃c、c∈R、a=bc⇒a∈(b)
>>255 b=0の時は成り立つ
b≠0の時、a=bu、b=avより
uv=1、u∈R×
先生教えて
9種類の中からランダムで5個選ぶのを7回やったとき
全種類ゲットできる確率はなんぼですか?
>>264 この質問に答えたら答えてあげます
lim[n→∞] [e-{Σ[k=0,n] 1/k!}]n^t
が0でない定数に収束するような実数tを求めよ。
1-₉C₄(4/9)³⁵+₉C₃(3/9)³⁵-₉C₂(2/9)³⁵+₉C₁(1/9)³⁵
a,bは正の実数とする。
ax^2+bx^2≦1で表される領域の内部の点(s,t)を(X,Y)=(s+t,st)に移すとき、移った先の領域をXY平面上に図示せよ。
>>254 Rを体としIをRのイデアルとする
(a)⊂Iが成り立ち、a∈R×が成り立つ
定数項a₀=0である多項式から成る環は単項イデアルではない。
>>260 ああ、ごめんよ。
「円に内接するような形状」っていうのと「正方形の内側で回転可能な形状」
って点、この2点の違いを明確にしたかったんや。
円に内接するだけならば「円の内側で回転可能 = 正N角形」
って同値だけどさ、今回は違う。
「正方形の内側で回転ができるようなデカい多角形」 っていう条件だから
そうなると…正N角形とは限らないよねって話。
N=3や4 では この2つを満たす多角形は
同一の正N角形になっているけど、あくまで、たまたまそうなるだけ。
N=6、 六角形で考えると
求めていけば正六角形よりデカい形状の六角形が得られる。
>>269 ルーローの三角形 (ギターのピックみたいな) ならぬ
ルーローの六角形ってところだぁね。
連立方程式
x+y+z=3
xy+yz+zx=3
x^2+y^2+z^2=3
を解け。
>>272 実数解の1つはすぐ見えると思います
問題は残りの2解で、複素数を絡めた深遠な理論が背景にあります
よろしくお願い申し上げます
>>269 >N=3や4 では この2つを満たす多角形は
>同一の正N角形になっているけど、あくまで、たまたまそうなるだけ。
同一の正N角形、ってどういう意味?
>>272 x^2+y^2+z^2=(x+y+z)^2-2(xy+yz+zx)=3
つまり
1行目&2行目→3行目
となるためこれは不定方程式です
連立方程式
x+y+z=3
xy+yz+zx=3
x^3+y^3+z^3=3
を解け。
>>275 重要な示唆をありがとうございます
質問を変更しました
つまりは自分で解答用意してない問題貼り付けてるわけだ
e^x=Σ[k=0,n-1]x^k/k!+x^n/n!e^(θx) ただし0<θ<1
e-Σ[k=0,n-1]1/k!=e^θ/n!=e^θ/{√(2π)n^(n+1/2)e^(-n+φ/(12n))}但し0<φ<1
{e-Σ[k=0,n-1]1/k!}n^t=e^(θ-φ/(12n))/√(2π)*{n^(-n-1/2+t)e^n}→0 解なし
>>276 実数解は明らかですが複素数領域にまで踏み込んだらどうなるか?
良問です
I = ∫[0,1] 1/(1+x^2) dx
J= ∫[0,1] 1/{1+(1-x)^2} dx
に対して、I+Jを求めよ。
>>280 おまえのための歌だ。
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>280 良い歌です
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>280 自画自賛する自作爺さんに捧げます
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
前
>>196 >>264 {1-(4/9)^7}×100=99.65745126……(%)
∴99.65745126%以上の確率で全種類ゲットできる。
前
>>285 >>272 x+y+z=3
xy+yz+zx=3だから、
x^2+y^2+z^2=(x+y+z)^2-2(xy+yz+zx)=3^2-2・3=3
∴x=y=z=1
>>280 この問題が問題になどなってない事がわからない無能
>>249 あれ、調子こいてたら
解き方ど忘れしたわ。
今から解き直すか…あーしんど ( '‘ω‘)
>>251選手が模範解答でも
書いてくれたらいいのになぁ
N=4.
(2/3,0)-(0,2/3)-(-4/3,0)-(0,-4/3)-(2/3,0).
そもそもルーローの三角形は三角形ではない
じゃあ“ルーローの六角形”と言ってる奴も六角形じゃないんやろ
だつたらなにと聞こうと思ってやめた
時間の無駄
>>252 食器棚の中で皿を回転してる人想像したら怖くなったから止めた
誰か、3元3次以下の対称式、交代式に関するこれぞ良問という良問を投げておくれ
|z-4-4i|=2√2 を満たす複素数zで
z^2021 が純虚数となるようなものはいくつあるか。
という問題は、zを極形式で考えるでしょうか?
>>293 そうです
偏角θの2021倍が±π/2なので
θ=(2n+1)π/4042
|z-(4+4i)|=2√2は4+4i中心半径2√2の円なので
π/4-π/6=π/12≦θ≦π/4+π/6=7π/12
π/12≦(2n+1)π/4042≦7π/12
4042/12=2021/6≦2n+1≦7・4042/12=7・2021/6
2021≦2022=12・168+6≦12n+6≦12・1178+6=14142≦7・2021=14147
(2n+1)π/4042=π/12, 7π/12は無いので2倍
よって
2・(1178-167)=2022個
あら綺麗ね
おおよそ半分が奇数だから
2・(7・4042/12-4042/12)/2=2021~2022個か
大人になっても漫画アニメゲームおもちゃロリアイドル宗教に
はまってる人は知恵遅れのガイジみたいなもの
高機能自閉症や発達障害だと思ってまず間違いない
コミケなんてのは知恵遅れのガイジが集まる運動会みたいなもの
アスペルガー症候群と高機能自閉症
「反復運動」と「限定された物事へのこだわり・興味」
3つの診断基準
①人とのやり取り、関わりが難しい(社会性の障害)
②コミュニケーションがとりにくい(コミュニケーションの障害)
③興味・行動の偏り、こだわり(限定的な行動・興味・反復行動)
ASD(自閉スペクトラム症、アスペルガー症候群)の症状
細部にとらわれてしまい、最後まで物事を遂行することが出来ない
視線があいにくく、表情が乏しい、感覚の偏り、運動のぎこちなさ、
切り替えが苦手、決まったパターンと違うと癇癪を起こす、
集団での活動・遊びが苦手。
考え方や行動に融通がきかず、興味の対象が狭い範囲のものごとに限られる、
全体像を把握することが苦手、記憶することは得意だが、想像するのは苦手
>>286 イナさんは統計学とか興味ないですか?
データサイエンティストが勉強しているよね
統計検定もあります
少しネットを離れていました。
私の良質な質問が待ち遠しかったですか?
【質問】
lim[x→∞] {e-(1+1/x)^x}x^r
が0でない定数に収束するような実数rを求めよ。
>>294 あのすみません。π/4+π/6 は5π/12になりませんか。
tが正のとき log(1+t)=t-at^2 1/a=2(1+θt)^2 ただし0<θ<1
(1+t)^(1/t)=exp(1-at)=e*e^(-at)=e*(1-at+bt^2)但し b=a^2/2e^c 0<c<at
{e-(1+t)^(1/t)}t^-r=e(at-bt^2)/t^r=eat^(1-r)-ebt^(2-r)
r<1のとき 右辺→0(t→0) r>1のとき 右辺→∞(t→0) r=1のとき右辺→ea=e/2
>>292 すみません因数分解の質問があります。丁度そこに当てはまる質問かも知れません。
x^3 +Y^3 +z^3 + 3(y+z)(z+x)(x+y)= (x+y+Z)^3
の因数分解を、なるべく手計算せず見通しよく一発で
証明する方法はないでしょうか
>>300 コレは?
f(x) = x^3 +y^3 +z^3 + 3(y+z)(z+x)(x+y)
≡ x^3 +y^3 +z^3 - 3xyz
≡ 0 ( mod ( x+y+z ) )
f'(x) = 3x² + 3(y+z)(2x +y + z)
≡ 3x² - 3x x
= 0 ( mod ( x+y+z ) )
f''(x) = 6x + 6(y+z) ≡ 0 ( mod ( x+y+z ) )
>>302 なかなか面白そうな証明有難うございます。
本当に面白いと思いました。
ただ、2つ目の「≡」を示すにはネット上で有名なあのちょっと面倒な因数分解を
経由しないといけないかもなのが若干しんどいので惜しいです
>>297 Rを可換環、Iをそのイデアルとする。
I≠R、ab∈I⇒a∈Iまたはb∈I
の2つの条件が成り立つ時、Iを素イデアルと言う。
RのイデアルJに対して
I≠R、I⊂J⇒J=IまたはJ=R
の2つの条件が成り立つ時、Iを極大イデアルと言う。
>>303 ネット上で有名って
x³+y³+z³-3xyz = (x+y+z)(x²+y²+z²-xy-yz-zx)
は普通に高1で習う因数分解の公式だけど
じゃあ
f(-y-z) = y³ + z³ - (y+z)³ + 3yz(y + z) = 0
コレも
a³+b³ = (a+b)³ -3ab(a+b)
で高1で習うし
>>303 自己レス訂正
modで0を示すだけなら、2つ目の「≡」も言うほどには別に
ゴチャゴチャしていませんが、しかし全体としてステップが3つになってしまう
ところが惜しいけれど残念です
>>281 a∈Rが定める、Iに関する合同類をxとするとa∈I⇔x=0
f:a∈J→a+I∈R/I
g:a+I∈J'→a∈J
とする。これらの間には自然な一対一対応がある(互いに逆写像)。
x+y=t xy=u と置く
x^3 +Y^3 +z^3 + 3(y+z)(z+x)(x+y)
=t^3-3tu+z^3+3t(z^2+tz+u)
=t^3+z^3+3tz(z+t)=(t+z)^3
x³+y³+z³+3(x+y)(y+z)(z+z)
= p(x+y+z)³+q(x+y+z)(xy+yz+zx)+rxyz
f'(-y-z)
= q(-(y+z)²+yz) + ryz
よりq=r=0なら1発
>>280 I₁∪I₂⊂I₁+I₂である。
一般にはI₁∪I₂はイデアルではない。
積I₁I₂は∑abによって定義されることに注意する。abではない。
>>277 ab∈I₁、ab∈I₂
b∈I₂⊂Rよりab⊂I₁
a∈I₁⊂Rよりab⊂I₂
整数環Z
I₁+I₂=gZ、I₁∩I₂=lZ、I₁I₂=mnZ
和、共通部分、積。
a≡b modI⇔a-b∈I
>>276 合同類。剰余類。
Rの中のIを法とする合同類全体を集めたものがR/I。aj+I、aj'。
ab≡cd
ab-cd=ab-ad+ad-cd
=a(b-d)+(a-c)d≡0
(adかbcを+-する)
これは両側いの性質を使っている。実際行列環によって左イデアルでは成り立たないことが分かる。
合同類の代表元の取り方によらず一意的に演算が定まる。
>>273 剰余環。商環。Z/mZは剰余環の記号を用いているということ。
R/{0}=R、R/R={0}=零環。
R[T]/(T)=Rである。
R[T]/(T²+1)=Cである。
>>309 これもスタンダードな良い別の視点ですね。解答有難うございます。
>>310 これまた大変面白そうな興味深そうな証明ですが恥ずかしながら
私が式変形についていけてませんorz
・1つ目の等号が何故そう置ける事が保証されるのか
・f'(-y-z)が何故恒等的にゼロなのか
因みに私自身が考えた地味な証明は
x^3 +y^3 +z^3 + 3(y+z)(z+x)(x+y)をxの多項式として整理すると
x^3 +3(y+z)x^2 +3((y+z)^2)x +y^3 +z^3 +3yz(y+z)
=x^3 +3(y+z)x^2 +3(y+z)^2x +(y+z)^3
=(x+(y+z))^3
ですが、何も迂回しない最もストレートで標準的な証明ではあるでしょうが
ゴリゴリ地味過ぎて、そこそこゴチャゴチャしていますし何より
元の式の簡明さの秘密そのものを全く解き明かしていない気がしてます
(x+y+z)^3=(x+y+z)(x+y+z)(x+y+z)
というのは3つの括弧の中から一つずつ文字を選んで掛け合わせて
合計3^3=27個の単項式を生成しますが、x^3, y^3, z^3を
除いた残り24個の単項式については
x+(y+z), y+(z+x), z+(x+y)について対称性でひねれば
丁度3(y+z)(z+x)(x+y)が一発で出てきそうなのですが
詳細が分かりませんorz
すみません元の問題が何かについて見やすいように
>>300を一応再投稿させて頂きますすみませんm(_ _)m:
x^3 +Y^3 +z^3 + 3(y+z)(z+x)(x+y)= (x+y+Z)^3
の因数分解を、なるべく手計算せず見通しよく一発で
証明する方法はないでしょうか
>>315 対称式は基本対称式の多項式として表すことができるという性質があります。
これの証明は高校ではやらないけれど、基本性質として覚えておいて損はないです。
単に、t=x+y+z、s=yz+zx+xy、r=xyzとおくと、x、y、zに関する対称式はt、s、rの多項式として表されるという形式的な性質を利用するだけなので。
そうすると、t、s、rを徹底的に利用することで、次のような式変形が。
x^3+y^3+z^3=3xyz+(x+y+z)(x^2+y^2+z^2-yz-zx-xy)=3xyz+(x+y+z){(x+y+z)^2-3(yz+zx+xy)}=3r+t^3-3ts 。
x+y=t-z、y+z=t-x、z+x=t-y から (x+y)(y+z)(z+x)=(t-z)(t-x)(t-y)=t^3-(x+y+z)t^2+(yz+zx+xy)t-xyz=t^3-t*t^2+st-r=ts-r
以上から
x^3+y^3+z^3+3(x+y)(y+z)(z+x)=3r+t^3-3ts+3(ts-r)=t^3=(x+y+z)^3
>>317 それと、
>>317で使っている例の3次の有名因数分解の式変形は
f(U)=(U-x)(U-y)(U-z)=U^3-tU^2+sU-r とおけば f(x)=f(y)=f(z)=0 なので
x^3-tx^2+sx-r=0
y^3-ty^2+sy-r=0
z^3-tz^2+sz-r=0
3式を辺々加えると
x^3+y^3+z^3-t(x^2+y^2+z^2)+s(x+y+z)-3r=0
すなわち
x^3+y^3+z^3-t(x^2+y^2+z^2)+(xy+yz+zx)t-3xyz=0
これより
x^3+y^3+z^3-3xyz=t(x^2+y^2+z^2-xy-yz-zx)=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)
出題者は多分組み合わせ論系の想定解持っててそれを披露したいんじゃないかな
なのでそれ系の解答が出てくるまでは何が出てきてもダメだって言われるだけだよ
すみません
昨日も忙しく質問を投稿できませんでした
(1)から意外と難しいです
【質問】
(1) 不定積分 ∫ 1/(xlog(x)) dx を求めよ。
(2) r>1とする。
lim[n→∞ ] Σ[k=1,n] 1/k^r
は収束することを示せ。
(3) lim[n→∞] Σ[k=2,n] 1/(klog(k))
は収束するか。
>>319 なるほど、なるほど。
どんな種明かしか、楽しみだ。
与式=∫e^-t/t*e^tdt=log│t│+C=log│logx│+C ただしt=logx
減少だから Σ[k=2,n] 1/k^r<∫[1,n]dx/x^-r=(1-n^(1-r))/(r-1)→1/(r-1) (n→∞)
増加だから Σ[k=2,n] 1/(klog(k))>∫[2,n]dx/(xlogx)=log│logn│-log(-log2)→∞
>>317 >対称式は基本対称式の多項式として表すことができるという性質があります。
なるほど!噂には聞いたことありますが、それを使えば、x, y, zの次数に
着目すれば、以下の式が自然に立式可能な訳ですね
x³+y³+z³+3(x+y)(y+z)(z+z)
= p(x+y+z)³+q(x+y+z)(xy+yz+zx)+rxyz
あとf'(-y-z)が何故恒等的にゼロなのかはまだ分かりません
因みに貴方が丁寧に書いて下さった式変形は大変恐縮なのですが
私自身の地味な証明より遥かに手計算の量が増えているので、目では追えません
>>319 >出題者は多分組み合わせ論系の想定解持っててそれを披露したいんじゃないかな
そんなツマラナイ趣味は私にはないです
私自身の地味な力ずくの証明より手計算の量が少なく見通しが良ければ
どんな方法でも何でもいいです
私はただ『すんなり』と『理解がしたい』本当それだけです
組合わせに特別興味ある訳でもなく出題の競い合い力比べにも無関心です
>>302はあくまで別解としてとても興味深く面白い方法ですが
x^3 +Y^3 +z^3 + 3(y+z)(z+x)(x+y)= (x+y+z)^3
の『自然』な理解の仕方としては、私自身の方法を現時点で採用せざる得ません
>>249 に誰か答えろよ。
おまえら、ホイ卒か幼卒ですか?
色の塗り分け問題の質問です
3色のペンキを使って、隣り合う正方形同士が異なる色となるように塗っていきます
その塗り方は何通りありますか?
2015年のセンター数学1A 第4問のイメージなのですが、
横X列の場合ではなく、横X列・縦Y列の場合となった時、それを求める公式はありますか?
>>326 早速ありがとうございます
大変お手数かけますが、どういった計算になるか教えていただけないでしょうか。。
具体的に、
横2列・縦2列
横4列・縦3列
ですと、どのような式になりますか?
>>325 こういうのは再帰的な処理、繰り返しの典型的な問題だな。
で、こういう反復系のものは
数学で言うところの漸化式ってやつで表現できる。
複雑で理解しづらいような大きな問題は
理解しやすい小さな問題へ置き換えて考えろ。
問. 2x2 で式を立てよ。
3x3 で式を立てよ。
4x4 で式を立てよ。
↑ここまで解けたか? ここまで来ればもうあとは分かるだろ?
NxN で式を立てよ。
お分かりいただけただろうか?
むっけぇ問題はちっちぇえ問題に分割して置き換えたら解きやすい。
これ、大人の知恵な ( '‘ω‘)
lim[n→∞] (1/n){√P[2n,n]}
を求めよ。
3^n-2^k=1を満たす正整数の組(n,k)をすべて求めよ。
cos1,sin1,cos2,sin2,cos3,sin3,cos4,sin4
を小さい順に並べよ。
>>329 ありがとうございます
なるほど!意味がわかりました
三角関数の加法定理によって余角の恒等式が導けるらしいのですが、
tan(90°)の場合、未定義か無限大になってしまってどう解いたらいいのか分かりません。
tan(90°-θ) = \frac{tan(90°)-tan(θ)}{1+tan(90°)tan(θ)}
= ?
(>ω<)
次の2式をともに満たす複素数xの値を全て求めよ。
x^3-2x+1=0
x^4-2x+1=0
x^3-2x+1=0
x^4-2x+1=0
⇆
x^3-2x+1=0
x^4-x^3=0
⇆
x^3-2x+1=0
x=0,1
⇆
x=1
>>336 tanの加法定理だけで押すなら、たとえばこんな感じか?
tan(π/2 -θ)
=tan(π/4 +(π/4-θ )
={1+tan(π/4-θ)}/{1- tan(π/4 -θ)}
={ 1+{1-tanθ)/(1+tanθ)}/{1-(1-tanθ)/(1+tanθ)}
={(1+tanθ+1-tanθ)/(1+tanθ)}/{(1+tanθ-1+tanθ)/(1+tanθ)}
=1/tanθ
=cotθ
そんなややこしいことしなくても定義に立ち戻って、
tan(π/2-θ)=sin(π/2-θ)/cos(π/2-θ) =cosθ/sinθ=cotθ
>>341 私は常にスレの数学力を上げる質問をしています
感謝してください
23x-19y=1
を満たす整数(x,y)のうち、|x^2+y^2|を最小にするものを求めよ。
>>344 互除法を用いて式変形していくと,
〈1段階目〉
23x - 19y = 1
19(x-y) + 4x = 1
〈2段階目〉
16(x-y) + 4x + 3(x-y) = 1
4(5x-4y) + 3(x-y) = 1
〈3段階目〉
3(5x-4y) + 3(x-y) + (5x-4y) = 1
3(6x-5y) + (5x-4y) = 1
この状態なら解の例は簡単に出て,
6x-5y = 0
5x-4y = 1
を解いて,
x=5, y=6 が,この不定方程式の解の例ですね。当然,
23×5 - 19×6 = 1
なので,問題文の式からこれを引くと,
23(x-5) - 19(y-6) = 0
23と19が互いに素であることに注意して,
(x-5) = 19t
(y-6) = 23t
但し t∈?
なので,
x = 19t + 5
y = 23t + 6
最小化したいのは |x|2+|y|2 ですけれど,
(x,y)=(5,6)の前後は|x|も|y|も増える一方なので,
(5,6) が答えだと思います。
ごめんなさい,化けていましたね。
tは整数で,?になっている物は,黒板太字のZです。
すみませんが、教えていただけないでしょうか。
nを正の整数とする。等式
Σ[k=0,n] C[n-k.k] = 1/√5 { ((1+√5)/2)^(n+1) - ((1-√5)/2)^(n+1) }
が成り立つことを示せ。ただし、n-k < k のとき C[n-k,k] = 0 とする。
>>349 前提知識として, C[n,r] + C[n,r+1] = C[n+1,r+1] です。
左辺の式を S_n とします。
S_n + S_{n+1}
= (C[n,0] + C[n-1,1] + … + C[0,n])
+ (C[n+1,0] + C[n,1] + … + C[0,n+1])
= C[n+1,0] + (C[n,0]+C[n,1]) + … +(C[0,n]+C[0,n+1])
= C[n+2,0] + C[n+1,1] + … + C[1,n+1] + C[0,n+2]
= S_{n+2}
※ C[n+1,0] = 1 = C[n+2,0]
※ C[0,n+2] = 0 なので勝手に付け足しています。
あとは初項を求めると,S_nはフィボナッチ数列であることが分かるので
三項間漸化式の解き方を用いると右辺になります(自信ない)
>>344 Φ:R₁→R₂、R₁、R₂は環、Φは写像
Φ(a+b)=Φ(a)+Φ(b)
φ(ab)=φ(a)φ(b)
φ(1₁)=1₂
が成り立つ時、写像φを環準同型と言う。
>>345 コテハンで自作爺さんにレスする馬鹿はイナさんだけかと思ったがwww
ご褒美に一曲進呈しよう。素晴らしい歌だよ。
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>350 なるほど!証明できそうな気がしてきました。
ありがとうございます!!
>>342さん、イカしてます。😃
ありがとうございました。🍜ラーメンどうぞ。
>>343 φ:R→{0}は環準同型
包含写像i:R₁→R₂は環準同型
i(a)=a
φ:R→R/I、Z→Z/mZ
射影pr:R→R₁、R→R₂は環準同型
tを実数の定数とする。xの方程式
x^2-(t^2)x+t^4=0
が持つ実数解の個数を調べよ。
n≧3,k≧2とする。
C[n,k]+C[n,k+1]はどのような正整数pの倍数にもなれるか。
k=n-1のとき
C[n,k]+C[n,k+1] = n + 1
>>358 素晴らしい
よくトラップをかいくぐりましたね
前
>>286 >>356 x^2-(t^2)x+t^4=0
D=t^4-4t^4=-3t^4≦0
∴解の個数は、
t=0のとき1個
t≠0のとき0個
私は名作質問を作ります。
lim[n→∞] (1/n)√P[2n,n] を求めよ。
(1966 東工大)
>>360
違うよ。嘘つき自作爺さん= ID:agIHH0l+ のスレだよ。
参加者はこれを歌う義務がある。
↓
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪ どのような質問なら数学力を高められるのか興味があります。
そのような質問をしてください。
>>365 質問です!
自作爺さんはどこで数学の勉強をされたんですか?
私も数学力を高めるために自作爺さんの跡を辿りたいと切に願っています。
大学と大学院名を教えて下さい。
>>366 はい。
東京大学教養学部在籍中です。
理科一類で入学しました。
教養溢れる質問をします
a,b,c,dを実数とする。
xy平面上の3直線
y=ax
y=bx
y=cx+d
について、以下の問いに答えよ。
(1)どの2直線も平行でないとき、a,b,c,dが満たすべき条件を述べよ。
(2)(1)の条件を満たすとき、この3直線がなす三角形の面積をa,b,c,dで表せ。
この質問に答えられない奴は馬鹿です
x^n-x+1=0を満たすn個の複素数は、いずれも絶対値が1でないことを示せ。
x^2-x+1=0はx=(1±√3i)/2を解に持ちますね
わざと間違った問題出してレスつけてもらうレス乞食化したな
>>372 ならば>368の誤りもわかりますよね?
>>374 虚しいなどありえません
私の中から情熱が溢れてくるので、1質問をするのに3分とかかりません
>>367 そのお歳で大学生とは感心しました。あなたを称える歌を捧げますので、
孫と同じような年齢の御学友と一緒にカラオケで歌って盛り上がってください!
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
|(a(-1)d-(-1)bd)^2/(2(a(-1)-(-1)b)(a(-1)-(-1)c)(b(-1)-(-1)c))|
=|(a-b)d^2/(2(a-c)(b-c))|.
nを正整数とする。
x^n+y^(2n)=z^(4n)
を満たす正整数(x,y,z)は存在しないことを示せ。
a,bを正整数とする。
(1/a)+(1/2b)+(1/ab)=1
を満たす
Σ[k=1,n] (C[n,k])/{n^2*(n+1)!}
をnで表せ。
>>381 と、昭和脳丸出しの自作爺さんにいわれても、
こう返すしかないわ。
↓
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
爺さんって何歳からですか?
ちなみに40歳のこど叔父です ( '‘ω‘)
前
>>361自習。
∫[θ=0→π/2]{sinθ/(sinθ+cosθ)}dθ
=∫[θ=0→π/2]{(sinθcosθ-sin^2θ)/(cos^2θ-sin^2θ)}dθ
=∫[θ=0→π/2][{sin2θ/2-(1-cos2θ)/2}/cos^2θ]dθ
=∫[θ=0→π/2](sin2θ/2cos2θ-1/2cos2θ+1/2)dθ
=?-?+[θ/2](θ=π/2)
=?+π/4
=π/4
私はこのスレを学びの場にしたいのです
出題はしていません
学びの得られる質問をしているだけです
基礎学力0やん
リアルワールドで数学の勉強するのが先やろ
∫[0,∞] {sin(x)}/x^2 dx
を求めよ。
>>389 定番の積分に一捻りを加えるだけでこのような大傑作となります。
秒で答えを出してください。
>>388
俺の母校をお前の嘘で穢さないでくれよ、自作爺さん。
お前にはこの歌がやっぱりふさわしい。
↓
「自作」(与作の節で)
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪ >>391 その方は歌にもなってる有名人であらせられるぞ
まさか知らぬとは言わせん
↓
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
私の質問は皆様の数覚を格段に引き上げます
【傑作質問】
3辺の長さがそれぞれ
a+2b,b+2c,c+3a
であるような三角形が存在するとき、実数a,b,cが満たすべき関係を求めよ。
何かの本に、 いくつかの実数で f(x)>0
が成立しているなら、
xf(x) - f(f(x)) / f(x) は∞になるとありましたが、何を言ってるか分からないし
なんでこういう分かりにくいことを平気で言うのか分からないので教えてください
>>383 >>386 こういう若手の老害って
ほんまウザいよな。 おれだけど( '‘ω‘)
>>396 君さあ、具体例代入するくらいの頭もないわけ?
>>399
説明できないからそういう反応になるんだろ ゴミ
理解できるなら普通に説明してみろよバカ >>402 君何か勘違いしてるみたいだけど、質問すれば答えてもらえるわけじゃないのよ
MARCHか理科大あたりのうだつの上がらない理系に答えてもらいなよw
実社会で働いてるわけでもなく インターネットの匿名掲示板 2ちゃんねるに
いるくせに、 説明できない
完全に終わってるなお前
実数a,bはa^2+b^2+|ab|≦4を満たす。
x,yが-1≦x≦1かつ-1≦y≦1を動くとき、ax+byの取りうる値の範囲を求めよ。
sin1,cos1,sin2,cos2,sin3,cos3,sin4,cos4
を小さい順に並べよ。
>>403 自作は東大生(自称)♪
どあほー、どあほー♪
駒場にかえるとさー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンキン大、トンキン大♪
先輩だよイナさん♪
トンキン大、トンキン大♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
a,bは複素数の定数とする。
方程式ax^2+bx+1=0の解をa,bで表せ。
>>410 数学力の基礎を鋭く問う傑作質問です
よろしくお願いいたします
f(x) = (∫[0,1] f(x) dx)x^2+(∫[0,1] f'(x) dx)x+1
を満たすf(x)を求めよ。
>>385 A=∫[θ=0→π/2]{sinθ/(sinθ+cosθ)}dθ
=∫[θ=0→π/2]{cos(π/2-θ)/(cos(π/2-θ)+siin(π/2-θ))}dθ
=∫[θ=0→π/2]{cosθ/(sinθ+cosθ)}dθ
A+A=∫[θ=0→π/2]{1}dθ=π/2
f(x) = (∫[0,1] f(x) dx)x^2+(∫[0,1] f'(x) dx)x+1
f(0)=1
f(1)= ∫[0,1] f(x) dx+f(1)-f(0)+1 ∫[0,1] f(x) dx=0
f(x)=0*x^2+(f(1)-f(0))x+1=(f(1)-1)x+1
∫[0,1] f(x) dx=(f(1)-1)/2+1=f(1)/2+1/2=0 f(1)=-1
f(x)=(-1-1)x+1=-2x+1
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
私の質問は不要ですか?
不要ならばこのスレから去ろうと思いますが
前
>>385 >>395 a+2b+b+2c-(c+3a)=3b+c-2a>0
b+2c+c+3a-(a+2b)=3c+2a-b>0
c+3a+a+2b-(b+2c)=4a+b-c>0
2b+4c>0
6a+2c>0
2a+4b>0
8a+6b+6c>0
4a+3b+3c>0
b+2c>0
3a+c>0
a+2b>0
3a+b+3c>0
4a+2b+c>0
a+3b+2c>0
7a+3b+4c>0
5a+5b+3c>0
4a+4b+5c>0
>>420 なるほど、では面白くする努力をいたします。
よろしくお願いいたします。
>>421 面白い質問をいたします
pを実数の定数とする。
またf(x)=x^3+3x-pとする。
実数tに対してうまく複素数yをとることで、
t=y^3+3y-p
とできることを示せ。
>>425 f(x)は問題文のどこに使われていますか?
それはともあれ
複素係数の代数方程式は複素解をもつのでOK.
>>419 何スレも前から面白くないから去れ、って言わてるだろ。
さっさと去ってくれ。
>>424 >>422はお前じゃなくてイナさんを労ってんだろ。
>>425 複素数解というか、普通に実数解を持ちますね
グラフを考えれば一発ですけど
>>427 私は去ってほしくないんですよ
せっかくこのスレに勢いが出てきたのに、むしろこれを契機として盛り上がる方向で行きましょうよ
>>430 何度も同じことを指摘してるが、自作爺さんが好きなら別スレでやれよ!
高校数学とは無縁の話でほんとに盛り上がってると思うのなら、別スレ
でも盛り上がるだろ。ここでやる必要はない。
そんなことも理解できない低能だからクソ問題をありがたがるのだろうけどね。
前はそれなりに数学の問題になってるやつも出してたけど、もう答え出そうにないやつ、即答できてしまうやつ、解ないやつしか出てこない
レスつけて欲しいだけやろ
>>432 前はそれなりに数学だったって、変わってなくね?くだらない
自作爺さんの自作自演か? > ID:yE0Ih+TB
スレ違いだからよそでやれっていう当然の要求を無視して
スレを荒らし続ける自作爺さんが悪いってことは自明。
議論の余地はない。
>>435 いつも変な自作の歌をコピペしているのは荒らしだと思いますよ
コピペはスパムともいい、低レベルな荒らしです
>>436 そうなんですね
私はショートスリーパーです
私は荒らしではないですが質問します
2^100は30桁以上の整数であることを示せ。
ただしlog_10[2]などの値、評価は自身で求めること。
2^100=(2^10)^10=1024^10>(10^3)^10=10^30
『悪い奴ほどよく眠る』(わるいやつほどよくねむる)は、1960年に公開された日本映画である。監督は黒澤明で、黒澤プロダクションの第1作である。公団の汚職で死に追いやられた父の復讐を果たそうとする男の姿を描く。物語はデュマの小説『モンテ・クリスト伯』を参考にしており、シェイクスピアの戯曲『ハムレット』の影響も指摘されている。
微分可能な時f(x+2h)-f(x+h)/hはf’(x)と同値になりますか
>>微分可能な時
「fがxで微分可能な時」という意味?
>>442 なります
けど高校レベルで証明できるかは微妙ですね
いや普通に証明できますね
f(x+2h)-f(x+h)/h
=2•[f(x+2h)-f(x)]/2h-[f(x+h)-f(x)]/h
>>442 h → 0 の時,
(f(x+2h) - f(x+h))/h = [(f(x+2h) - f(x))/h] - [(f(x+h) - f(x))/h]
= 2[(f(x+2h) - f(x))/(2h)] - [(f(x+h) - f(x))/h]
→ 2f'(x) - f'(x) = f'(x)
となりますね.
f(a)-f(b)=(b-a)f'(c) a<c<b
f(x+2h)-f(x+h)=hf'(t) x+h<t<x+2h
aを負の実数とする。
以下の極限を調べよ。
lim[x→0] (a^x-1)/x
>>447 なるへそ。つまり、その結果を用いて次のように言っていいんだな。
一般に xが実数 で 関数 f(x) がxで微分可能である時、
h->0 について
f ' (x+h) = f ' (x)
↑ これが成立する
って言っちゃっていいんだな。
直観的に理解できる事実。
>>437 君を称える歌だよ。
自作爺さんの書き込み数には遠く及ばないので、荒らしにすらなってないと思うし、
自作問題よりも良く出来た替え歌なので、特に君にはよく味わって欲しい。
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>450 h->0の結果だけど?
なんで
(f(x+h+h)-f(x+h))/h
の一部のhをh->0にしなくて良いと思えるの?
>>439 1267650600228229401496703205376 で 31桁。
31>30
∴示された
>>449 高校数学と思いきや複素数の真実に迫る良問です
よろしくお願いいたします
>>454 私の質問は常にこのスレをリードしています
あなたの書き込みとは価値が、頭の良さが、違うんです
そうでないと仰るなら反論をしてください
2>125/64=(5/4)^3
10=8*(5/4)<2^(3+1/3)
log[2]10<3+1/3
log[10](2^100)=100log[10]2=100/log[2]10>100/(10/3)=30
>>459 R言語を使用
> gmp::as.bigz(2^100)
Big Integer ('bigz') :
[1] 1267650600228229401496703205376
>>458 そう思うなら、別スレでリードしまくればいいじゃないか。
高校数学の質問スレは、スレタイに見合った適切な投稿がリードすべきなんだよ。
たとえスローペースでもそれがスレのあるべき姿。あんたは荒らしてるだけ。
頭のレベルがどうのという問題ではない。
倫理観の欠如が君の最大の問題なんだよ。
嘘をつきまくってスレを荒らす行為は許されない。
なにか反論があるか?
>>461 あなたの頭のみを使ってください
受験会場に持ち込み可能なもののみ使いなさい
>>462 それはあなたの感想。
まるであなたがこのスレのルールを決めたかのようで、傲慢な人間性が表れていますね。
人間老いるとかくも汚くなるものですか。20の私に説教される恥を知りなさい。
>>465 年上でも人生終わってるジジイはただの加齢臭肉なんで
rは0<r<100の実数の定数とする。
方程式
x^100-2x^r+1=0
が持つ実数解の個数を求めよ。
>>467 私ならこうしますね
rは0<r<100の実数の定数とする。
方程式
x^100-2x^r+1=0
が持つ複素数解の個数が、重複を含めて101個以上となることはあるか。
>>464 感想ではなく客観的事実を述べている。
おまえの人間性が腐ってるというのは俺の感想だが、
少なくともお前が嘘つきだというのは客観的事実だ。
スレのルールはスレタイが語っている。それもわからんのは
ボケ爺さんだけだろう。しかし、自作爺さんが老いを語ると
は笑止千万だなw
>人間老いるとかくも汚くなるものですか。
まさにおまえのことだろ。年齢詐称、出典詐称、学歴詐称。
嘘ばかりつく薄汚い糞爺、それが自作爺さん、おまえだよ。
>>466 おい、加齢臭肉!
おまえの人生が終わってるからこんなところで日がな一日クソ問題を
出し続けてスレを荒らしてるんだろ。
たいがいにしろよ、クソジジイ
>>463 皮膚科の進級試験は教科書・ノート持ち込み可だった。
正しい診断ができるなら手段は問わない、という哲学の教授だった。
既に鬼籍に入られたが。
教養課程での物理の試験は電卓持ち込み可だった。
俺はTIのプログラム電卓に関数入力して試験に臨んだ。
教授は物珍しそうにそれはプログラム電卓か?と話しかけてきたが別に咎められることもなかった。
途中で充電が切れて手計算する羽目になってあせった。
>>471 乱数使ってシミュレーションして求めて下さい
0から1までで定義される一様分布に従う確率変数Xの逆数の期待値は?
>>472 加齢臭肉の朝は早い
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>469 このスレだってあなたが立てたんでしょう?
スレのルールについて全員の合意なんてあるんですか?
あなたの独り善がりじゃないんですか?
>>470 すいませんジジイはあなたなんてすよね…
私は与作なんて知らないんで、そんなネタが受けると思ってるあなたの感性ヤバいですよ
>>471 それ大学の話ですよね?
ここ高校数学のスレなんですけど
モーニング質問します
nを3以上の整数とする。
3辺の長さがn,n+1,n+2の三角形の面積が有理数となるnをすべて求めよ。
>>476 なんの反論にもなっていない。
おまえは独善にすらなってない。スレ違いだと知りつつ(複数の人間から
そう指摘され続けてるだろ?)確信犯的に悪行を重ねてる下劣な人間だよ。
>>477 年齢詐称、学歴詐称、出典詐称の加齢臭肉はお前のことだよ。
与作を知らないからって、爺でないことにはならん。
反論あるか?
さっさとカラオケで練習しとけ。 > ID:tljrnofJ
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>481 いや爺はあなたですよね?
与作って調べたら平成ですらないと分かりましたが、さらにその替歌(?)しようって発想が昭和確定じゃないですか
以下の命題の真偽を述べよ。
「任意の正整数pに対してある整数(n,k)で、等式n^2-p=3^kを成立させるものが存在する」
>>483 昭和生まれなら与作は知ってる人は知ってるだろ。大正生まれでも知らない人は知らない。
なんの反論にもなってない。
そもそも、おまえが大嘘つきの下劣な人間であるということと、爺であるかどうかは別問題。
爺だからダメだと言ってるわけではない。
>>483 おまえは加齢臭どころか腐臭が漂う腐肉だな。
性根が腐ってるんだよ。
さっさとカラオケで練習しとけ。 > ID:tljrnofJ
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>485 だから、あなたは爺ですよね?って(答えは分かってるけど)聞いてあげてるんですよ
与作www
>>486 あらあら人格否定ですか。
下劣な人間のすることです。
>>487 あなた自身が荒らしであることの自覚、あります?
(n+2)(n-2)=3^kは
自然数解をもたない
線形回帰分析で
回帰直線への距離で最小二乗法して算出した回帰直線の決定係数の算出の仕方を教えてください。
主成分回帰やダミング回帰で調べてもなかなか辿り着きません
>>496 すみません。大学レベル質問スレに気が付きませんでした。出ていきます。
>>489 なにをいまさら。
おまえの人格はクズだと2スレくらい前から言われ続けてるだろ。
実際、平気で嘘をつくやつの人格は否定されて当たり前だよ。
死ぬ死ぬ詐欺はどうなったんだ?
>>490 おまえは自分が荒らしであることを自覚してやってるから
腐臭漂う品性下劣なクズ野郎だと言われてるんだよ。
わかってんのか?
>>496 おまえにそんなことを指摘する資格があると思ってんのか?
嘘ばかりついてるクズ人間が言うことかよw
ちゃんちゃらおかしいわ。
さっさとカラオケで練習しとけ。 > ID:tljrnofJ
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
>>500 すいませんあなたが答える番なのですが…。
あなた自身が荒らしであるという自覚、あります?
この一点だけお答えください。よろしくお願いいたします。
本日の締めの質問です。
xy平面上の円x^2+y^2=3上の有理点を5つ求めよ。
すみません気になったので質問させて下さい
どこかの出題とかではありません
時速50kmを30m先まで照らすロービームで夜間走行する車が
30m先の時速0kmの歩行者とすれ違う時間は何秒ですか?
夜間走行しててふと思ったのですがすれ違う一瞬が何秒なのか知りたいです
>>505 空気の屈折率を1.000016とし、光は回折しないものとして計算した。
>>506>>507
有難うございます
2秒しかないのですね
夜間走行は気を付けるようにしますと共に歩行する際は反射するシールやたすきを身に付けるようにします
単に 時速50kmで30m進むのに掛かる秒数 じゃダメなの?
>>503 自覚はない。答えるまでもなく当たり前のこと。
おまえは荒らしと自覚しつつやってるから悪質なんだよ。
腐臭漂う品性下劣な最低最悪の人間だと自覚せよ。
>>510 自覚がない荒らしは最低の荒らしですよ
醜悪な昭和ジジイですね
お得意の昭和歌謡曲替え歌、なにか作ってくださいよ
n>1のとき 3^n-2^n=(3-2)Σ[k=1,n]3^(n-k)2^(k-1)>1だからダメ n=1のみ
>>512 自覚のある犯罪行為のほうが悪意性が高いので悪質なのは当たり前だよ、馬鹿。
俺はお前の荒らしを是正するためのレスをしてるだけで、おまえの荒らしより投稿数も少ない。
>>515 それ自己満足ですよね
・私のレス数を減らせていない
・そもそも荒らしかどうかをあなたの主観で決めている
はあ~(ため息)
昭和は頭悪すぎて困る
>>515 横からですけどあなたは数学と無関係な荒らし行為が目立ちますね。良問を厳選して質問するなどしてください。
>>516 どんどん質問してください。スレの数学力向上に役立っていますよ。
はあ~(ため息)
昭和は頭悪すぎて困る
>>515 一行問題を3つ出しますので、どれが良問か判定してください。
tan1°は有理数か。
∫[0,a] 1/(x^4+a^4) dx をaで表せ。
22/7とπの大小を比較せよ。
>>519 有理数である
a^2
昔は22/7=πだった
全部有名な良問ですね
>>494 これ、難しすぎるぞ。
n, k は自然数なんだよな?
n^2 = 4 + 3^k
n = √(4+3^k)
n を有理数と仮定すると
√(4+3^k) = a/b
b^2 (4+3^k) = a^2
?????????????????????
???? ここから不明 ????
??????????????????????
↑ ここが分からん。
よって矛盾が生じる。
したがって n は有理数ではなく、自然数ではない。
>>521 n+2=n-2+4だから
n+2とn-2が両方とも3で割れることはない
よって
もし(n+2)(n-2)=3^kならば
(n+2)(n-2)の素因子は3だけなので
n+2は3で割れてn-2=1でなければならない
するとn=3だからn+2=5となり不合理。
tan(x+y)=(tanx+tany)/(1-tanxtany)
よりtanxとtanyがどちらも有理数であればtan(x+y)も有理数
もしtan1が有理数ならtan(1+1)、tan(2+1)、・・・tan(30)も有理数で矛盾
>>522 あ、そっか、ありがとう。
「素数3」 に対して、
2つのうち、「両方が素でない」 っていうような
自然数の組みは存在しないんだな。
>>518 昭和が頭悪すぎるのなら、広中平祐も森重文も頭が悪いことになるなw
>>517,518
自演乙だなw
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
<<516
>・私のレス数を減らせていない
はあ?おまえが減らさない限り減らないだろ。俺がどうこうできるわけない。
頭悪すぎるな、自作爺さんw
百万回歌って反省しろ
自作は気が変♪
どあほー、どあほー♪
自演(こだま)がかえるよー♪
どあほー、どあほー♪
イナさんはレスをする♪
トンチンカン、トンチンカン♪
気立てのいいイナさん♪
トンチンカン、トンチンカン♪
自作ーじいさん、もう夜があける♪
自作ーじいさん、イナさんが呼んでいる♪
アーホー、アーホー♪
質問させてもらいますよ、頭のいい兄ちゃんならおせーてもらえると思いますんで。
二階同次微分方程式の解はe^(γt)をいきなり仮定してますが。
これって、どうやって思いついたんでしょうか?
霊感ですか?
>>528 線型代数、固有値問題。
要するに行列の標準形の問題に帰着する。次数下げ。どこの高校でも教わる基本的な内容だな。
微分方程式 y'=αy に帰着する。これの解が y=Ce^(αx) となるというのが質問の置き方の根拠。
これは一々「解く問題」ではなく、「微分したらα倍→指数関数」と覚えておいてよい問題。
>>529-530 兄ちゃんの頭が良い事はよくわかりました(読んでも俺がちんぷんかんぷんなんで)。
Fランク大しか出てねぇのでさっぱりですわー。池沼は引っ込んでろなんて冷たい
ことは言わないでね。
>>526 あのぉ…
私の「荒らしを是正する」とか言っておきながら、何もできてないじゃないですか
あなたの数学力も大したことないですし、昭和から長生きしてるのに恥ずかしくないんですか?
私を是正してみてくださいよwお待ちしております
微分方程式の話題はスレ違いなんでやめてください
微分方程式
y'=(e^y-1)/y
を解け。
>>533 >微分方程式の話題はスレ違いなんでやめてください
>>529の兄ちゃんは「どこの高校でも教えている基本的な内容」と書いてる
ので、基本的というからには重要だと思いますのでスレにぴったりなのでは?
>>529 お前今の高校の数学の課程知らないのかよwwww
てめー昭和どころか尋常小学校だろ
>>537 教えない現課程の怠慢なのであって、わたくしのせいではありません。
馬鹿が行く工業高校においてさえ、過渡現象を解くために微分方程式を
教えていたのですから、これから大学で学ぼうという優秀な生徒が行く
一般の高校なら教えてないとおかしいでしょ。
工業高校なんて高校じゃありませんな、作業員にしかなれないんで実質義務教育
でできる内容
と、工業高校卒、Fランク大卒のわたくしが申してるので間違いないです。
ちなみに、工業高校卒は口が悪くていやです。一緒に仕事したくありません。
まぁ無理やね
今の高校は受験予備校化してる
レベル高い高校ほどそう
つまり受験に絶対でない指導要領範囲外の事教えるはずがない
3年前の高2のときに高校数学全範囲終わったが微分方程式は習わなかった
京大で簡単なものを出すという以外、出す大学がなかったからね
京大受験者は変数分離形くらいはやってたと思うが
>>529 ゴミ野郎、お前の頭は昭和か大正で止まってんのか?
試しにこの簡単な微分方程式を解いてみろよ
y''=xy
俺の高校では今でも教えているけどな。とか言うと高校がばれるか(東京の国立(こくりつ)の高校)。
>>541 y''=xy⇔''-xy=0⇔(e^(-x²/2)y)'=0
e^(-x²/2)y=C
よってy=Ce^(x²/2)
これは高2でやったような導入問題だな。講師は東大の数学科院生だった(博士課程)。うちの高校の出身。
>>541 それ初等関数じゃないよ
解析関数だとして
y=Σanx^n
y''=Σ(n+2)(n+1)a<sub>n+2</sub>x^n
xy=Σa<sub>n-1</sub>x^n
a<sub>n</sub>=a<sub>n-3</sub>/n(n-1)
a<sub>2</sub>=0
a<sub>3m</sub>=a<sub>0</sub>/3m(3m-1)3(m-1)(3m-4)…3・2
a<sub>3m+1</sub>=a<sub>1</sub>/(3m+1)3m(3m-2)3(m-1)…4・3
a<sub>3m+2</sub>=0
y=a<sub>0</sub>(1+x^3/3・2+x^6/6・5・3・2+x^9/9・8・6・5・3・2+………)+a<sub>1</sub>x(1+x^3/4・3+x^6/7・6・4・3+x^9/10・9・7・6・4・3+……)
>>543 おほほほほほほ
ばーかゴミカス
エアリーの微分方程式も知らないのかゴミカス
ばか!あほ!くたばれwwwwww
>>532 そりゃ、是正勧告に応じなければなにも起きないよ。
おまえが荒らしたいと思えばどうしようもない。
しつこく是正勧告を続けるしかないのだよ。
低レベルの自作問題を入試問題と偽って出すようなろくでなし
はこのスレから出ていって欲しい。
自殺すると言ってみたり、学歴、年齢を偽ってみたり、あんた
どうかしてるわ。
>>545 本性を表してきたな、自作爺さんw
キチガイだったかw
(d^n/d(x^n))y=xy の解 y は どうなる?
>>543 y=Ce^(x²/2) のとき y'=xy y''=y+xy'=y+x^2y
変数 x に対する第一種エアリー関数は広義リーマン積分
{\displaystyle {\begin{aligned}\operatorname {Ai} (x)&
={\frac {1}{\pi }}\int _{0}^{\infty }\cos \left({\frac {t^{3}}{3}}+xt\right)~dt\\&\equiv {\frac {1}{\pi }}\lim _{b\to \infty }\int _{0}^{b}\cos \left({\frac {t^{3}}{3}}+xt\right)~dt\end{aligned}}}{\displaystyle {\begin{aligned}\operatorname {Ai} (x)&={\frac {1}{\pi }}\int _{0}^{\infty }\cos \left({\frac {t^{3}}{3}}+xt\right)~dt\\&\equiv {\frac {1}{\pi }}\lim _{b\to \infty }\int _{0}^{b}\cos \left({\frac {t^{3}}{3}}+xt\right)~dt\end{aligned}}}
として定義することができる。
これが収束することは、激しく振動するグラフの正の成分と負の成分とが
互いに打ち消し合う(これは部分積分で確認できる)ことによるものである。
関数 y = Ai(x) はエアリー方程式
{\displaystyle y''-xy=0}{\displaystyle y''-xy=0}
を満足する。この方程式は二つの線型独立な解を持つ。
スカラー倍の違いを除いて、Ai(x) は x → ∞ で y → 0 なる条件を満たす
唯一の解である。もう一つの解として第二種エアリー関数 Bi(x) を取るのが
標準的である。第二種エアリー関数は第一種エアリー関数 Ai(x) と同じ振幅を持ち
x → -∞ で位相が π/2 だけ異なる解
{\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }
\left[\exp \left(-{\frac {t^{3}}{3}}+xt\right)+\sin \left({\frac {t^{3}}{3}}+xt\right)\right]dt}{\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\left[\exp \left(-{\frac {t^{3}}{3}}+xt\right)+\sin \left({\frac {t^{3}}{3}}+xt\right)\right]dt}
として定義することができる。
ごめんよ教えてください
1年末に1万円、2年末に2万円3年末に3万円積み立てて第三年末に引き出す時の元利合計はいくら?
利子10%とする。
私に質問を止めてほしいというなら相応の文章を以て書き込みをしなさい。
【質問】
p,qを実数の定数とする。
xy平面上の直線y=p(x-1)+q(x-1)について、以下の問いに答えよ。
(1)s,tを実数とする。この直線は点(s,t)を通りうるか。
(2)この直線が放物線y=x^2に接するような(p,q)をすべて求めよ。
∫[0,2a] 1/(x^4+4a^4) dx を求めよ。
1/7は0.142857142857...と循環しますが、2/7,3/7,4/7,5/7,6/7がいずれもこの循環節をスライドした形になるのはなぜですか?
たとえば2/7=0.285714285714...です。
またこのような分数n/mは1/7以外にどのようなものがありますか?
前
>>421 >>554 (2)D=(p+q)^2-4(p+q)=0
p+q=0,4
q=-p,4-p
任意のpに対し(p,q)=(p,-p),(p,4-p)
>>553 1*1.1^2+2*1.1^1+3*1.1^0
0≦x<1とする
√(1-x^2)-1=-x^2/(√(1-x^2)+1)<-x^2/2 より 1/√(1-x^2)>1/(1-x^2/2)
f(x)=√(1-x^2)-(1-x^2/2-x^4/8) と置くと
f'(x)=-x/√(1-x^2)+x+x^3/2<-x/(1-x^2/2)+x+x^3/2
=x/(1-x^2/2){-1+(1+x^2/2)(1-x^2/2)}=-x^5/4/(1-x^2/2)<0 f(0)=0より
√(1-x^2)≦1-x^2/2-x^4/8 等号成立はx=0
∫[0,1/2]√(1-x^2)dx<∫[0,1/2](1-x^2/2-x^4/8)dx
=1/2-1/6/8-1/40/32=(1920-80-3)/3840=1837/3840
左辺=∫[0,π/6](cost)^2dt=∫[0,π/6](1+cos(2t))dt/2=π/12+√3/8だから
π/12+√3/8<1837/3840 π<1837/320-3√3/2
もしπ>22/7ならば 22/7<1837/320-3√3/2 √27<1837/160-44/7=5819/1120
27<33860761/1254400<27 ゆえに π<22/7
(C[2n,2j])^2 のj=0からnまでの和は
( C[2n,n]*(-1)^n + C[4n,2n] )/2
になるらしいんですが、この示す証明はのは難しいでしょうか。
>>560 翌年は
1*1.1^3+2*1.1^2+3*1.1^1
((1+x)^(2n)+(1-x)^(2n))(1+x)^(2n)
=(1+x)^(4n)+(1-x^2)^(2n)。
x^(2n)の係数。
>>556 9 , 99 , 999 , 9999 ,..., 10^(m-2)-1 等全てが m で割り切れず、
10^(m-1)-1 が m で割り切れる場合
7,17,19,23,29,47,49,59,61,97等
スタート地点が m-1 通りあり、周期が m-1 なら、見える景色は同じ。
出発点が違うだけの「スライドした形」と見えてしまう。
確率変数が関数なのに変数と命名されている理由がいまいちよく分からない。
そこを丁寧に説明してくれている教材がほとんどない。
図書館や書店でいろいろ探してみましたが。
a,bを0<a<bの実数とする。
xy平面上の2つの楕円の周および内部
D1:ax^2+by^2≦1
D2:bx^2+ay^2≦1
を考える。領域D1∩D2の面積をa,bで表せ。
二つの楕円の交点の一つは x=y=1/√(a+b)
D1をy方向に√(b/a)倍すると円D3 x^2+y^2=1/a になる
領域y>0、x<0<1/√(a+b) にある円D3の面積は
∫[0,1/√(a+b)]√(1/a-x^2)dx=1/a∫[0,√(a/(a+b))]√(1-(x√a)^2)d(x√a)
=1/a∫[0,arcsin(√(a/(a+b)))](cost)^2dt
=∫[0,arcsin(√(a/(a+b)))](1+cos(2t))dt/(2a)
=arcsin(√(a/(a+b)))/(2a)+sin(2arcsin(√(a/(a+b))))/(4a)
だからこの領域にあるD1の面積はこれを√(a/b)した
arcsin(√(a/(a+b)))/(2√(ab))+sin(2arcsin(√(a/(a+b))))/(4√(ab)) になる
ここから一辺が1/√(a+b)の正方形を取り除いた部分の面積をSとすれば
この正方形4つとSを8つ足した
4arcsin(√(a/(a+b)))/√(ab)+2sin(2arcsin(√(a/(a+b))))/√(ab)-4/(a+b)
が題意の面積
>>563 ありごとうございます。
左辺の対応がいまいちわからんけれ
もちっとていねいにおしえておくれんかなもし。
>>571 ありがとうございます
広島大の過去問に同様の出題があったので一般のa,bの場合はどうなるか興味がありました
逆三角関数が入ってくるということは高校範囲では出せないですね
また円を拡大縮小する方法が有効だということも教えていただいてありがとうございます
x=sint/√a y=cost/√b dx/dt=cost/√a
∫[0,1/√(a+b)]ydx=∫[0,arcsin(√(a/(a+b)))](cost)^2dt/√(ab) でよかった
nは正整数の定数とする。
0≦k≦nをみたす正整数kで、
a[n,k]=C[n,k]*C[n+k,n-k]
を最大にするようなものをnで表せ。
n+k≧nk としてよい
k=0のとき成り立ち、a[n,0]=C[n,0]^2=1
k=1のとき成り立ち、a[n,1]=C[n,1]C[n+1,n]=n(n+1)
k>1のとき n≦k/(k-1)<2 より n≦1 だから矛盾
k=1で最大
a,bは1<a<bの実数の定数とする。
f(x)=(1+x)(1+ax)(1+bx)
について、以下の問いに答えよ。
(1)f(x)は極大値と極小値を1つずつ持つことを示せ。
(2)(1)の極大値をとるxの値をα、極小値をとるxの値をβとする。またxy平面における2点A(α,f(α)),B(β,f(β))を通る直線をLとする。Lの方程式をa,bで表せ。
(3)Lと曲線y=f(x)とで囲まれる領域の面積をa,bで表せ。
前
>>579 (1)f(x)=ab(x+1)(x+1/a)(x+1/b)
-b<-a<-1<-1/a<-1/b<0<1/b<1/a<1<a<b
f(-1)=f(-1/a)=f(-1/b)=0よりグラフを描くとy=f(x)は-1<x<-1/aに極大値を持ち、-1/a<x<-1/bに極小値を持つとわかる。
(2)直線Lの方程式は、
y={ab(α^2+αβ+β^2)+(ab+a+b)(α+β)+1+a+b}(x+1/a)
解と係数の関係よりαとβを消去すると、
これだけの情報でa、b、c、dの座標を求めることは可能でしょうか?

>>581 いいえ,これだけでは一意に定まりません。
例えば内側の灰色部が長方形ならば,
追加で1点の座標が定まれば
・ 向かい合う辺同士のベクトルが等しい
・ 隣り合う辺の内積が0(直角)
等で立式できると思います。
酉間違えちゃった
追記で,内側の長方形の縦横比が定まっているパターンなどでも求まります。
>>521-524 先週の書き込みだけど
我ながら己がアホすぎてワロタw
よくこれで大学卒業できたな、すげぇや、おれ ( '‘ω‘)
>>584 そんなことはない
何を考えたかがわかるように書けるというのは
大学教育の最も大きな成果ではないか
aを実数の定数とする。
lim[x→0] (e^x-cosx)/(e^x-asinx-1)
を求めよ。
高校数学スレでasin(x)とかアホじゃないの?
解答ならともかく問題に書くって
C[n,k+1]=n!/(k+1)!/(n-k-1)!=n!/{(k+1)k!}/{(n-k)!/(n-k)}=(n-k)/(k+1)C[n,k]
C[n+k+1,n-k-1]=(n+k+1)!/(n-k-1)!/(2k+2)!
=(n+k+1)(n+k)!/{(n-k)!/(n-k)}/{(2k+2)(2k+1)(2k)!}
=(n+k+1)(n-k)/(2(k+1)(2k+1))C[n+k,n-k]
a[n,k+1]/a[n,k]=(n-k)/(k+1)*(n+k+1)(n-k)/(2(k+1)(2k+1))
=(n-k)^2(n+k+1)/{2(k+1)^2(2k+1)}
右辺の分子はn^kをtと置けばt^2(2n+1-t)だから0≦t≦nで増加するからkの減少関数
分母は増加関数、右辺の分子-分母をf(k)と置いてkを実数と見てf(k)=0を解けばいい
f(n/2)<0<f(n/3)だからこの範囲にf(k)=0の唯一の解があってそれをk=αと書けば
f([α]+1)<f(α)=0≦f([α])だから a[n,[α]+2]<a[n,[α]+1] a[n,[α]]≦a[n,[α]+1]
k=[α]+1で最大
x^3+Ax^2+Bx+C=0でx=t-A/3と置くと二次の係数が0のt^3-3at-b=0に直せる
これを (x+y)^3-3xy(x+y)-(x^3+y^3)=0 と見て bx^3=x^6+a^3だから
x^3=1/2{b±√(b^2-4a^3)} y^3=b-x^3=1/2{b-±√(b^2-4a^3)}
1の立方根の一つ-1/2-i√3/2をωと書くと x^3-a^3=(x-a)(x-ωa)(x-ω^2a) だから
t=x+y={1/2{b+√(b^2-4a^3)}}^(1/3)+{1/2{b-√(b^2-4a^3)}}^(1/3)
またはt=ω{1/2{b+√(b^2-4a^3)}}^(1/3)+ω^2{1/2{b-√(b^2-4a^3)}}^(1/3)
またはt=ω^2{1/2{b+√(b^2-4a^3)}}^(1/3)+ω{1/2{b-√(b^2-4a^3)}}^(1/3)
>>587 aは実数の定数と書きました
a*sinxでございます
>>586 なお高校数学のみで解けますのであえて誘導無しで質問しました
よろしくお願いいたします
s,t,u,v,wを0とxの間の数とする
e^x-1=e^x-e^0=xe^s cosx-1=cosx-cos0=-xsint sinx=sinx-sin0=xcosu
(e^x-cosx)/(e^x-asinx-1)=(e^x-1-(cosx-1))/(e^x-1-asinx)
=(xe^s-(-xsint))/(xe^v-axcosw)=(e^s+sint)/(e^v-acosw)→1/(1-a) (x→0)
間違えた
a≠1の場合は1/(1-a)、a=1のときは発散する
矢野健太郎の公式集と旺文社の公式集どちらがオヌヌメですか(´・ω・`)?
>>585 良いこと言うな、おまえ、見込み有るぞ ( '‘ω‘)
初歩的な質問ですみません、
√25の3乗根=5の3乗根ではないのですか?教科書には5の2/3乗=√25の3乗根として書かれていたのですが、なぜそうなるのか解りません。
>>596 25の3乗根が5^(2/3) の間違いだと思います。
念のため,ルートの1画目の上に小さく3が書いてある記号は全体で3乗根を表します。
それっぽいな。
>>596さんは 3√25 を √25の3乗根 だと思いこんでるのでは?
>>596みたいなのがほんとの質問なんだよなぁ。
>>590みたいな自作厨がスレを荒らしてるのは迷惑でしかない。死んで欲しい。
>>600 君が触るから嬉しがるのでは?
無視してればいいと思うよ
a とa^a が無理数で、(a^a)^aが有理数になるような例はありますか?
>>604 √2 などがその実例ですが,高校数学の範囲を超えます。
(一応, ゲルフォント=シュナイダーの定理 を使うと示せます)
>>582 ありがとうございます。
本当はグレーの長方形を2等分する線(右に傾いてる方の線)を引きたかったんですよ
その線は外の大きい四角形の頂点を結べば引けるけど、その引いた線とグレーの長方形の交点の座標がわかりませんよね?
長方形を線にするプログラムを考えていました。
与えられたら情報は図に記入してある座標だけです。
>>562 おかげで自信満々でテストに取り組めました!
ありがとうございました!
>>582 こういうことなのですが…

外の正方形を(0,0),(0,1),(1,1),(0,1)に変えて考える
a=c、b=d=1-a だから (x2,y2)=(a/2,a/2) (x1,y1)=((b+1)/2,(b+1)/2)
>>609 今回たまたま外の四角形が正方形みたいになったけど、どんなグレーの長方形でも必ずa=cになるのかな?
ちょっと作図してみます
>>609 
どうやっても正方形になるんですね
不思議だな
ありがとうございます
>>601 結局あほな自作問題しか出せない低能ぶりにビックリだわw
せめて質問にすりゃいいのに、ほんと馬鹿w
>>603 無視したさ。
だけど、自作厨の愚問に答えようとするか馬鹿がいるからいつまでも消えないんだよ。
>>613←この馬鹿は「○○さんは別」とか言って回答を許容していた笑
>>613 それって結局あなたが虚しい戦いをしているということですよね(笑)
>>613 他人の行動を変えようとしても無駄ってことだよ
ある日、午前中に雪が降り始めた。
雪はつねに一定のペースで降る。
除雪車が正午(AM12時)ぴったりに動き出し、1時間で2マイルの除雪を完了し、さらに1時間で1マイルの除雪を完了した。
雪はいつ降り始めた?
除雪ペースについて忖度できないアスペを殺すための問題ですね
降雪量がv(m/h)、積雪量x(m)である場合に除雪ベースがf(x)(mile/h)、正午の時点での降雪量をx₀(m)とする
正午からt(h)後の時点での降雪ペースは
f(x₀+vt)(mile/h)
条件は
∫[0,1] f(x₀+vt)dt = 2
∫[1,2] f(x₀+vt)dt = 1
除雪車が時間あたり一定の量を除雪すると仮定する
時点tでの雪の高さをyする 正午をt=0とし y=a(t+b) と置く
時点t=0からt=Tまでに除雪車が進んだ距離をxとする
時点tにおける除雪車の速度はその時点での雪の高さに反比例するので
dx/dt=Aa/yと置けるから x=A∫[0,T]dt/y=Alog((T+b)/b)
T=1のときx=2だから 1=Alog((1+1/b) e^(1/A)=1+1/b
T=2のときx=3だから 3=Alog(1+2/b) e^(3/A)=1+2/b
(1+1/b)^3=1+2/b k^3=2k+1 解の一つはk=-1だから(k+1)(k^2-k-1)
k=1+1/b=-1,(1±√5)/2 bは正だから適するのはk=(1+√5)/2のみ すなわちb=(1+√5)/2
正午の(1+√5)/2時間前
>T=1のときx=2だから 1=Alog((1+1/b) e^(1/A)=1+1/b
間違えた
T=1のときx=2だから 2=Alog((1+1/b) e^(2/A)=1+1/b
だった
T=2のときx=3だから 3=Alog(1+2/b) e^(3/A)=1+2/b
だから(1+1/b)^3=(1+2/b)^2 k^3=(2k-1)^2 k^3-4k^2+4k-1=0
とりあえずk=1は解だから(k+1)(k^2-5k+1)=0 k=-1,(5±√21)/2
b=1/(k-1)が正になるのはb=(√21-1)/10のみ 正午の(√21-1)/10時間前
>>569 数列はフィードバックループを行った再帰関数なんですか?
>>623 漸化式で表された数列はそうですね。
(元レスはもっと一般に,実数列は N→R の要素に過ぎないという意味だと思います)
3項間漸化式で表されるの増減について質問です
a,p,qは実数の定数とします。
a[0]=0
a[1]=a
a[n+2]=pa[n+1]+qa[n]
で表される数列{a[n]}の増減を、a,p,qの値により分類したいのですが、高校範囲で可能でしょうか。
分類というのは、例えば「単調増加」「○個の極小値を持つ」などを指します。
(a[n],a[n+1]) は二次曲線上を動く
楕円ならくるくる回る
放物線、双曲線ならどっかからスタートして一方に進む
>>614 イナさんは誰にでもトンチンカンな回答をするから例外なんだよ。
少なくとも彼には自作厨のような悪意はないし、コテハンでやるだけ誠意がある。
彼に比べれば、数学的能力は同じくらいでも自作厨はクズ。
>>615 違うよ。
>>587は別人だ。
>>617。
自作厨に少しでも良心があれば変えられたかもしれない。
自作厨がどういう愚劣感であるかを知らしめることに意味がある。
自作問題を「質問」と言って憚らない大馬鹿者に回答するのは
頭が足りない人だけだよね。
>>631 頭が足りないのはあなたもでは?
相手しないのが一番
5chごときで意地になって荒らしと成り果ててるあなたが滑稽でならない
lim[n→∞] {Σ[k=1,n-1] 1/C[n,k]}
を求めよ。
>>629 ありがとうございます。これからも良質な質問を続けて行きますね。
2次方程式
x^2-kx+1=0
x^2+2kx-1=0
がともに相異なる2つの実数解を持つとする。それらの中で最大のものをα、最小のものをβとおくとき、α-β=2√5となる実数の定数kの値をすべて求めよ。
>>637 問題としては簡単だけどめんどくさすぎ
それぞれの解の大きい方を表すkの関数2つのmax
小さい方を表すkの関数2つのminを考えて
その差が2√5の場所をチェックするだけ
やる気が起こらん
2r(k^2+1)<=2r5.
k^2<=4.
4<k^2.
4<4.
おはようございます
朝の質問です
nを非負整数とする。
8n^2+1が2n+1で割り切れるようなnをすべて決定せよ。
1/4メートル=25センチですが両辺のルートをとると
1/2メートル=5センチになり成り立たなくなってしまいます
なんで
xメートルは100xセンチが定義
これを両辺でルートを取れば√xメートルは√(100x)=10√xセンチとなり定義が壊れる
8n^2+1=(4n-2)(2n+1)+3 だから (8n^2+1)/(2n+1)=4n-2+3/(2n+1)
右辺の最後の項 3/(2n+1) はn=0,1のとき整数だが2以上だと非整数
8だといくら何でも簡単すぎるから2や奇数にすればいいのに
8を2に変えた場合 2n^2+1=(n-1/2)(2n+1)+3/2 だから
(2n^2+1)/(2n+1)=n-1/2+3/(4n+2)
n=0,1のとき左辺は1 nが2以上のとき n-1/2<右辺≦n-1/2+3/(4*2+2)=n-1/5
整数にならないので不適
Σ[k=1,n-1]1/C[n,k]<1/C[n,1]+(n-3)/C[n,2]+1/C[n,n-1]
=1/n+(n-3)2/(n(n-1))+1/n→0(n→∞)
>>xメートルは100xセンチが定義
>>これを両辺でルートを取れば√xメートルは√(100x)=10√xセンチとなり定義が壊れる
√は両辺でそれぞれメートルとセンチまでかかっている
i.imgur.com/F7MdHq9.jpg
確率の問題です。
↑の(3)を満たしているかどうかのチェックって要りますか?
そもそも X の期待値が 0 でも 100 でもないので、 0 < a < 100 は明らかです。
「X の期待値が 16/5, 分散が 64/25 であるとき、袋の中の赤玉の個数 a および回数 n を求めよ。」
と書いてありますが、これを満たす、 a および n が存在するということは前提になっているのでは
ないでしょうか?
訂正します:
i.imgur.com/F7MdHq9.jpg
確率の問題です。
↑の(3)を満たしているかどうかのチェックって要りますか?
そもそも X の期待値が 0 でも n でもないので、 0 < a < 100 は明らかです。
「X の期待値が 16/5, 分散が 64/25 であるとき、袋の中の赤玉の個数 a および回数 n を求めよ。」
と書いてありますが、これを満たす、 a および n が存在するということは前提になっているのでは
ないでしょうか?
例えば、何かの個数を求める問題で、得られた答えが 0 以上の整数であるかどうかいちいち
チェックして、解答に「答えは 0 以上の整数である。」とか書く人などいませんよね?
0 < a/100 <1 であることをチェックしていますが、
0 ≦ a/100 ≦ 1 であることをチェックしていないのはなぜですか?
0 または 1 だと何か不都合はあるのですか?
この問題は有名な?チャート式という参考書に載っている問題と解答です。
サッカーでボールが出たか入っていたかが話題になってるけど
角度によって球と線が最大どれだけ離れているように見えるかってわかりますか?
S: x^2+y^2+z^2=1
L: 2平面x=1とz=-1の交点
SとLを平面Pに射影するときに距離が最大となるPは?
おれなら 分散/期待値={np(1-p)}/{np}=1-p=1-a/100=4/5 から行くわ
>>664 で、結局、(3)のチェックは不要ですか?必要ですか?
チャート式という数学の参考書は、「チャート研究所編著」となっています。
素人が書いているからでしょうか、おかしなところが多くあるように思います。
前
>>646 >>662 球x^2+y^2+z^2=1の射影は半径1の円だから、
平面x=1とz=-1の交線(1,0,-1)+t(0,1,0)との距離の最大値は√2-1
∴平面Pはx+z=a(aは任意)
>>665 おれなら書かないが必要説に興味があるので他の人に聞いてくれ
あとa,b,cは非負でa+b+c=100なんだから直に0≦a≦100が出るので③の出し方だるい
自作問題警察ジジイがついに何も言わなくなったな
よほど堪えたと見えるw
>>657 >i.imgur.com/F7MdHq9.jpg
この問題さ
「n回繰り返す」という試行を「1回だけ」と解釈できる余地が無いかね
その場合Xの実現値に付いての情報だけになって答えが存在しないことにならないかな
余地も何も期待値と分散は「1回だけ」で決まるものだが
>>672 期待値と言わず平均値と言うならしっくりくるけど
xは0<x<π/3を満たす実数とする。
3辺の長さがsinx,sin2x,sin3xである三角形が存在するとき、sinxの取りうる値の範囲を求めよ。
f(x)を整数係数の1次関数とする(xの1次の係数は0でない)。
g(x)=1+{f(x)}^2,h(x)=g(x)-{g'(x)}^2とするとき、以下の問いに答えよ。
(1)f(x)=ax+bに対してh(x)を求めよ。
(2)h(x)が定数になることがあるならば、そのような整数の組(m,n)が満たすべき必要十分条件を求めよ。ここでmはf(x)の0でない1次の係数、nは定数項である。
>>672 「期待値」が?
>>674の言うように「平均値」と解釈できる余地があるから君はそう解釈したのじゃないかね?
けれどそれなら1回限りだから何も決まらないよ
>>673 混乱させるため
嫌がらせのようなものだけど
ちゃんとそれを見抜かせるのも目的
あるいは
もっと展開する設問だったのを
一部だけ切り出したかも
書いたのが改題できない無能って話なら救いようがないけど、
単なる嫌がらせ目的の3色ならまだマシか
じぶんも
無理矢理な解釈ができないとも限らないのではと思っただけだし
くだらない問題で喧嘩しないで
この傑作
>>676に答えてください
>>681 二項分布の期待値はnp、n=1のときはpです
>>676 g(x)=1+(ax+b)^2=a^2*x^2+2abx+b^2+1
{g'(x)}^2=4{(a^2)x+ab}^2
=4{(a^4)x^2+2(a^3)bx+(ab)^2}
g(x)-{g'(x)}^2
=(a^2){1-4(a^2)}x^2+2ab(1-a^2)x+1-(ab)^2
よって
a=0かつbは任意の実数
または
a=±1/2かつb=0
場合分けが美しい…
C[n,k]^2=c_kとおいてn次の整式 f(x)=Σ(c_k)*x^k (k=0からnの和)とします。
0<r<1として、f(r)/f(1)→0 (n→∞) はいえますか。
>>686 a,bの値が美しすぎます
狙って質問したわけではありません
>>657 改題
袋の中に100個玉が入っていてK個がアタリである。
一度にn個を取り出してアタリの数をXとする。
Xの期待値が5.5、分散が3.25であるとき
nとKの値を求めよ。
3色にして嫌がらするのが主目的の問題なんだから、改題したら全然意味ないじゃん
職種の云えない医療従事者=尿瓶おまる洗浄オムツ交換係を発見!
医師限定掲示板にはアクセスできず、5chアラシ専従。
>>693 荒らしはアンタだよ
m3じゃ相手にされず結局ここに舞い戻ってきた尿瓶ジジイw
哀れだねw
>>694 m3の医師限定掲示板に書けないのが尿瓶おまる洗浄オムツ交換係。
ゾコーバのデータを用いて日本人と韓越人に効果の差があるかを投稿したら賛同のレスがついたな。
異論があればm3 掲示板に書いてみたら?
m3 にアクセスしていたらポイントが貯まっていたのでアマゾンギフトカードに交換した。
>>696 Amazonギフトの一つ覚えで草
賛同のレスなんてどこにあんだよ?反対の嵐じゃねーかw
あっちでは表立ってバカにされなくていいねw
アマギフがステイタスだと思ってるおじさんがいますね
>>700 いや、尿瓶おまる洗浄オムツ交換係だと掲示板にアクセスできないからねぇ。
>>691 理論値の一つをシミュレーションして検算。

> summary(X); var(X)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000 4.000 5.000 5.502 7.000 14.000
[1] 3.249081
期待値5.5 分散3.25に近似しているので合っているんだろう。
>>701 こいつ医者のフリしてm3掲示板で喚いてるだけ
先生方からは総スルーなのを医師板のスレで晒されて発狂中w
>>703=尿瓶ジジイのm3掲示板でのご活躍を一部披露
No.664 2022年11月19日
投稿者:R-user
専門医なのに盲目的気管挿管やったことないの?
俺は開口困難例で盲目的経鼻挿管した経験がある。
食道に入るか気管に入るかの賭けだけどやらなきゃ気道確保の可能性を放棄することになる。
気管内投与できなきゃ、ボスミン心注も当然選択肢に入れる。
困難そうだからやらないじゃ、救命の可能性が0になる。
期待権の侵害で敗訴すると思う。
↑
ちなみに賛成0 反対16 www
この書き込みについての一医師のコメント
No.695
投稿者:miz-oka
気管内挿管もできないような医師がワクチン接種バイトするとはねぇ・・・
日本全体のワクチン接種の現場が判っているんかな??
それが出来る医師しかワクチン接種できなかったら、対応は全然できないよ。
僕は老齢で今は老人施設で結構まとまった数の接種業務を引き受けているけど、そもそも気管挿管の準備などありません。ボスミン注射などは一応準備しているけどね。
しかし、他の注射や点滴でも質的には同様のリスクがあるけど、普通の医療機関の医師が全部挿管の素養がないといけないはずがない。
自分が気管挿管が出来るからと言って偉そうにいい加減なことを言わない方がよいと僕は思うんだけど。(以下略
ちなみに賛成6 反対1
反対してるのはR-userこと尿瓶ジジイだけですwww
>>705 コピペじゃん、アンタがアクセスできたわけじゃなし。
>>705 コピペじゃん、アンタがアクセスできたわけじゃなし。
最近はゾコーバのスレに統計解析を書いてんだが
アクセスできんからわからんだろ。
m3 医師限定掲示板には尿瓶おまる洗浄オムツ交換係はアクセスできんからね。
それと掲示板の情報は外部に公開しませんをクリックしてアクセスしているはずなんだがね。
>>704 尿瓶おまる洗浄オムツ交換係はm3のクイズとかやらんの?
ポイントが貯まるぞ。

最近の国試は簡単な問題が多いな。まあ、簡単な問題に高正解率を要求しているようである。
尿瓶おまる洗浄オムツ交換係じゃアクセスする権利すらないんじゃね。
4連投もして発狂w
ここまで言われてなお書き込むなんてどれだけ図々しいんだ尿瓶ジジイはw
>>708 じゃあコピペじゃない尿瓶ジジイの書き込みも晒してやろうw
No.694 2022年11月20日
投稿者:R-user
辻褄のあう病状説明なら、クモ膜下出血によるneurogenic pulmonary edemaでも説明できそう。
まあ、AIやったらしいからSAHならその報道があっただろうから、その可能性はなさそう。
賛成 0
反対 3 ww
>>706 自分の投稿には賛成・反対をクリックできないのを知らないとはm3にアクセスできないからだろ。
695の投稿には、挿管できないことを偉そうに書くな、と俺と同意見のレスがついているよ。
713番の投稿をみてみ!ああ、見られないか。
尿瓶おまる洗浄オムツ交換係じゃ、医師限定掲示板にアクセスできんのだろ?
m3では業界ネタの議論ができて勉強になる。
最近の閲覧人数3位の「ピットフォールに落ちました」は明日は我が身でと身が引き締まるレスが多い。
>>713 晒された途端逃走したスレから急に舞い戻ってきて草
容赦なく反対押されてますw
No.714 11分前
投稿者:R-user
当院でも当直バイト医には、挿管・ナート必須という縛りをかけている。
先日、搬送されたCPAがコロナであるのが判明してCPRをしたバイト医は気の毒だったなぁ。自発呼吸ないから咳き込むことはなかっただろうけど、胸骨圧迫でウイルスが空気中を拡散したんじゃなかろうか。
賛成 0
反対 1
https://sp.m3.com/community/threads/437229?p=0 実数s,tは
0<s≦t≦1
0<s+t≦1
の範囲を動く。
(1)s,t,s+t,s^2+t^2を小さい順に並べよ。
(2)st(s+t)/(s^2+t^2)の最大値が存在するならば求めよ。
7^(1/3)と9^(1/3)のどちらが2に近いか。
前
>>667 >>716 y=x^(1/3)
y^3=x
第1象限においてグラフは上に凸だから、
9^(1/3)のほうが2に近い。
∴
>>712 神経原性肺水腫という
意見は俺以外にもあったぞ。
そういう臨床経験がないとか、気管チューブ挿管もできないのが反対しているだけ。
尿瓶おまる洗浄オムツ交換係は気管挿管できんのじゃね?
m3掲示板は尿瓶おまる洗浄オムツ交換係がアラシにこないので業界ネタの議論ができる。
>>714 反対しているのは気管挿管できない無能医だろ。
713番みてみろ。
基本的な救命措置ができない医師を断罪しているよ。
んで、尿瓶おまる洗浄オムツ交換係は気管挿管したことないだろう?
>>718 そこで相手にされないからこっちきてるんやろ
あ~あ、やっぱりこっち戻ってくるのか
そりや相手にされないわな
f(x)=x(x+k)(x+1)
とする。ただしkは0<k<1の実数である。
(1)f(x)は0<x<kの範囲でただ1つの極値をとることを示せ。
(2)(1)の極値をa[k]とする。極限
lim[k→0] a[k]
を求めよ。
f(x)はx=-1,x=-k,x=0を根に持つ三次式だから
-1<x<-kに極大が一つと-k<x<0に極小が一つあるがx>0には極値はない
>>719 気管内挿管とか言ってた脳内医者、気管挿管って言葉は覚えたか?w
じゃあ反対16も全員無能医なのか?w
>>723 そうだろう。
713で挿管できる医師が、挿管できない医師を断罪しているからね。
吐物や喀痰での窒息患者を救命できないような医師は当直には不要。
tを0<t<1の実数の定数とする。
f(x)=x(x-t)(x-1)
について、以下の問に答えよ。
(1)f(x)は0<x<tおよびt<x<1の範囲に極値を持つことを示せ。
(2)(1)の極値のうち、0<x<tに存在するものをα、t<x<1に存在するものをβとする。極限
lim[t→+0] α
lim[t→1-0] β
を求めよ。
前
>>717 >>726(1)
f(0)=f(t)=f(1)=0
x→-∞のときf(x)→-∞
0<x<tのときf(x)>0で上に凸。
t<x<1のときf(x)<0で下に凸。
x→+∞のときf(x)→+∞
∴y=f(x)のグラフの形よりf(x)は0<x<tおよびt<x<1の範囲に極値を持つ。
f'(x)=3x^2-(t+1)x+t=0
球の表面積を積分すると球の体積になる
4πr^2を積分して4/3πr^3となる
これはなぜか?文系では数学ができる部類の親父が不思議がってるんですが
誰か説明できますか?
医師がうらやましければ再受験でもすればいいのに。
新潟大学には看護助手から医師になった人物がいたぞ。
臨床医学は確率事象を扱うからこういう計算ができた方がいいね。
自分でできなければできる人に依頼すればいいけど
まわりが裏口シリツ医だと依頼できる人物がいなそうだなwww
袋の中に100個玉が入っていて、そのうち何個かがアタリである。
一度に100個の中から無作為に10個を取り出してアタリの個数を記録する。
記録したら10個の玉を戻して、再び無作為に10個取り出してアタリの個数を記録する。
これを50回繰り返ししたところ
以下の結果であった。
アタリの個数 0 1 2 3 4 5
その 頻 度 5 5 18 14 7 1
100個の中に含まれるアタリの個数として最も可能性が高いのは何個か?
>>730 お前には統計学も確率論も生涯理解できる日はやってこないよ
そんな知能はない
パソコンの前でキーボード叩いて喜んでるチンパンジー
a+(1/a)=-1 の時
(a-1)^12 の値を求めよ。
>>725 バカじゃねぇの?
賛成0で反対16って脳内医者って言われてるも同然だろマヌケ
>>738 だから問題になってないんだよバーカ
コレが問題になってない事が理解できないのがお前がチンパンジーである理由だよ
お前がキーボード叩いて出てきた数字の意味がわかってないからそんなアホ文章になるんだよ
ハッタリだと思うならそのアホ文章あちこちに貼りまくって永遠に恥晒せ
>>738 問題文もまともにつくれないどころか日本語も使えない脳内医者はお引き取りを
>>738 乱数使ってシミュレーションして求めて下さい
0から1までで定義される一様分布に従う確率変数Xの逆数の期待値は?
>>730 やり方は簡単なのに計算量が洒落にならん問題って一番くだらないよ
5chでゴミ扱いされるのがたまらなく快感みたいだね
>>738=尿瓶ジジイは
f(x)=x(x-t)(x-1)はtを0に近づけるとfはx^2(x-1)に近づくので極大は重根(0,0)に近づく
tを1に近づけるとfはx(x-1)^2に近づくので極小は重根(1,0)に近づく
>>728 表面積に厚みを掛けて足し合わせたものが体積だから
半径rの球の体積をV(r)、表面積をS(r)と置くと、V(r)=∫[0,r]S(t)dt
V(r+h)-V(r) はhS(r)より大きくhS(r+h)より小さいから
hS(r)<V(r+h)-V(r)<hS(r+h) と書けるので S(r)=V'(r)
a^2+a+1=0 a=-1/2±i√3/2
a-1=-3/2±i√3/2=√3{-√3/2±i/2}=√3e^(±i(5/6)π) (a-1)^12=3^6
>>728 「同じ速度で少しずつ敷き詰めていけばそうなる」
っていうのは具体例で考えたら分かるんでないの。
長さ 10cm の そうめん を1本ずつ同じ速度で
真横へ並べて敷き詰めればどうなるか。
最後には長方形 が得られる。(積分で線から平面へ)
おなじく、レタスの皮が剥がれたものを想像してもらいたい。
これを逆再生して、皮を1枚ずつ同じ速度で重ねていけば
最後には 質量のあるレタス1個 が得られる。
(積分で 曲面から球体へ)
>>747 この考え方で行くと
問い.1 ピザ (πr^2) をサイズを小刻みにかえて
同じ速度で敷き詰めていくとどうなるだろうか?
球体が得られる?
というのはひっかけで実際は三角錐が得られる。
なぜなら、同じ速度で敷き詰めていくと、球じゃなく三角錐(コーン状の物体)になるから。
サイズの変え方による
ピザの厚みをr/n、k枚目に重ねるピザの半径をr√(1-k^2/n^2)、とした場合、
k=1からk=nまで重ねれば半球に少し小さいピザ階段ができて、その体積は
Σ[k=1,n]πr^2{1-k^2/n^2}(r/n)=πr^3{1-n(n+1)(2n+1)/6/n^3}<πr^3(1-1/3)
k=0からk=n-1まで重ねれば半球に少し大きいピザ階段ができて、その体積は
Σ[k=0,n-1]πr^2{1-k^2/n^2}(r/n)=πr^3{1-(n-1)n(2n-1)/6/n^3}>πr^3(1-1/3)
>>728 円周の長さを積分したら円の面積になるようなものよ
>>689 Aut(R)、環の自己同型
Ker(φ)、φ(a)=0、a∈R、
環準同型φの核(Kernel)
0にうつるR₁の部分集合全体
φが単射⇔Ker(0)={0}
R₁/Ker(φ)、Image(φ)
>>689 環準同型φ:R₁→R₂に対して
環同型φ':R₁/Ker(φ)→Image(φ)
a'=a+Ker(φ)であることに注意する。φ'はwell-definedである。
φ:R₁→Image(φ)、
ψ:R₁→R₁/Ker(φ)、
φ':R₁/Kerφ→Imageφ
ψ:a→a'、φ:a→b、φ':a'→b'
b=b'
同型:R₁/Ker≅Imageということ
>>688 φが単射のときはR₁/Ker(φ)=R₁
φ:R→R/IのときKer=I、Image=R/I
φ'=id(R/I)は恒等写像。
環準同型φ:R[T]→R、
φ(f(T))=f(α)すなわち代入。
Kerφ=T-αよりR[T]/(T-α)≅R
>>750
その教え方だと
「おい、円の面積を積分しても球にならないぞ!」
ってクレームが入るぞ。 原点中心、半径rの球をz=tで切ったときの断面はx^2+y^2=r^2-t^2
面積はπ(r^2-t^2) これをz=0からz=tまで積分するとπ(tr^2-t^3/3)
>>688 R[T]/(T²+1)≅C
φ(f(T))=(f(1), f(-1))∈R×R
R[T]/(T²-1)≅R×R
Ker=5Z、2+i
Z/5Z≅Z/(2+i)
教えてください
統計力学は古典力学の範囲内ですか?
>>757 R[T]/(T²+aT+b)が整域
⇔D=a²-4b<0
Ker=T²+aT+b
D<0のとき、整域である
D=0のとき、整域ではない
D>0のとき、整域ではない
>>757 古典的にも量子的にも扱うことができます
ありがとうございます
統計力学は古典力学的にも量子力学的にも取り扱えるんですね
nは3以上の整数とする。
1,2,...,nのn個の整数から異なる2つを無作為に選び、それらの和をとる。その和がxとなる確率をp(x)とする。
3≦k≦2n-1である整数kについて、p(k)をkで表せ。
>>757 a∈Ker
⇔a≡0 modI₁かつa≡0 modI₂
⇔a∈I₁∩I₂
φが全射のとき
∃c₁∈R、φ(c₁)=(I₁, IR+I₂)
I₁=0+I₁∈R/I₁
c₁∈I₁かつc₁≡IR mod I₂
c₂=IR-c₁とおくと
c₂≡IR-c₁≡IR-IR≡0 modI₂より
c₂∈I₂
よってIR=c₁+c₂∈I₁+I₂
これはイデアルであるから
I₁+I₂=R
>>764 nは3以上の整数とする。
1,2,...,nのn個の整数から異なる2つを無作為に選び、それらの和をとる。その和がxとなる確率をp(x)とする。
3≦k≦2n-1である整数kについて、p(k)をkで表せ。
>>742 計算機で数秒で計算終了したが
んで答は?
>>766 765も数秒で終わらせてください
もちろん数値計算に逃げないでください
>>766 実測値から推測される超幾何分布のパラメータを求める問題。
最小二乗で計算するかAIC最小で計算するかで微妙に答が違った。
>>767 臨床医は数字がだせればそれでいいのよ。
数値積分や乱数発生で近似値が出せればそれで良し。
ゾコーバの有効推定もp=0.0407でいいらしい。
このレベルのエビデンスではPL配合顆粒に負けるから使う気はしない。
>>743 んで、答はだせたの?
信頼区間がどの手法で計算するかで異なるように
この答も唯一解があるわけでもないが、どの手法でも大差のない答になると思う。
実数pに対し、[p]はpを超えない最大の整数を表す。
aを実数の定数、nを整数の定数とするとき、等式
[ax]+[nax]=1
を満たす実数xをa,nで表せ。
>>766 計算機で数秒も掛かるような莫大な計算を要求するのは非常識です。
>>769 >臨床医は数字がだせればそれでいいのよ。
>数値積分や乱数発生で近似値が出せればそれで良し。
数字すら出せずに
>>741から逃げてるのが貴方です。
[x]≦x<[x]+1 x-1<[x]≦x
ax-1<[ax]≦ax nax-1<[nax]≦nax
(n+1)ax-2<[ax]+[nax]≦(n+1)ax
(n+1)ax-2<1≦(n+1)ax
1≦(n+1)ax<3 1/(n+1)/a≦x<3/(n+1)/a
>>745,747,750
完全には理解できませんが何となくはわかりました
積分は線から面が得られ、平面から立体が得られるんですね
お答えどうもありがとうございました
>>770 アンタに問題出せる知能なんかないだろ
ただの脳内医者
>>730 アタリ玉の数nを変化させてAICが最小になるようなnを求めればいいので
グラフにすると

n=28のときがAICが最小(残差平方和計算しても当然n=28で最小)
理論値と実測値をグラフにすると

おまけ、Rのコード
k=10
mn=100
X=rep(1:6,c(2,6,7,3,1,1))
n=length(X)
p=NULL
for(i in 0:k) p=c(p,mean(X==i))
aic=\(m) n*(log(2*pi*sum((p-dhyper(0:k,m,mn-m,k))^2)/n)+1)+2*(1+1)
x=0:100
y=sapply(x,aic)
plot(x,y,bty='l',pch=16,xlab='n',ylab='AIC')
x[which.min(y)]
計算量が洒落にならんって、手計算すんのかなぁ。
>>775 医者がうらやましければ再受験すればいいのに
俺の同期は2割くらいは再受験組だったぞ。
殆どが東大か京大卒だった、当時は阪大医学部には学士入学制度があったから阪大卒はいなかったな。
ソフトに計算させた結果を張り付けることの何が面白いのか全く分からん
>>772 0に近い値で除算することになるから、答が定まらんのじゃないの?
正規分布の逆数の分布とかも同じ。
>>779 >臨床医は数字がだせればそれでいいのよ。
>数値積分や乱数発生で近似値が出せればそれで良し。
と述べたのは貴方ですよ
乱数発生で近似値が出せないのは脳内医者なんですかね?
>>770 問題にすらなってないチンパンジーの鳴き声に何答えるんだよタコ
>>759 それも一理あるが厳しすぎる。
質問者の頭の程度に合わせた教え方をしてこそ教育だろう。
例え話に出した敷き詰めていくピザの半径の変化量、
これが一定の速度であるという事の
意味をを理解していない人もいるわけで…。
ち、ちなみに謙虚な神戸大卒 TOEIC700です…( ; ‘ω‘) ハァハァ
S^0は2点これをrで積分してD^1の長さ2r
S^1は円周2πrこれをrで積分してD^2の面積πr^2
S^2は球面4πr^2これをrで積分してD^3の体積4πr^3/3
n乗根を求めよということと、正の根を一つ求めることの違いは理解しています。
正の実数aについて、その正のn乗根(nは正の整数)は、n^√(a)と表されるそうですが、
n^√(a)は、必ず正の数のみを表すことが保証されているのでしょうか。
(負の根は、常に、-n^√(a)で表されるのでしょうか。)
根号がついて、参考書や教科書はこのあたりについて暗黙の了解にされているように思います。
>>778 問題になってないという椰子がいたので解答例を出しただけ。
>>780 一様分布乱数を書いたら求めてやってもいいぞ。
回答例とか言ってる時点で一義的な解がないのは明らかで反論になってないね
>>788 甘ったれるのもいい加減にして下さい
自分で言ったことですよね
>臨床医は数字がだせればそれでいいのよ。
>数値積分や乱数発生で近似値が出せればそれで良し。
乱数発生で近似値が出せないのは脳内医者ということでいいですね
前
>>727 >>730小中学校板に倣って、
10×5/50=1
20×5/50=2
30×18/50=10.8
40×14/50=11.2
50×7/50=7
60×1/50=1.2
1+2+10.8+11.2+7+1.2=33.2(個)
∴期待値は33個
nは正整数とする。
1+2+...+2^nの1の位の数字をa[n]とする。
a[n]を求めよ。
以下の極限は収束することを示し、その極限値に最も近い整数を求めよ。
lim[n→∞] {∫[0,n] (1+x^2)/√(1+x^4) dx - n}
【このスレで質問大会を開催します】
高校生の数覚を鍛えるべく、このスレで質問大会を開催します。
>>792 2≡2(mod10)
2^2≡4(mod10)
2^3≡8(mod10)
2^4≡6(mod10)
2^5≡2(mod10)より
1の位は2,4,8,6で循環してく、
n=4kの時k≧0 an=20k
n=4k-1の時k≧1 an=20(k-1)+14=20k-6
n=4k-2の時k≧1 an=20(k-1)+6=20k-14
n=4k-3の時k≧1 an=20(k-1)+2=20k-18
でどう?
>>785 について、
正の実数aについて、その正のn乗根(nは正の整数)n^√(a)は、常にn^√(a)>0ということで良いでしょうか。
>>777 脳内医者の誰が羨ましいんだって?
アンタはもうジジイだから受験してる間にお陀仏だねw
>>784 とりあえず親父に読ませてみたいと思います
どうもありがとうございます
1+x^2-x^4<(1+x^2)/√(1+x^4)<1+x^2
17/15<∫[0,1](1+x^2)/√(1+x^4)dx<4/3
1+x^-2-x^-4<(1+x^2)/√(1+x^4)<1+x^-2
n-1/n-1/3+1/(3n^3)<∫[1,n](1+x^2)/√(1+x^4)dx<n-1/n
n-1/n+1/(3n^3)+12/15<∫[0,n](1+x^2)/√(1+x^4)dx<n-1/n+4/3
4/5<lim[n→∞] {∫[0,n] (1+x^2)/√(1+x^4) dx - n}<4/3 最も近い整数は1
>>794 2ch数学五輪ピックは
本日を以って終了いたしましたZOY ( '‘ω‘)
質問させていただきます。
nが整数でn^2が3の倍数ならnも3の倍数は真という事を使って√3が無理数だと証明する問題についてなのですが、良く√3=a/b(abが互いに素な既約分数)と置き、α^2=3b^2を経由させて、命題からαを3の倍数と出し、次にα=3cと置いて以下略というパターンを見ます。
然しこれはαが3の倍数と分かった後にα^2=3b^2 からb^2=a^2/3という方面に持っていっても上手く証明できますでしょうか。
できなくないけど目クソ鼻クソの差しかない
結局高校までの整数の性質の単元は「当たり前でない事を当たり前のフリする」しか単元として成立しない
じゃあどう誤魔化すのがいいのかだけど、やはりそれは「極力ごまかさない」につきる
ごまかさないで普通にやるなら
・ユークリッドの互除法
(a,b) = (a-b,b)
・べズーの定理(の一部)
(a,b)=1 → ax+by = 1は整数解をもつ
・規約元→素元
p が1と自分自身しか約数を持たない、abがpの倍数→aかbのいずれかはpの倍数
の流れが一般的だろうし、その意味でなら
「xyが3の倍数→xまたはyが3の倍数、特にx²が3の倍数ならxは3の倍数」
はかなり手短ないい証明
整数の性質の証明の単元の証明でよく「こんないい証明見つけた」みたいなの見かけるけど、大概よくよく精査すると余計な回り道してるだけのやつが多い
>>791 詐欺に騙されました
イナさんは詐欺に騙されたことありますか?
>>803 ご親切に回答くださりありがとうございます。
自分には少し内容が難しかったので、ゆっくりとお答えくださった内容を調べさせていただきます。
>>720 んで気管挿管したことあんの?
713番読んだ?挿管できないのを自慢するなと批判されていたよ。
m3掲示板で低血糖が話大になっていたので平田病に言及しておいた。
>>720 んで気管挿管したことあんの?
713番読んだ?挿管できないのを自慢するなと批判されていたよ。
m3掲示板で低血糖が話大になっていたので平田病に言及しておいた。
>>720 自作問題の投稿も構わんと思った(>2)から俺がスレ建てしたよ。
答に自信がもてないときとか別法で解のレスがくると安心できる。プログラムを使って総当たりとかシミュレーションである程度確信がもてるけど。
>>791 100個中アタリが33個のときと25個のときの理論値と実測値をグラフ化

25個の方が現実にあてはまっていると思う。
総裁選で所得倍増をいいながらやろうとしているのは軍事費倍増の詐欺に騙されたのが日本国民。
>>808 チンパンジーには問題になってないという日本語すら理解できないか
∫[0,1] {Σ[k=1,n] kx(e^kx)} dx
を求めよ。
>>807 話大とか文章からアホさが滲み出てて草
やっぱ話し通じないチンパンジーみたいだね
実際はシゾ患者だけどw
>>812 Zはユークリッド整域である
ガウス整数環Z[i]もユークリッド整域である。
体上の多項式環はユークリッド整域である。
I={0}の時、単項イデアルである
I≠{0}の時、N(a) (a∈I、a≠0) は空でない部分集合なので絶対値最小のものが存在する。Iは単項イデアルであり、Rは単項イデアル整域である。
>>813 今日もコロナ感染後の患者に挿管してベンチレーターにのせた。
「学習歴のアップデートを」 1科目から学び直せる制度、学位取得も
https://www.asahi.com/articles/ASQD96GYKQD9UTFL01H.html 「学びなおせる」ということは、まだ大学に入ったことのない高校生は
門前払いなのかな?
前
>>791 >>730訂正。前の答案を使わずに直接ちゃんと掛けて足して解くと、
0×5×0.1+1×5×0.1+2×18×0.1+3×14×0.1+4×7×0.1+5×1×0.1=0+0.5+3.6+4.2+2.8+0.5=11.6
∴12個
正規分布の本質は何でしょうか
なぜ測定の誤差が正規分布に従うのか
二項分布の極限みたいなイメージでしょうか
測定誤差も慎重の分布も世の中の現象は細かい2択の積み重ね的な解釈無いですか
n個の区別できないボールをm個の区別できない箱に1個ずつ無作為に投げ入れる。
(1)ちょうどk個(0≦k≦n)のボールが入っている箱が1つ以上存在する確率P(n,m)をn,mで表せ。
(2)mを固定してnを動かすとき、P(n,m)の最大値をmで表せ。
(3)P(n,m)の平均を求めよ。
昨日、コロナ患者の急変で気管挿管して人工呼吸器管理することになった。
https://www.niid.go.jp/niid/ja/2019-ncov/2551-cepr/10903-b11529-period.html によれば
オミクロン株症例の潜伏期間の中央値は2.9日(95%信頼区間:2.6-3.2)
という。
N=35とサンプルサイズが小さいのでグラフから生データを読み取って
bootstrapで計算してみた。
中央値
> median(b$t)
[1] 2.971429
Intervals :
Level Normal Basic
95% ( 2.671, 3.276 ) ( 2.686, 3.286 )
Level Percentile BCa
95% ( 2.657, 3.257 ) ( 2.629, 3.257 )
Calculations and Intervals on Original Scale
でガンマ分布を仮定した値と遜色ない。
1日経過したが、発熱や呼吸器症状はない。
気管挿管操作で感染する確率は不明ないので一様分布を事前分布に設定して
自分が感染している確率の95%信頼区間を求めたみた。
> f(1)
lower upper
0.05318045 0.99939996
濃厚接触からの時間が短いので信頼区間幅が広いのは仕方がないな。
>>824 自分自身を要素として持たない集合の集合は存在しますか?
>>824 尿瓶ジジイ性懲りも無く高校生にもバカにされに来たか
>>824 こんなけ長い時間ブートストラップとか言ってるくせにまだブートストラップとは何か、どういう意味があるのか理解できてないチンパンジー
そもそも尿瓶が参考資料とか言って貼ってたリンクの先の文章がそもそもダメダメやからな
それがダメダメだともわからない
なーんもわからない
>>821 実数を正と負に分けられるのが
本質とするか分類すると考えるか
∫[0,∞] e^(-st)f(t) dt =s/(1+s^2)
を満たす微分可能な関数f(t)はただ1つに定まることを示せ。
金曜日にスポット麻酔の依賴あり。
日曜日にコロナ患者(正確にはクラスター発生病棟の担癌の入院患者でPCR陽性の患者)の急変で気管内挿管したので自分が感染しているかもしれない。
https://www.niid.go.jp/niid/ja/2019-ncov/2551-cepr/10903-b11529-period.htmlの
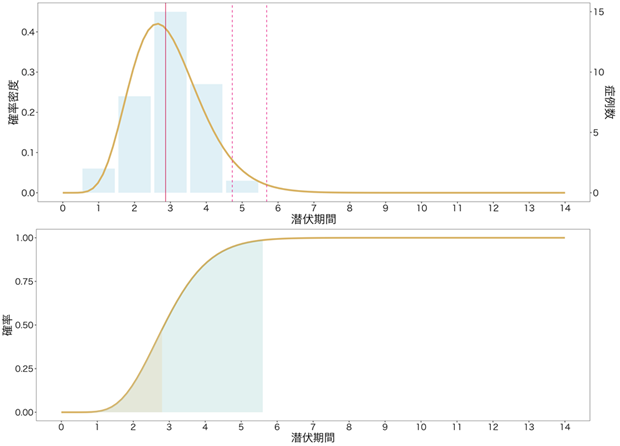
のデータを使って金曜日までに自分が発症しなかった場合に自分が感染している確率を求めたい。
ヒストグラムの潜伏期1日は1.00~2.00日を1日とカウントしたとして実測値と適合する分布を計算。

残渣平方和が最小になるのはweibull分布であったので、これを潜伏期の分布として採用。
挿管操作で感染する確率は不明なので一様分布を仮定。
5日間無症状であった場合に自分が感染している条件付き確率をベイズの公式と乱数発生させて計算。

lower upper
0.000 0.382
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000011 0.0109166 0.0311482 0.0844716 0.0891361 0.9997670
中央値が5%未満なので金曜日までに発症しなければ依賴を受けると返事をした。
そもそもスポット麻酔なんか他の医師に依頼なんかしないという事ですな
もういう事がメチャクチャ
a,bの正負を判定せよ。
a+2b=-1
ab=-1
√4+2√3という二重根号の問題で、
中を3+2√3+1に変えたら答えの√3+1に出来ますが、中全体を(4+2√3)^2とそのまま二乗しても同じ答えに出来ません。これはなにが原因でそうなっているのでしょうか…
>>835 (√3+1)^2=3+2√3+1=4+2√3
できるやん
関数f(x)はx>0で正の値をとる増加関数で、
f(2x)/f(x)→1 (x→∞)を満たすとき
任意の正の定数aに対し、f(ax)/f(x)→1 (x→∞) が言えますか?
f(2x)/f(x)→1 (x→∞)より
f(4x)/f(x)=
(f(4x)/f(2x))(f(2x)/f(x))→1 (x→∞)
・・・
であることと
f(x)が増加関数であることより明らか
f(2^n*x)/f(x)=Π[k=1,n]{f(2^k*x)/f(2^(k-1)*x)}→1(x→∞) より明らか
>>841 増加関数であることを使わないと導けない。
m個の区別できない箱に、n個の区別できないボールを1つずつでたらめに投げ入れる。
ボールが一番多く入っている箱をA、ボールが一番少ない箱をBとする。
Aに入っているボールの数をx、Bに入っているボールの数をyとするとき、x-yの期待値をm,nで表せ。
>>840 >>841 ありがとうごます。
これで2の累乗のときにいえるのはいえると思うますが
任意の正のaについていえるのは示されてませんのでは?
>>842 使ってるよ
a>1のとき f(x)<f(ax)<f(2^n*x)なるnがあり 1<f(ax)/f(x)<f(2^n*x)/f(x)→1
a<1のとき f(2^-m*x)<f(ax)<f(x)なるmがあり 1>f(ax)/f(x)>f(2^-m*x)/f(x)→1
>>836 回答くださりありがとうございます。
√(4+2√3)をわざわざ√(3+2√3+1)に変えて、
√(√3+1)^2にしてからルートはずして√3+1と導出するのと、
√(4+2√3)^2にしてそのままだして
√3+1にするのは同じと思って良いのか良く分からなくなってしまいまして…
初めて質問させて頂きます
よろしくお願いします
数学1 二次関数の範囲です
f(x)=x^2-2(a+3)x+1≧0が0≦x≦2の範囲で成り立つ時にaの範囲を求める問題です(画像一枚目)
参考書の類題(画像2枚目)は解けるので同じようなやり方で過去問やってたのですが答えが導けません
方程式が平方完成出来なさそうなので頂点の公式から軸を出して
変域より左、変域内、変域より右に頂点がある場合の最小値を出して最後にaの範囲を合わせて解けると思ったんですが…
解説がないので
どこが間違えてるのか解説してもらえないでしょうか
問題文は画像三枚目、解答は上から2 1 5 4 2になります



1
1≧0はaが何でも成り立つからa<-3
2
-4≦a≦-2かつ-3≦a<-1だから-3≦a≦-2
3
a≦-7/4かつ-1≦aだから条件を満たすaはない
①a<-3のとき 成り立つ (なぜか考慮されてない)
②-3≦a<-1のとき -4≦a≦-2 だから -3≦a≦-2 (aの上限が-1になってる)
③-1≦aのとき a≦-7/4 だから これを満たすaはない(なぜか-1≦aとなっている)
まとめると ①または②↔a<-3または-3≦a≦-2↔a≦2
>>851>>852
本当だ…なんでこんなミスしていたんだろう…
過去問なので焦って解いてしまってたようです
しっかり数直線を書いて考えれば分かったはずなのに申し訳ございません
ありがとうございます
また質問するかもしれませんがその際はよろしくお願いします
>>848 二乗したらソレになる数を探してるときにソレを二乗しても仕方ない
>>818 正規分布は定義域が-∞から+∞だから、現実に正規分布に従う確率変数は少ない。
あてはまるのは誤差くらいだな。
コロナ患者に挿管して3日め、自宅で経過観察中。
SARS-CoV-2の変異株B.1.1.529系統(オミクロン株)の潜伏期間の推定:暫定報告
https://www.niid.go.jp/niid/ja/2019-ncov/2551-cepr/10903-b11529-period.html のデータを使って計算。
潜伏期は日単位の離散量でなく連続量として、AICが最小となる分布を求めると
weibull分布がAIC最小になるのでこれで計算。
感染していた場合に今日中に発症する確率を計算すると、
> latancy_covid(4)-latancy_covid(3)
[1] 0.4276189
感染していた場合に今日、発症する確率は約4割となった。
コロナ患者への挿管操作で感染する確率は不明なので一様分布を仮定して計算する。
n日間発症しなかった場合に感染してる確率をベイズの公式と一様分布乱数を使って計算。
> calc(3)
lower upper
0.000 0.931
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000091 0.1922966 0.4177034 0.4440708 0.6833137 0.9999970
> calc(4)
lower upper
0.000 0.845
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000037 0.0876011 0.2243775 0.3026174 0.4652846 0.9999927
> calc(5)
lower upper
0.000 0.376
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000004 0.0105104 0.0310122 0.0840506 0.0878141 0.9999338
>>844 んで、あんたシリツ卒なの?
再受験すればいいのに。
理Iから理III再受験した眼科医もいるぞ。
>>844 医師が羨ましくて医師板に出入りするくらいなら、再受験でもすればいいのに。
俺の同期は2割くらいは再受験組だったぞ。国府台での教養時代には学卒者用の体育があった。
野球のメンバーが足りないので俺も参加していた。
当時は阪大には学卒入学制度があったから、再受験組は東大か京大卒だったな。
歯学部には東大数学科卒もいた。
高校生諸君は、>827みたいな助言ではなく罵倒しかできないようなクズ人間になっちゃだめだぞ。
数学板には助言より罵倒を喜びとする輩が多いね。
>>832 週1の大学からの麻酔科医派遣だけではまかなえないと俺にかつての同僚からスポット麻酔の依賴がくる。
ワクチン接種バイトよりもスポット麻酔の方が安全、接触する人数が最小限ですむ。
予定手術なのでコロナ陰性確認済だし、各種モニターも蘇生に必要な器具や薬剤も手元にある。
スレチの業界ネタだが、
スガマデックスでのアナフィラキシーには要注意だな。俺はスガマデックス静注後は15分はオペ室でバイタル安定を確認してから退室させている。
>>847 省略せず書けばこのように使ってるよ に訂正するわ
http://2chb.net/r/hosp/1668999699/ はい、コピペ
高校生諸君には5chで発狂するしか能がない哀れな老人にはなってほしくないなぁw
>>860 「求麻酔科バイト」はいくらでもあるけど「麻酔科でなくても桶」は流石に見つからないなwwwwww
>>858 そりゃアンタのことだろ
本気で自分のこと医者だと勘違いしてるシゾ患者なのか?
こちらの問題18なんですが
y=x^2+2ax+9に判別式D<0を使うと
(2a+6)(2a-6)<0
-3<a <3
となってしまいます
解答は③だったんですが解き方間違ってますか?

頂点は(-a,-2a+1)だがx軸との交点を持たないからこのy座標が正
y軸とy=9で交わるって話とx軸と交わらないって話は別の話だな
条件のいいバイトは個人的なコネでくるからね。
気心の知れたかつての同僚の依頼は断りにくい。
まあ、PCR陽性患者の麻酔はCt値不明だったのでお断りした。
それでも次の依頼がくる。
鼠径ヘルニアは点数が丸めなので高額のブリディオンなしで抜管できるように麻酔している。ブリディオンはアナフィラキシーの頻度も高いのもあるし。
こういうのが業界ネタ。
>>869 再受験する気概もない椰子が延々と医師が羨ましいという投稿を続けているからなぁ
んで、あんたシリツ卒なの?
不定積分と原始関数の違いが分かりません。違いをどうぞ説明してください。
あと、微分可能と積分可能って違うんですか?
まぁわざと同じこと繰り返して「相手が何言ってきてもオレ様止める事はできない、オレ様すごい」とでも思いたい小学生の知能なんやろ
60年以上色んな事見聞きしてきてその結末がコレ
人間になり損ないの肉の塊
>>871 >不定積分と原始関数の違いが分かりません。違いをどうぞ説明してください。
厳密に定義されてるのかしらん
不定積分は区間が限定されてない定積分で
原始関数は微分の逆
こんな程度の理解デいいじゃね?
>>858 勘違いしているようだが、そもそも数学板の皆様は一ミリも医者にはなりたくなかったのではないか?
至るところ微分可能だが、一部区間で積分不可能な実数値関数fは存在しますか?
数直線も一部区間の一部
開区間(a,b)上いたるところ微分可能な関数は
区間(a,b)に含まれる有界閉区間上で
積分可能
連続関数f(x)は、f(0)=1であり、また任意の実数a,bに対して
f(a+b) - f(a-b)=2f(-a)sin(b) を満たす。
(1) f(x)は微分可能であることを示せ。
(2) f(x)を求めよ。
連続関数は微分可能じゃないのですか。
とんがってるとこは右微分係数と左微分係数が一致しないから
とすると
微分可能ということを示すにはなにをいえばいいんのでしょうか
定義域の全てで右微分係数と左微分係数が一致することを微分の定義に遡って示せばいいんじゃね
知らんけど
>>微分可能ということを示すにはなにをいえばいいんのでしょうか
f(x)が0で微分可能であることを示すには
lim_{x\to0}{\frac{f(x)-f(0)}{x}}が存在することを言えばよい。
f(a+b) - f(a-b)=2f(-a)sin(b)
{f(a+b) - f(a-b)}/(2b)=f(-a){sin(b)/b}
連続だからlim[b→0]右辺=f(-a)lim[b→0]{sin(b)/b}=f(-a)
右辺の極限があるから左辺の極限もあってf'(a)=f(-a)
f(0+b)-f(0-b)=2f(-0)sin(b)
f(b)-f(-b)=2sin(b)
f'(b)+f'(-b)=f(-b)+f(b)=2cos(b)
f(b)=cos(b)+sin(b)=√2sin(b+Π/4)
コロナ患者に挿管して5日が過ぎた。
明日発症する確率を計算*)
Median Mean
0.0003615 0.0026553
で中央値、平均値とも1%未満になった。
95%信頼区間は
ower upper
0.000 0.007
*)
https://www.niid.go.jp/niid/ja/2019-ncov/2551-cepr/10903-b11529-period.html のデータを用いて潜伏期は日単位の離散量でなくて連続量として
潜伏期間の確率密度関数を計算するために、
観察された潜伏期間に対してGamma分布, Lognormal分布, Weibull分布のあてはめを検討し、
Akaike Information Criterion(AIC)による比較で最も当てはまりが良かったGamma分布を採用して確率密度分布を算出した。
を行うとWeibull分布のAICが最小になった。
>>876 外科は引退したから、麻酔や内視鏡以外は脳内業務が多いな。
病棟で小ナートや顎関節脱臼整復くらいはする。
麻酔の投薬量もプログラム組んで計算させている。
たまに体重が2kg程減ったりしていることもあるが、スマホで再計算できるのでその場で再計算してる。
こんな出力。チューブの固定位置とか人工呼吸器の初期設定も表示するようにして改訂した。
> Anesthesia(174,53,35,male=F,Sevo=TRUE,propofol = TRUE,japanese=TRUE)
BMI = 17.51
Ideal Body Weight(kg) = 66.61
Body Weight @ BMI25(kg) = 75.69
Lean Body Mass(kg) = 42.98
Propofol(mL) in bolus = 8.12 / 16.25 - 20.31
injection speed = 0.41 mL/sec
Remifentanyl (0.25μg/kg/min, 1μg/kg)
continuous(mL/h) = 7.86
bolus(mL) = 0.52
CE(ng/mL)@(1mL/h)= 0.97
cf. Ultiva(BMI25,aged70) (mL/h) 7.95 - 15.9
Rocuronium
bolus(mL) = 3.18 - 4.77
continuous(mL/h) = 0.95 - 1.27
Sevoflurane(%)
MAC 2.17
maintenance 1.33 - 1.44
Incisor to Tracheal MidPoint = 22.4 cm
Tidal Volume = 521 Respiratory Rate = 12
>>886 よくわからんけど
「悠仁殿下が4回目の摂取をした」
って発表があったら起こしてくれ。
ワイもワクチン摂取するけん。
>>887 はいはい、脳内医者ワロス
一体誰が信じるんだろうね、アンタみたいなシゾ患者のぬかすことなんざ
231kgから170kgに15.5秒かけて質量が目減りする物体の加速度を計算して終速度と距離を計算したいんですけどこの目減りしていく質量はどう計算に組み込めば良いんでしょう
コンマ1秒毎に155回計算すれば良いんでしょうけど流石に面倒で
>>885 lim[b→0]{f(a+b) - f(a-b)}/(2b) が存在するからといって
まだf(x)がx=aで微分可能といえなくない? 必要だけど十分じゃない。
あくまで lim[b→0]{f(a+b) - f(a)}/(b) が存在することをいわないと。
>>893 推力5750lbfの飛翔体になります
固定重量での飛距離は計算出来るのですが軽くなった分増すはずの加速度を加味した飛距離を求めたく
よくわからんけど推力Fが一定だほかに何も力がかかってないなら
F = mv' = (m₀-μt)v'
だから
v = ∫F/(m₀-μt) dt
じゃないの?
前
>>817 >>891 61kgはライト級だよ。134lb強だら。
133+3/4で試合したことあるもんで。
飛翔しながら減る奴おるか知らんけど、
比推力ってやつを考えると、
5750÷{(61/0.454)/15.5}=633.323770492……(s)
60で割って約11分3秒
あとはエネルギー保存の法則と運動量保存の法則ぐらいか。
>>892 (f(a+b)-f(a))/b=g(b)と置くと
{f(a+b) - f(a-b)}/b=g(b)+g(-b)=2f(-a){sin(b)/b}
右極限を取ると
lim[b→+0](g(b)+g(-b))=lim[b→+0]g(b)+lim[b→-0]g(b)
=lim[b→+0]2f(-a){sin(b)/b}=2f(-a)だから
f(a)の左右微分の平均=f(-a)
f(b)-f(-b)=2sin(b)
両辺で右微分すると
f(b)の右微+f(-b)の左微分=2cos(b)
両辺で左微分すると
f(b)の左微分+f(-b)の右微分=2cos(b)
平均を取ると
f(b)の左右微分の平均+f(-b)の左右微分の平均=f(-b)+f(b)=2cos(b)
2f(b)=2sin(b)+2cos(b)
f(b)=√2sin(b+π/4)
f'(b)=√2cos(b+π/4)
>>889 医師が羨ましいなら再受験でもすればいいのに。
俺の医科歯科の同期は2割くらいは学卒だったぞ。
大半は東大か京大卒。当時は阪大医学部には学士入学制度があったから阪大卒はいなかったな。歯学部には東大数学科卒もいた。
新潟大学には看護助手から医師になった人もいる。
>>898 医師が羨ましいのはアンタだよ
もっともアンタは患者だけどな
(a,b)。
f(a+b)-f(a-b)=f(-a)g(b)。
(x/2,x/2)+(0,x)-(-x/2,x/2)-g(x/2)(0,x/2)。
f(x)=f(0)(2-g(x/2)^2+g(x))/2。
>>880 a=x+h, b=h として
f(x+2h)-f(x)=2f(-x-h)sin(h)
h≠0として両辺2hで割ってh→0の極限とれば 右辺はf(-x)に収束するおで導関数が存在
f(x)=x^3+ix^2+ax+1
とする。ただしaは実数の定数、iは虚数単位である。
(1)方程式f(x)=0が持つ実数解の個数を求めよ。
(2)方程式f(x)=0が持つ純虚数解の個数を求めよ。
x^3+ix^2+ax+1=0
ix^2+(x^3+ax+1)=0...(*)
xが実数のとき、x=0が必要
しかしそのとき(*)は成り立たない
よって(1)は0個
xが純虚数x=it(tは実数)のとき、
(-i)*t^3-it^2+iat+1=0
i(-t^3-t^2+at)+1=0
左辺の実部は1,右辺の実部は0よりこの等式を成り立たせるtはない
よって(2)は0個
>>904 それは白髪まじりのおっさんが すでに素晴らしい回答をして本を出している
係数および定数項が複素数の3次関数f(x)で以下の性質をすべて持つものは存在するか。
・任意の実数tに対してf(t)は実数でないか0である
・実数でない任意の複素数αに対してf(α)は実数である
積分の仕組みはコレだ!
・輪っかの長さ を 積分すれば ピザの面積が得られる!
・ピザの面積 を積分すれば トグロうんこの (円錐の) 体積が得られる!!
↑ これで君も積分マイスター銀バッジ だ!
tana=1/5 tanb=1/239 のとき
tan(2a)=2/5/(1-1/25)=10/(25-1)=5/12
tan(4a)=10/12/(1-25/144)=120/(144-25)=120/119
tan(4a-b)=(tan(4a)-tanb)/(1+tan(4a)tanb)
=(120/119-1/239)/(1+120/119/239)=(120*239-119)/(119*239+120)=1
4a-b=π/4だから4arctan(1/5)-arctan(1/239)=π/4
arctanx=∫[0,x]dt/(1+t^2)
xが正のとき右辺の分母のtをxに置き換えると減少し0に置き換えると増加するから
x/(1+x^2)<arctanx<x
1/5/(1+1/5^2)=5/26<arctan(1/5) arc(1/239)<1/239
π/4>4*5/26-1/239=10/13-1/239=2377/3107 π>9508/3107>3.06
a,b,cは実数とする。
x^3+ax^2+bx+c=0
が相異なる3つの解を持つとする。
(1)解の1つは実数であることを示せ。
(2)3つの解が複素数平面上の原点を中心とする同一円周上にあるとき、a,b,cが満たす必要十分条件を求めよ。
実数a,b,cは
0<a≦b≦cかつa^2+b^2>c^2をみたす。
p,q,rを
p=a^2+b^2-c^2
q=b^2+c^2-a^2
r=c^2+a^2-b^2
とおくとき、以下の問いに答えよ。
(1)p,q,rは正であることを示せ。
(2)p+r>qとなるための、a,b,cが満たすべき必要十分条件を求めよ。
(3)p,q,rをそれぞれ3辺の長さとする△PQRが存在するとき、その面積をa,b,cで表せ。
5つの辺の長さが1で、残り1つの辺の長さがaである四面体が存在するための実数aの条件を述べ、その体積を求めよ。
>>898 脳内医者のアンタには誰が医者になろうが関係ないだろマヌケ
せいぜい便所の落書きで発狂してろや
>>907 塾講師や家庭教師の人は
このネタを使っていいぞ ( '‘ω‘)b
aを正の実数の定数、b,cを実数の定数とする。
-1≦ax^2+bx+c≦1を満たす実数xが存在するための、a,b,cの満たすべき必要十分条件を求めよ。
>>907 循環論法を避けるために三角関数の極限を使わずに円の面積を求める方法の一つだと思うんだけど
円周を半径で積分すれば面積得られるよね
>>915 一般化するには円周から円盤でなく円盤から円周に微分でと考えた方が良いよ
その上で
線分から円盤
円盤から球体
球体から…
と次元上げていくのが良い
円周から球面は面倒
以下のように商品Bがクーポンで0円だったと仮定した場合の返金額の計算をしてみたのですが、AとBに対するクーポン適用額が固定されている場合、返金額の補填で購入者の損失を埋めることはできませんよね?
ストア側がクーポン1200円をそれぞれの商品に自動適用
商品A 金額2268円 クーポン813円適用して1455円
商品B 金額1074円 クーポン387円適用して687円
総額3342円のところ1200円のクーポンが適用され、購入者は2142円を支払う
購入者の手元に届いた商品Aが破損していたため返金手続きを行う
返金額は1455円になる
もしもBに対してクーポンが全額適用されていたら
商品A 金額2268円 クーポン126円適用すると2142円
商品B 金額1074円 クーポン1074円適用すると0円
この場合、Aの返金額は2142円となるため、1455円返金では購入者に687円の損失が生まれる
なのでAの返金額1455円に加えて687円を請求して2142円とする
しかしBは購入されるわけだから、A(1455+687)+B(687)=総額2829円になり、ストア側に687円の損失が生まれてしまう
 >>914
>>914 aが正なのでy=ax^2+bx+cのグラフは下に凸
の放物線.だから、a>0の下で
「-1≦ax^2+bx+c≦1を満たす実数xが存在する」
⇔「ax^2+bx+c=1を満たす実数xが存在する」
⇔「ax^2+bx+(c-1)=0の判別式が0以上」
⇔ b^2-4a(c-1)≧0
⇔ b^2≧4a(c-1)
って感じだと思う.(心配なら最終的な答えに"a>0"って書いたら親切かな?)
間違えたりしてたら申し訳ないのと,
5ch初レスだからなんか色々不安
 >>911
>>911 イメージとしては「◀▶みたいに正三角形2つを一辺を共有するようにとる.正三角形Aと正三角形Bの角度(二面角?)を変えたとき,正三角形でそれぞれ唯一共有していない点同士を結んだ辺の長さがa.それの取り得る値の範囲を求める.」
って感じになるかな.
《解答》
5つの辺の長さは1であることから,四面体が出来るときは正三角形の面が2つできる.それを正三角形ABCと正三角形BCDとおく.(共有する辺はBC)
ADの長さがaに当たるから,このaの取り得る範囲を求めればよい.
BCの中点をMとする.∠AMDは0°より大きく180°より小さい角度をすべて取り得る.i.e. -1<cos∠AMD<1の全ての範囲を取り得る....①
a=(AM)^2+(DM)^2-2(AM)(DM)cos∠AMD
=(3/4) + (3/4) - 2 (3/4)× cos∠AMD
= 3/2 - 3/2 × cos∠AMD
よって,これと①より,
0<a<3が答え.
BCの中点をMとしてからは,aが0より大きく(2×MD)より小さい全ての値を取るのを自明としても怒られないんじゃないかな?
∫{x^3+sin(x)}^2 dx
の簡単な計算方法ってないですか?
素直に部分積分すると計算量が多くて萎えます
f(0)=f(1)=0
0<x<1でf"(x)<0, f(x)>0
を満たす0≦x≦1で連続な関数f(x)について
0<x_1<x_2<1で x_2-x_1=f(x_1)=f(x_2)となるx_1, x_2がが存在することを示せ
これの解法がわかりません…
>>923 中間値の定理やろ
上に狭義凸だからある0<x₀<1で0≦x≦x₀で狭義単調増大、x₀≦x≦1で狭義単調減少だから0≦x₀≦1でのfの逆関数g(y)とx₀≦x≦1でのfの逆関数h(y)が存在する、定義域は共に0≦y≦f(x₀)、y₀=f(x₀)とする
関数φ(y) = h(y) - g(y) - yとおげばφ(y)は狭義単調減少で
φ(0)=1-0-0 = 1 > 0
φ(y₀) = x₀-x₀-y₀ < 0
だからいずれかのcでφ(c)=0
この時x₁=g(c), x₂=h(c)が求める条件満たす
>>922 (sinx-xcosx)'=xsinx などなど
>>909 x^3+ax^2+bx+c=0 の左辺はxを大きくすればいくらでも大きくできて
xを小さくすればいくらでも小さくできるので中間に零点があるのは明らか
三つの解をp,q,rとすし少なくとも一つある実数解をrとする
p,qも実数のとき、これらの絶対値はrのそれと同じだから、(p,q)=(r,r),(r,-r),(-r,-r)
-a=p+q+r=3r,r,-r
b=pq+qr+rp=3r^2,-r^2,-r^2
-c=pqr=r^3,-r^3,r^3
より、b^3=ca^3
p,qが虚数のとき共役だからpq=r^2
-a=p+q+r だから p+q=-a-r
b=pq+qr+rp=r^2+r(-a-r)=-ar
-c=pqr=r^3
b^3=-a^3*r^3 だからどちらにせよ b^3=ca^3
>>910 a,b,cの大小関係からq≧r≧pで、条件よりpは正だからすべて正
p+r=2a^2 だから p+r>q↔3a^2>b^2+c^2
三辺がx,y,zの三角形の面積をS、x+y+z=2L 二つの辺のなす角をtとすると
cost=(x^2+y^2-z^2)/(2xy) だから
1-(cost)^2=(1+cost)(1-coat)=((x+y)^2-z^2)(-(x-y)^2+z^2)/(2xy)^2
=(x+y+z)(x+y-z)(-x+y+z)(x-y+z)/(2xy)^2
=2L(2L-2z)(2L-2x)(2L-2y)/(2xy)^2=4L(L-x)(L-y)(L-z)/(xy)^2
4S^2=(xysint)^2=(xy)^2(1-(cost)^2)=4L(L-x)(L-y)(L-z) だから
S=√{L(L-x)(L-y)(L-z)}
△PQR=√{(a^2+b^2+c^2)(3a^2-b^2-c^2)(3b^2-a^2-c^2)(3c^2-a^2-b^2)}/4
x^3+x^2=x^2(x+1).
x^3+7x^2+14x+8=(x+1)(x+2)(x+4).
(pq+pr+qr)^3-pqr(p+q+r)^3=(qr-p^2)(pr-q^2)(pq-r^2).
立方体の展開図は11種類ありますがでは面の区別までした展開図は何通りあるでしょうか
例えば1つのさいころを展開したとき展開図上の目の配置で何通りかの区別がつく展開図ができますね回転裏返しで重ならない展開図の総数は何通りでしょうか
実数a,b,cに対して
a/(1+a^2) + b/(1+a^2+b^2) + c/(1+a^2+b^2+c^2) < √3 を示せ
お年玉問題なのですがこれは高校生でも解ける問題ですぅか
2c<=1+c^2<=1+a^2+b^2+c^2.
入試問題で答えを複素数αを用いて表せ、と指定されたときαの共役複素数αバーも使っていいと判断して良いですか?
nを正整数とする。
√{n+√(n)}+√{n-√(n)}
は無理数であることを示せ。
√{n+√(n)}+√{n-√(n)} を平方すると n+√(n)+n-√(n)+2√{n^2-n}
しかし n^2-2n+1<n^2-n<n^2 だからn^2-nは平方数でなく√{n^2-n}は無理数
間違えた
n=1のとき √2だから無理数
n>1のとき n^2-2n+1<n^2-n<n^2
それは整数でない事示してるだけやろ
高校数学なら「代数的整数かつ有理数なので整数」は使えない
でもまぁ「平方数でない整数の平方根は無理数」はさすがに許してくれるかな?
連立方程式
y=2x^2
(x-1)^2+(y-1)^2=1
は実数解を2つと、互いに共役な複素数解を1つずつの、計4つの相異なる解を持つことを示せ。
(x-1)²+(x²-1)-1=0
はy=x²と(x-1)²+(y-1)²=1が公差している2つの共有点をもつから重解でない異なる実数解をちょうど2個持つ
よって(x-1)²+(x²-1)-1は異なる一次の因子2つと実係数の2次の因子をひとつ持つ
二次の実係数の因子は解の公式により共役な複素数解を持つ
(y-1)^2-1=(2x^2-1)^2-1=2x^2(2x^2-2)=4x^2(x+1)(x-1) だから
0=(x-1)^2+(y-1)^2-1=(x-1)^2+(2x^2-1)^2-1
=(x-1)(x-1+4x^2(x+1))=(x-1)(4x^3+4x^2+x-1)
4x^3+4x^2+x-1について
x=-1/2のとき-1でx=1のとき8だから中間に零点がある
x=-1/2のとき極大だがそれは負だから実根は-1/2と1の間に一つだから示された
(y-1)^2-1=(2x^2-1)^2-1=2x^2(2x^2-2)=4x^2(x+1)(x-1) だから
0=(x-1)^2+(y-1)^2-1=(x-1)^2+(2x^2-1)^2-1
=(x-1)(x-1+4x^2(x+1))=(x-1)(4x^3+4x^2+x-1)
4x^3+4x^2+x-1について
x=-1/2のとき-1でx=1のとき8だから中間に零点がある
x=-1/2のとき極大だがそれは負だから実根は-1/2と1の間に一つだから示された
実数a,b,c,d,eに対して
a/(1+a^2) + b/(1+a^2+b^2) + c/(1+a^2+b^2+c^2)
+d/(1+a^2+b^2+c^2+d^2) + e/(1+a^2+b^2+c^2+d^2+e^2)< √5 を示せ
お年玉問題なのですがこれは高校3年生でも解ける問題ですか
xy平面上の単位円C:x^2+y^2=1に内接する正三角形Tがある。
Tの1つの頂点の座標が(a,b)、b=√(1-a^2)であるとき、残りの頂点の座標をaで表せ。
nを正整数の定数とする。
n*e^(x)-(n^2)*(1+x)<0
をみたす実数xが存在するかどうか調べよ。
y=sin(x)の0≦x≦πの部分の長さと、2πの大小を比較せよ。
a[1]=1,a[2]=1
a[n+2]=a[n+1]a[n]+1
で与えられる数列{a[n]}を考える。
k=1,2,...n-1に対し、a[n]をa[k]で割った余りをnとkで表せ。
I[n]=∫(x^n){e^(-x)}dx
とおく。
(1)I[0],I[1]を求めよ。
(2)I[n+1]をI[n],I[n-1],...I[0]のうち必要なものを用いて表せ。
0≦x≦y≦z
0≦xy+yz+zx≦1
のとき、
(1+x)(1+y)(1+z)
の取りうる値の範囲を求めよ。
実数xの写像f(x)、g(x)ってのがあったとして
f(x)をg(x)で微分することって必ずできる?
それともf(x)=h(g(x))とか表すことができなければ無理?
例えば
f(x)=x^2、g(x)=x^3
とかなら
f(x)=(x^3)^(2/3)とかすれば微分できそうだけど
f(x)=exp(x),g(x)=tan(x) (-π/2<x<π/2)
みたいにぱっと見相互に表せなさそうなのって
f(x)をg(x)で微分ってできるのかなって
>>958 >f(x)をg(x)で微分する
定義して
df(x)/dg(x)={df(x)/dx}/{dg(x)/dx}
=exp(x)/(1/(cosx)^2)=exp(arctan(g(x)))/(1+(g(x))^2)
>>952 複素平面でe^(it))、e^(i(t+3/2*π))、e^(i(t-3/2*π)) の三つが頂点だから
a=cost、b=sint のとき残りは (a+ib)(-1±i√3)/2=-a/2-±b√3/2±i(a√3/2-b/2)
だからxy平面で (-a/2-b√3/2,a√3/2-b/2),(-a/2+b√3/2,-a√3/2+b/2)
∫[0,π]√(1+(cosx)^2)dx<∫[0,π]√(1+(cos(0))^2)dx=√2π<2π
>>953 n*e^(x)-(n^2)*(1+x)<0 両辺nで割って e^(x)-n*(1+x)<0
n=1のとき e^xは下に凸でその接線が1+xだから成り立たないので存在しない
n>1のとき x=0のとき1-n<0だから成り立つので存在する
速度vがある
時間t=e^sとする
vをtではなくsの関数で表せ
お願いします
>>955 nを0以上、a[0]=0とし a[n]をa[k]で割った余りはa[nをkで割った余り] を示す
n<kのとき明らか n=k,k+1,k+2のときも成り立つ
n≦k+m+1のとき成り立つと仮定する
a[k+m+2]=a[k+m+1]a[k+m]+1 この右辺をa[k]で割った余りは
a[m+1をkで割った余り]a[mをkで割った余り]+1
=a[mをkで割った余り+1]+a[mをkで割った余り]+1
=a[mをkで割った余り+2]=a[k+m+2をkで割った余り] だから成り立つ
I[0]=-e^(-x)
I[n]=-e^(-x)x^n+∫nx^(n-1){e^(-x)}dx=nI[n-1]-e^(-x)x^n
I[1]=I[0]-xe^-(-x)=-(x+1)e^(-x)
>>970 すみません。V(t)は与えられています
V(s)の求め方がわかりません
>>957 3x^2≦xy+yz+zx≦3z^2 より y,zともにxに等しくx=0のとき最小で1
x,yともにzに等しくz=1/√3のとき最大で(1+1/√3)^3
>>974 V(t)がvやcとしか与えられていないからです
時間の物差しをtからsに取り替えると
vやcをどう変形しなくてはならないでしょうか
>>967は
V(log(t))=V(s)
ということですかね
例えば
V(t)=c
だった時
V(log(t))=???
という質問です
>>975 関数概念の認識不足
vをtの関数v(t)で表すとき
vをsの関数v(s)とは表せない
>>960 g(a)→g(b)のときf(a)→f(b)と変化するはずだから
lim[]{f(b)-f(a)}/{g(b)-g(a)}になるのかなって
コーシーの平均値の定理見ててこういう式イメージしたけどそもそも定義されてないものなのか
>>978 関数を関数では定義されていまいな
それを定義にするなら
>>961 つまりf(x)=h(g(x))みたいに表せない場合はなくて
どんな場合においてもdf(x)/dg(x)はできるのかな
x=g^-1(g(x))とすればf(x)=f(g^-1(g(x)))になるから大体微分できちゃうのかな
このやり方はめちゃガバガバではあるけど
>>975 >時間の物差しをtからsに取り替えると
ってことは、v(t)=dx(t)/dtに対して、u(s)=dx(e^s)/dsを求めたいってことなんじゃないの?
だったら、合成関数の微分で u(s) = (dx/dt)(dt/ds) = v(e^s) e^s だな。
6面がすべて平行四辺形である6面体は
平行6面体といえますか・
>>950 上限を考えたいので各文字は正とする 題意の左辺の各項の分母を並べると
1+a^2
1+a^2+b^2
1+a^2+b^2+c^2
1+a^2+b^2+c^2+d^2
1+a^2+b^2+c^2+d^2+e^2
であるがこれらを A B C D E と置く
題意の左辺はベクトル(1/A,1/B,1/C,1/D,1/E)と(a,b,c,d,e)の内積である
前者のベクトルをP,後者をQとする
両ベクトルの長さが一定の下で後者が前者の正数k倍のとき内積は最大になる
そのケースで考えたいので Aa=Bb=Cc=Dd=Ee=kとする
B/A=b/a より aB=bA a(A+b^2)=bA ab^2-Ab+aA=0
判別式=A^2-4a^2A=A^2-4(A-1)A=A(-3A+4)
ゆえに0<A<4/3 さらにA>1だから 1<A<4/3 0<a<1/√3
k=Aa=(1+a^2)a=a^3+a
│Q│^2<5a^2 │P│=│Q│*1/K
│P│*│Q│=│Q│^2*1/K<5a^2*1/(a^3+a)=5/(a+1/a)
右辺の分母 a+1/a は0<a<1で減少なので下限はa=1/√3のとき
このとき右辺は 5/(√3+1/√3)=5√3/4=√(25*3/16)<√(80/16)=√5
題意の左辺=P・Q≦│P│*│Q│<√5
1辺の長さがaである立方体V:ABCD-EFGHを考える。
正方形ABCDの対角線の中点をMとする。
Vを直線GMに垂直な平面で切ったときの切断面の面積の最大値を求めよ。
またその平面とGMの交点をPとするとき、比GP/GMを求めよ。
Cを通る切断でもしその断面が四角であればそれが面積最大
ACGEで、ACの中点MとGを通る直線をlとする
lに直交しCを通る直線とAEとの交点をXとする
CA:AX=AG:GM=1:√2/2 AX=CA/√2=a=AE
XはEであったのでCEを通る面で切れば断面は四角になる
断面はひし形で長い方の対角線はCEで長さは√3a
短い方の対角線の長さは√2aだから断面積は√(3/2)*a^2
△GCM∽△GPC だから GM:GC=GC:GP
GP/GM=GC^2/GM^2=a^2/{√(1+1/2)a}^2=2/3
>>950 a,b,c,d,eを正とし、①どれも1/2を超えるとき
A=1+a^2>1+1/4=5/4
B=1+a^2+b^2>1+2/4=6/4
C=1+a^2+b^2+c^2=1+3/4=7/4
D=1+a^2+b^2+c^2+d^2>1+4/4=8/4
1/√A+1/√B+1/√C+1/√D<2/√5+2/√6+2/√7+2/√8<3.2だから
a/A=a/(1+a^2)=1/(a+1/a)≦1/2
b/B=b/(b^2+A)=1/(b+A/b)≦1/(2√A)
c/C=c/(c^2+B)=1/(c+B/c)≦1/(2√B)
d/D=d/(d^2+C)=1/(d+C/d)≦1/(2√C)
e/E=e/(e^2+D)=1/(e+D/e)≦1/(2√D)
題意の左辺=a/A+b/B+c/C+d/D+e/E
≦1/2*{1+1/√A+1/√B+1/√C+1/√D}<1/2*(1+3.2)=2.1<√5
②少なくとも一つは1/2以下であるとき
例えばeが1/2以下であれば
e/E=e/(e^2+D)=1/(e+D/e)≦1/(1/2+2D)<1/(1/2+2*1)=2/5だから
題意の左辺=a/A+b/B+c/C+d/D+e/E
≦1/2*{1+1/√A+1/√B+1/√C+2/5}<1/2*{1+1+1+1+2/5}
=1/2*4.4=2.2<√5 他の文字でも同様
lud20241207163925caこのスレへの固定リンク: http://5chb.net/r/math/1665137574/
ヒント:5chスレのurlに http://xxxx.5chb.net/xxxx のようにbを入れるだけでここでスレ保存、閲覧できます。
TOPへ TOPへ
全掲示板一覧 この掲示板へ 人気スレ |
>50
>100
>200
>300
>500
>1000枚
新着画像
↓「高校数学の質問スレ Part422 ->画像>37枚 」を見た人も見ています:
・高校数学の質問スレ Part410
・高校数学の質問スレ Part413
・高校数学の質問スレ Part421
・高校数学の質問スレ Part412
・高校数学の質問スレ Part416
・高校数学の質問スレ Part418
・高校数学の質問スレ Part437
・高校数学の質問スレ Part424
・高校数学の質問スレ Part436
・高校数学の質問スレ Part426
・高校数学の質問スレ Part429
・高校数学の質問スレ Part432
・高校数学の質問スレ Part414
・高校数学の質問スレ Part425
・高校数学の質問スレ Part427
・高校数学の質問スレ Part430
・高校数学の質問スレ Part433
・高校数学の質問スレPart404
・高校数学の質問スレPart407
・高校数学の質問スレPart397
・高校数学の質問スレPart406
・高校数学の質問スレPart403
・高校数学の質問スレPart408
・高校数学の質問スレPart400
・高校数学の質問スレPart407
・高校数学の質問スレPart405
・高校数学の質問スレPart404
・高校数学の質問スレPart401
・【あさひ】高校数学の質問スレPart397
・高校数学の質問スレ(医者・東大卒専用) Part438
・高校数学の質問スレ(医者・東大卒禁止) Part438
・高校数学の質問スレ(国立医・東大合格者専用) Part439 (10)
・数学の質問スレ
・高校数学の問題を出し合い解き合うスレ
・面白い高校数学の問題貼ってくスレ
・高校数学レベルの自作問題にチャレンジするスレ
・高校数学で質問があります
・高校数学のベクトルは何なの?
・いい感じの高校受験の数学の問題をくれ
・中学高校数学からやり直したい
・高校数学で最も難しい単元とは?
・高校入試の数学を教えてください
・高校数学 この問題解けたらアイス奢る
・高校数学難しすぎて笑うしかない
・高校の数学1が理解できないんだが....
・中学高校の教育に数学は必要あるか
・大学数学を極めたら高校で無双できるのか?
・高校数学ってどうすればいいですか?
・中学数学を100とした場合の高校数学の難易度
・高校数学に「データの分析」は必要?
・高校数学の「図形と方程式」とかいう名称
・高校数学はテイトモチーフって本当?
・高校数学飽きたから大学の数学すこし学びたい
・『データの整理』を高校数学に入れていいのか?
・文系卒おじさんだけど高校数学からやりなおす
・高校数学の範囲で究極に難しい体積計算の問題ってどんなものがある?
・高校生「数学が好きだから数学科行こ」←こいつw
・ユークリッド幾何学は中学・高校数学から撤廃すべき
・高校数学 バクテリアの増殖 わからん(´・ω・`)
・数学者を志す高校3年なんだけど、数学が理解できずにしんどい。
・鉄緑会では中3で高校数学を終えて入試までにハイレベル高校数学を3周する
・高校まで数学苦手だった人間が高等数学で何か成すって無理?
・高校生「数学(問題演習)おもしれw数学科行くわ」大学数学「理論の詰め込み教育です」←これ
16:47:06 up 70 days, 17:45, 0 users, load average: 12.26, 12.08, 12.55
in 0.037302017211914 sec
@0.037302017211914@0b7 on 062705
|






































