�ꉞ���Ă�����
�O�X���Ɉē������̊Ԃɍ�������B
�O�X��>913��
�O�X��>>988
> �����n�ƌ����Ă��鎞�_�ŌZ�̉����x�^����F�߂Ă����
> ���ꂪ���ꑊ�ΐ����_�̌��E
�Z���u��̌n = �����n�ɑ��āv�����^�����Ă���͎̂����Ȃ̂ŁA�F�߂�͓̂�����O�B��ʑ��Θ_���낤�����ꂾ�낤�������ς��Ȃ��B
�Z��̍��W�n�������Ȃ��Ƃ������Ƃ̍����ɂȂ�Ȃ��B
�����ČZ��̌n�͓��ꂾ�낤����ʂ��낤�������n�ł͂Ȃ��B
�O�X��>>997
> ��������ꑊ�ΐ����_�Ő����ł���Ȃ炵�Ă݂����
�O�X��>>961��
> ������W�n�Ō��ۂ��L�q�ł��Ă���Ƃ��ɁA�ʂ̍��W�n�ł��̌��ۂ��ǂ��L�q����邩�Ƃ����̂͏����ɐ��w�̖��
> �Ȃ̂ŁA�����n�Ō��ۂ��L�q�ł��Ă�̂Ɋ����n�ȊO�̍��W�n�ŋL�q�ł��Ȃ��Ȃ�Ă��Ƃ͂��蓾�Ȃ��B
�Ə������Ƃ���A
�����n�ł̌Z�A��̐��E���ƌŗL�������܂��Ă���̂�����A�Z��̂̍��W�n���߂āi�����h���[���W�n�₻��ɗނ�����W�n�j�A�����n�ł̌���
�����W�ϊ����邾���B ���Z�����ł悭�݂�����A�����W���čl����Ηǂ�
�܂��{�[���Ɏ��v������
�����ē��������v���������Z���{�[����������������
�����Ė߂��Ă����{�[���̎��v�ƌZ�̎��v���r����
�ǂ��炪�x��Ă��邩���ꑊ�ΐ����_�Ő����ł���Ȃ炷�����
���ꂪ�o�q�̃p���h�b�N�X�̌Z�̎��_��
������o�q�̃p���h�b�N�X�̐����ȂǓ��ꑊ�Θ_�ł�����ł�����Ă���[�́B
���ꑊ�Θ_�ł͉������W�������Ȃ��ƌ��߂��Ă���肱���ɂ͉i�v�ɗ����ł��Ȃ������̘b
�����h���[���W�n�͊����n�ɑ��Ĉ�l�������镨�̂���Ƃ�����W�n��
https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%B3%E3%83%89%E3%83%A9%E3%83%BC%E5%BA%A7%E6%A8%99
������Z�̏�������P�b�g���n���ɋA�҂��ׂ�U�^�[���������Ă���ɓK�p����B
���̊����n�� (x, t)�A�Z��̍��W�n��(X, T) �Ƃ���B
�@��� (x,t) �ł̈ʒu�� x = 0 �ň��
�@�Z�� (X, T) �ł̈ʒu�� X = 0 �ň��
�@���P�b�g��U�^�[���������A�n���ɑ��鑬�x�� 0 �ƂȂ鎞�_�� T = t = 0 �Ƃ���
�@U�^�[�������̉����x�� g (��0)
�@T = t = 0 �ɂ����� �n���͌Z���狗�� L ����Ă��� ((x, t) �ł̋����Ƃ��邪 (X, T) �ł������j
�@���̂Ƃ� (x, t) ��(X, T) �̕ϊ��͈ȉ��̂悤�ɂȂ� (���� c = 1 �Ƃ���)
�@�@ t = (X + 1/g)sinh(gT)
�@�@ x = (X + 1/g)cosh(gT) - 1/g - L
�Z����݂���̎��Ԃ��v�Z����ɂ́A�n���̈ʒu x = 0 �ł� t, T �̑Ή����v�Z����Ηǂ�
�@�@
�@�@t / (x + 1/g + L) = sinh(gT) / cosh(gT) = tanh(gT)
�@�@x = 0 �̂Ƃ�
�@�@
t = (L + 1/g)�Etanh(gT)
�@�@dt/dT = (gL + 1) / {cosh(gT)^2}
T = 0 �̂Ƃ��@cosh(gT) = 1 ������AT = 0�ߖT�ł͒�̎��� t �͌Z�̎��� t �� (gL + 1) �{�̑��x�Ői��
���ƂɂȂ�B
��Ƃ��ĉ����x g = 1���N/�N^2 (�� 9.5m/s^2 �Œn���̏d�͉����x�ɋ߂��j�AL = 10���N �Ƃ���� gL + 1 = 11
�ƂȂ�B�����xg, ���� L ���傫���قǐi�݂͑����Ȃ�B �����h���[���W�n�ɂ��킹�ă��P�b�g����Ԃ��߂ɂ͌������������˂Ȃ炸�A�Z�͎��S���Ă��܂��̂œK�p�ł��Ȃ�
������Ȃ�ł�����Ȃł���߂Ȕ��_�͂��蓾�Ȃ����낤�B
>>6�̌v�Z��ł͉����x��9.5m/s^2�ł����Ȃ��B
���������ă����h���[���W�n�̉���}�̂Ƃ������Ƃ�����݂Ă���Ȃ��Ƃ������Ă�̂� ���Ǔ��ꑊ�ΐ����_��>>4�ɓ������Ȃ����Ƃ����_�̌��E�Ȃ��
����ɍX�ɌZ�ɏ��������Ȃ��Ɩ��� �Z���炷������̉��������Ƃ�������
���������ꑊ�ΐ����_�͌Z��������������Ă���Ƃ�������ɗ������o���Ȃ�
>>4
���ꂪ��l�d�͂̂��ƂłȂ�A���O���F�߂��Ƃ���u��l�d�́v�͓K���ȍ��W�����Α�抵���n�ɂȂ�
���̊����n�ł̓{�[���͐Î~���Ă��ČZ�������^�����Ă���B
�����n�Ȃ̂œ��ꑊ�Θ_�Ŗ��Ȃ�������B
���̌��ʂ����̍��W�n�ɕϊ�����ΌZ���猩����̎��ԂɂȂ�B
���̕ϊ��̗��>>6�̌v�Z�ɑ�������B�����h���[���W�n�͂܂��Ɉ�l�ȏd�͏��\�����W�n������ˁB
��l�d�͂łȂ��Ȃ炻��͂����������c��ł���Ă��ƂȂ̂ł��ꂱ�����ꑊ�Θ_�͈̔͊O���B >>5
����J�낻�̐��������ꑊ�ΐ����_�̌��E�Ȃ� >>11
���₾����܂��ɂ��ꂪ���������̓����Ȃ킯��
���ꂪ���ꑊ�ΐ����_�̌��E
�Z��������������Ă��闧��ł����c�_�ł��Ȃ� ���Z�����ł͒�Ԃ̖��ݒ肷����ꑊ�ΐ����_�͂��̗�������Ȃ��@
���Ĉȏ�̂悤��>>4�̐����ɂ͓������������ČZ�̉��������ɕύX���邵���Ȃ�
���������E
�ܘ_��ʑ��ΐ����_�ł͂��̂悤�ȕs�����͂Ȃ��ǂ̗���ł��v�Z�ł����i�q���v��p������̃X�P�[���ł�������I�����\���낤
�܂��ɓ��� > ���₾����܂��ɂ��ꂪ���������̓����Ȃ킯��
������H
���ꑊ�Θ_�ł͏d�͈͂���Ȃ�����Z��̉����n���d�͏�Ɖ��߂��Ȃ����Ă�������B
����͌Z��̉����n�������Ȃ��Ƃ������Ƃ�S���Ӗ����Ȃ��B
> ���ꂪ���ꑊ�ΐ����_�̌��E
���ꑊ�Θ_�Ɂu�d�͈͂����Ȃ��v���Đ���������͓̂�����O�����H
>>15
> ���Ĉȏ�̂悤��>>4�̐����ɂ͓������������ČZ�̉��������ɕύX���邵���Ȃ�
�����u�o�q�̃p���h�N�X���d�̖͂��Ɖ��߂��ĉ����v�v���Ƃ͓��ꑊ�Θ_�ł͖�������B���ꑊ�Θ_�͏d�͂�����Ȃ�����B
�ʂɂ���ȉ��߂����Ȃ��Ă�������̂őS�����Ȃ��B ���Ă��̂悤�ɂ���>>4�͓��ꑊ�ΐ����_�ɓ�����������������ŗ����ς���K�v�����邱�Ƃ��F�߂�ꂽ
���ꂪ���ꑊ�ΐ����_�̌��E�ł���
�Z���炷������̉��������Ȃ̂������ꂪ�o���Ȃ�
���������ɂ���ČZ��������������Ă���Ƃ�������ɂȂ�Ȃ��Ƃ����Ȃ� �u�d�̖͂��Ɖ��߂��Ẳ��ȊO�F�߂Ȃ�����I�v�ƑʁX�����˂Ă邾���B
�������������ďd�͏��������Ȃ��Ƃ����Ȃ����Ǝ��̂��܂��ɓ��ꑊ�ΐ����_�̌��E�������Ă���
���������͓��ꑊ�ΐ����_�̗v���ł͂Ȃ��̂�����
�o�q�̃p���h�b�N�X��>>4���F���K�͂ł����v�l��������>>4�Ȃ猻�݂̉Ȋw�Z�p�ł����ۂɌ��ł������� ��ʑ��Θ_�͓��ꑊ�Θ_�̊g���Ȃ�����ꑊ�Θ_�Ɂi��ʂɔ䂵�āj���E������͓̂�����O
���̌��E�������Ă��o�q�̃p���h�N�X�̌Z���_���l����̂Ɏx��͂Ȃ��B
�����������g���ΌZ��̉����n���d�͏�Ɖ��߂��邱�Ƃ��ł��邪�A����͑o�q�̃p���h�N�X�ɕK�{�ł͂Ȃ��B
�����āu���ꑊ�Θ_�Ŕ��n���������Ƃ���Ɛ����閵���v�Ƃ��͌��Lj�؎�����Ȃ������B
�Z��̍��W�n�Ȃl�����Ƃ���ŁA�V����������m���͉��������B
>>23
>�V����������m���͉��������B
�o�J�]�̌��E >�����������g���ΌZ��̉����n���d�͏�Ɖ��߂��邱�Ƃ��ł���
���ꂪ����ւ��Ȃ��
>>11������Ă���̂͏d�͂������ɂ���ď����Ă���킯��
>>4�ɑ��ē��ꑊ�ΐ����_�ł͂Ȃ������������g���Ă� ���ꑊ�ΐ����_�Ő����ł���Ȃ瓙���������g�킸��>>4���������悩�����̂������ǖ����������킯�� >>25
���Ƃ��Ƒo�q�̃p���h�N�X�̐ݒ��
�E��͊����n�ŐÎ~���Ă���
�E�Z�͂��̊����n�Ō��ĉ����^������
���̖���
�@��l�ȏd�͏�̂Ȃ��ŌZ���Î~���Ă��āA��i�ɑ�������{�[���j�������ɓ����Ď��R����������
���ɉ��ς����̂͂��O������ɂ���Ă邱�Ƃ���B
�Z�̉����^���̂���U�^�[���̕����������Ƃ��āA����l�����Ɍ��肷��ΌZ��̍��W�n����l�ȏd�͏�ƌ��Ȃ��邩��A���̉��ώ��̂�
�����Ƃ͌���Ȃ����A����͓��ꑊ�Θ_�͈̔͂���E���Ă�B
���x�������悤�ɓ��ꑊ�ΐ����_�͏d�͂������Ȃ�����d�̖͂��ɉ��ς�������ꑊ�ΐ����_�ň����Ȃ��͓̂�����O�B
�����ǖ{���̑o�q�̃p���h�b�N�X�������̂͂Ȃ�̖����Ȃ��B
���O�́u�d�̖͂��Ƃ��ĉ����Ȃ���t��F�߂Ȃ��v�ƑʁX�����˂Ă邾���B >>27
���̐ݒ�̑o�q�̃p���h�b�N�X�͒n�����Z�̌����o�Ė߂��ė�����
��������͎v�l�����ł��܂�ɂ������Ƃ������ꂽ�K�͂Ȃ̂Őg�߂ȃ{�[�������ɒu������������
�o�q�̃p���h�b�N�X�̖{���͒n����U�^�[���̉����ɂ���̂ł��̕����������o������
�������������ɕ�����Ă��邱�Ƃ͖{���I�ł͂Ȃ�
�n�����Z�̌�������-g�Ō������Ă��Ė߂��Ă������̎��v���ׂ邾�� �o�q�̃p���h�b�N�X�͍��Ȃ��K�͂��傫�߂��ĕ�����ɂ����̂ʼnE�ɒ���������
��Ԃ̐ݒ�ł͓������Ԃ�p�ӂ��Ă邪����̓p���h�b�N�X�̖{���ł͂Ȃ��̂ŏ��߂��炱��ł���

���ꑊ�Θ_�ł����n�ŋL�q���邱�Ƃ͖��Ȃ�
������ʑ��Θ_���Ƃ����Ȃ���W�n�ł��������������ł��邪�A
����ł͂���͖�������Ȃ�(���R�v�ʂɂ�������̂�������ɓ�������Ή\����)
>>29
����͑o�q�̃o���h�b�N�X�ł͂Ȃ��B �ǂ̖{�ɂ����o�q�̃p���h�b�N�X���Ɛ������Ă�����̂�����Ƃ����̂��H
���O������Ɍ����Ă��邾�����B
>>30
> ������ʑ��Θ_���Ƃ����Ȃ���W�n�ł��������������ł��邪�A
�����>>28�݂����Ɂu��ʑ��Θ_�ł͊����n�Ɣ��n�̋�ʂ��Ȃ��v�Ƃ������o�L�ڂȗ������Ă������ˁB >���ꑊ�Θ_�ł����n�ŋL�q���邱�Ƃ͖��Ȃ�
������āA�����h���[���W�n���]���W�n�Ȃǂ͓��ꑊ�Θ_�̔��e���Ƃ����Ӗ����H
���R�Ȏ���ɂ����ē��ꑊ�Θ_�Ŕ��n���L�q���邱�Ƃ��莋�����́A
���ʂɋɍ��W�������Ă���̂����āA���W�����Ȃ����Ă��邩�烆�[�N���b�h�̔��e�O�A
�Ƃ������}�k�P�Ɠ������ȁB
�n���̂ق������o�q�̃p���h�b�N�X�Ȃ�Ďa�V����
>>34
�����A�v�ʂ��t���b�g�Ȃ��Ƃ����ꑊ�Θ_�̕K�v�\�������Ȃ̂�
�������A�Ⴆ�Ή�]�n�Ŕ��a������l���傫���Ȃ�Ƒ��x����������
�����ł͌�������̓��ٓ_������āA���W�n�ɂ����E�������邱�Ƃɒ���
����͈�ʑ��Θ_�̃u���b�N�z�[�����ł��悭���邱�� >>38
���ꑊ�Θ_�̕K�v�\������������ł��邱�Ƃɂ͈٘_�����邪�A�Ƃ肠�������������B �h�f�l�ł����A��ʂ�����̕����ʔ����������܂�
��ʂ͎��ό`�̉J�����ŐS�܂�܂�
>>31
�o�q�̃p���h�b�N�X����
�n�����o�Ă����Ƃ��������ے�ł��Ȃ������
���ꑊ�ΐ����_��>>4������ł��Ȃ��̂œ������������p���ďd�͂������Đ������邵���Ȃ��̂��i>>11�j >>37
�a�V�������Z���炷������Ȃ̂�����d���Ȃ�
�n���Ƃ����v�l�����ł͋K�͂��ł��߂��Ĉَ��Ɏv���邪�Z���{�[���̉����������ϑ������Ƃ��{�[���������Ă邱�Ƃ�������a�V���H
���̎��͔J��Z��������������Ă���Ƃ�������̂ق����a�V���낤��
���ǂ���͓���I�Ȓ����Ƃ̃Y���ł����Ȃ� >>41
�o�q�̃p���h�b�N�X���ƌ��������Ȃ�A���̃\�[�X���o����B���O�̍l���͗v��Ȃ��B >>43
> �a�V�������Z���炷������Ȃ̂�����d���Ȃ�
�킪�����n�ŐÎ~���ĂČZ�͂��̊����n�ɂ����ĉ����^������A�����̂��������̐ݒ�ŁA
���̏�Łu�Z����݂�Β�̂ق�����������v���Ă����̂��ƁB
��������ɖ߂��Ί����n�ɂȂ�͓̂�����O�B���������ȂǑS���s�v�B >>44
���ɏ�Ő������Ă���
�N���Z���̒킾�̂ɍS��l�Ȃ�b�ɂȂ�Ȃ��̂Ō��\����
�����ł͐l�͏d�v�ł͂Ȃ����v�ł�������̂� >>45
�Z���炷��Βn���̔��˂ł����Ȃ��킯����
�����Ă����U�^�[�����Ă��邾����>>29�̂悤�ɂ�
�Z�ɂƂ��Ă̓{�[���𓊂��ĕԂ��Ă������̎��v�̃Y���ׂ邾��
���O�͓��������ł������������킯��>>11
�ܘ_���������ɂ��d�͏����͐�����
����͈�ʑ��ΐ����_�̓����� �悤�킩��njZ���E���̌ŗL���Ԃƒ퐢�E���̌ŗL���Ԃ��r������������ł́H
>>46
���v���낤�Ɛl�Ԃ��낤�Ɠ�������B
���O�̐ݒ�͏��Ȃ��Ƃ���ʂɁu�o�q�̃p���h�N�X�v�ƌ�������̂ł͂Ȃ��B >>48
�ĉ�̔N����r�����������Ȃ炻��ŏI���B
�Z�A�킻�ꂼ��ɂƂ��Ă̑���̎��Ԍo�߂���ɂ���Ȃ炻�ꂾ���ł͕s�\�� >>46
�����͕s�v���B�\�[�X���o���B >>47
�{��j�ɐl�̘b���Ȃ�����ȁB
> �Z���炷��Βn���̔��˂ł����Ȃ��킯����
�u�Z���猩��Βn�����������Ă�v��ے肵�Ă��͂��Ȃ��B >>49
�o�q�̃p���h�b�N�X�ɂ͌Z�i���v1�j�ƒ�i���v2�j�������
�����ČZ����̉����������ϑ����Ď����̃Y���ׂ邾��
�n�����Ɖ�����������邱�Ƃ͓���I�Ȓ����łَ͈���������͖O���܂Ŋ��o�̘b�ł����Ȃ� ���njZ���_�ł�>>4�̃��f���Ɠ����Ȃ�
�n����-g�Ŗ߂��Ă���̂��m�F���邾�� >>53
> >>49
> �o�q�̃p���h�b�N�X�ɂ͌Z�i���v1�j�ƒ�i���v2�j�������
> �����ČZ����̉����������ϑ����Ď����̃Y���ׂ邾��
> �n�����Ɖ�����������邱�Ƃ͓���I�Ȓ����łَ͈���������͖O���܂Ŋ��o�̘b�ł����Ȃ�
����͉��ɑ��Ĕ��_���Ă�킯�H
��̎��v�����邱�Ƃ�ے肵�Ă�����H
�Z���猩����̎��Ԃ����ł��邱�Ƃ����ꂩ�ے肵���H �\�[�X���o���Ƃ����v���ɂ͖������B
�ǂ�������������Ύ����ɑo�q�̃o���h�b�N�X�̓��e�����߂錠��������ȂǂƎv����̂��B
>>56
���_���������ꂪ�S�Ă���
���v�͂������Ԃ����ނ����Ȃ̂Ŗ߂��Ă����Ƃ��Ɍ���ׂ邾����
�����Ď��v1,2�̃Y�����ǂ��Ȃ��Ă��邩
�o�q�̃p���h�b�N�X�Ō�����݂��ɒx��Ă�Ȃ�Ă��Ƃ��N���Ȃ��̂͂���ŕ����邱�� �����Ă��̃��f���Ƃ���>>4���������������̂���
�������͂��O�̂悤�ɓ���������p���ďd�͏������Ă��������������Ȃ����@�ł��悢
���͂⍡�̎��セ���œ���ꂽ���ʂ͒n������ł�����؉\���x���̖��ɂȂ� >>58
> ���v�͂������Ԃ����ނ����Ȃ̂Ŗ߂��Ă����Ƃ��Ɍ���ׂ邾����
> �o�q�̃p���h�b�N�X�Ō�����݂��ɒx��Ă�Ȃ�Ă��Ƃ��N���Ȃ��̂͂���ŕ����邱��
�߂��Ă������_�ł̎��v�̎w�����������W�n�ŕς�邱�Ƃ͂Ȃ����炻��Ȃ��Ƃ͂͂��߂���킩�肫�������Ƃ��B
�r���o�߂���Ȃ��Ȃ瓙��������������ؕK�v�Ȃ��B �o�q�̃o���h�b�N�X�Ŏ��v���݂��ɒx���ƌ�����̂́A
���҂��Î~�܂��͓����^�������Ă���Ƃ����O���邩��Ȃ̂ɁA
���̑O���ے肵�Ă��܂�����A�����Ă��邱�Ƃ����Ӗ�����ȁB
>>50
�ǂ��������ƁH���ꂼ��̌n�ɂ����邻�ꂼ��̃C�x���g�̎������Ă��ƁH �����n (x, t) �ł̌ŗL���т�
�@d�� = ��(1-v^2) dt
�̐ϕ��ŕ\������ˁB�o��������ĉ�܂ł̒�A�Z�̂��ꂼ��̐��E���ɂ����Ă��̐ϕ��������
�ĉ�̗��҂̌ŗL���͋��܂�B�ĉ�̎��v�̔�r�����邾���Ȃ炻��Řb�͏I���B
�ǂ��������W�n�������Ă��悤���ŗL���͕ς��Ȃ�����ˁB
�r���o�߁A�܂�
��̌ŗL������1�̂Ƃ��Ɂi���ł́j�Z�̌ŗL��
�Z�̌ŗL������1�̂Ƃ��Ɂi�Z��ł́j��̌ŗL��
��m�肽����ΌZ��̐��E���̊ԂɑΉ��t�����K�v�ɂȂ�B
�@�@
���ꂽ�n�_�ł̎����̔�r�͖{���I�ȈӖ��͂Ȃ����炠�܂�C�ɂ��Ȃ������c�_���X�b�L������
�ŏI�I�ɔ�r�ł��鎞�v�̎����͎���̓��n�_�ɂ�����̓��m������
>>60
���_�Ƃ��̎����I���͕ʕ���
>>4��������p���ďd�͏������邩�d�͂ڈ������͎��R��
�ǂ���ɂ��낻�̌��ʂ͌��i�q���v��p���ăY�����ϑ����ė\���ƈ�v���邱�Ƃ��m�F����悢 >>64
��������ˁA��ʑ��Θ_�ł͍��W�n�̎����ɂ���đ���̎����Ȃ�Ăǂ��ɂł��Ȃ邩��r���Ŕ�r���Ă����Ӗ��Ǝv���B
���ꑊ�Θ_�Ȃ�Z���猩����̎������킩�猩���Z�̎�������ӂɌ��܂�ł��傤���ǁA�{������ɂ���܂�Ӗ��͂Ȃ����ƁB >>61
���v�̒x��͓����^���ł���K�v�͂Ȃ� >>64
���̒ʂ�
������{�[�����߂��Ă������Ɏ��v���r����K�v������
�����łȂ���Έ���I�ȓ����x�^���������l���邾��
�����Ńp���h�b�N�X�I�Ȃ��Ƃ������Ă�����͖��ɂȂ�Ȃ� �������S���̈ӌ�����v���܂����ȁB
����ł߂ł����߂ł�������ˁH
>>69
�����^���łȂ���Ύ����͐Î~���Ă���Ǝ咣�ł��Ȃ��B ���Ȃ݂Ɏ����I�F�����l���ē����^���ōĉ��P�[�X���l������
��ʑ��ΐ����_�ł͂����������E�����̉F���͋������̂�
>>73
FLRW�v�ʂ�O��Ƃ���Ȃ玞�Ԑ����̌W���͂P��������ꑊ�ΐ����_�Ɠ��l��
�قȂ�ꏊ�ł��݂��ɐÎ~���Ă��瓯�����p���I�ɒ�`�ł���� �܂��A�����w���Ă̂͌��ۂ�m�邱�Ƃ���ŁA�����\�������Ȃ�ē�̎��B�@�W����[���m�肽���Ȃ琔�����w�ׂ�낵�B
���ۂ�m�����i�K�ŁA���̐��E������Č�����͂����B����ŗǂ��B
>>75
��������
�����w�̕��ł��ĂȂ������ɐ����A�Ă���z����ꖼ >>76�m���Ă邩�̗l�ɁA�J�b�R���邶���B
�����͓�̎������A�������ߒ���1�̎����炢�̏��ɂ���ȁB�N�̎����Ă�m���ŁAe=mc^2�̎Z�o�ߒ������߂��Ă���
����ȃV���v���Ȏ��Ȃ���A�����Ɨ]�T����B ����ȂƂ���ŃN�\�݂����ȌȂ̉��l�ό��͕s�v���
�������萔�w�I�ɒǂ���������{����H
�Ȃ������Ă���
���������Ǝ��ʂ������A�����x�ł͎��ʂ�������ɂȂ���
���������葁���҂͑��݂��Ȃ��B
����ł����Ă���
���������Ď��ʖ����傩
�����т܂����Ă��S�R�d���Ȃ��B
�������������q�̎��ʂ����Ȃ�
���Ă��Ƃ͌����x�ł����ʂ͕ς�炸�A
�������͑��݂������Ȃ��̂��H
���ʖ�����Ƃ����̂Əd��������Ƃ����̂��Ⴄ�̂�
���n�ł����ς�킩��Ȃ�
>>80
>���������Ǝ��ʂ������A�����x�ł͎��ʂ�������ɂȂ���
����͑O����I�ȍl����
���͎��ʂ͕s�ςƍl���� ����ł̓��ꑊ�ΐ����_�ł́u�Î~���ʂ��ۑ������v�ƕ\������B
�A�C���V���^�C���̎���ł́A�j���[�g���͊w�� ma=F ����{�I�ƍl���Ă���
����ނ͂��̌`���Ř_�����������B
�Î~�����n����ϑ����Ĉ��͂ʼn����x�������ɋ߂Â��ƌ������郍�[�����c�ϊ�
�����ʂ̑����Ƃ��ĕ������߂����B
���̉��߂ł͐ڐ������Ɩ@�������̎��ʑ������قȂ�Ƃ����s���R�ȕ\���ɂȂ�B
�����w�͐��w�ƈ���ĕ������߂��K�v�s���ł���A�������߂��炻�̎���̊T�O��
�����ł���B
���㕨���w�ł̓��[�����c�ϊ�����{�I�ȕ����T�O�ł���
�t�ɃK�����C�E�j���[�g���̍��W�ϊ��͓���ȋɌ��ƂȂ�B
>>82
�Ȃ爟���������݂������� >>86
������܂�����B
�������̈Ӗ����������ĂȂ��낤���A����ȏ�Ԃł悭�������ނ�B �r�n�Ƃr�L�n�̈Ⴂ���ŏ������ł��Ȃ��������ǁA(���C������)�V�������r�n�A�ʉ߉w���r�L�n�ƍl���������悤�ɂȂ����}�l�ł�
(�u�ŗL���ԂƂ͎��v���Î~���Ă��銵���n�ő����鎞�ԁv�Ƃ����L�q���A���v���~�܂��Ă��玞�Ԍv��˂������Ƃ�)
🚄���C���V�����������ʂɌ������Ď���300km/h�ő����Ă鎞�ɐV�������猩�Ēʉ߉w��x������300km/h�ʼn߂��čs���Ȃ���
�ʉ߉w�̎��v�͊m���ɂr�L�n�ŐÎ~���Ă�Ȃ�
�܂�����300km/h�Ȃ�ĕb��80m/s���x�����ǂ�
>>88
���ʂɃK�����C�ϊ����킩���ėǂ������� >>87
������葁�����̂����݂������� ��������
�q�ǂ��Ȋw�d�b���k�ŕ���
Calc Letter�Ƃ����\�t�g���g���ē������x�^���̃O���t��`���Ă݂��B
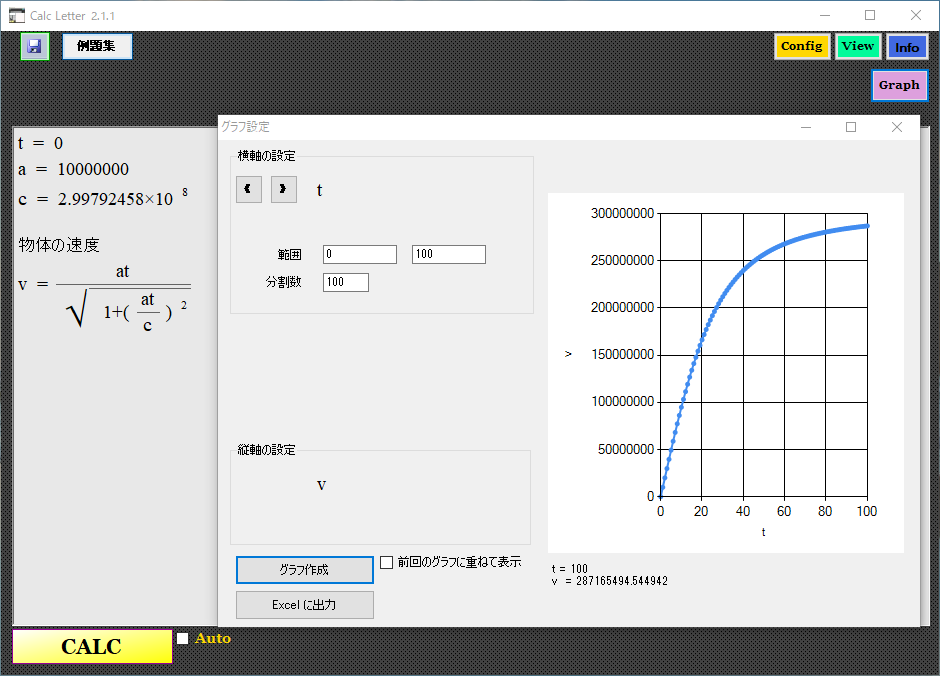
�����������Ă������x�͒������Ȃ��͗l�B �������������x�^�����Ă��镨�̂̌ŗL���Ԃ��o���Ă݂邽�B
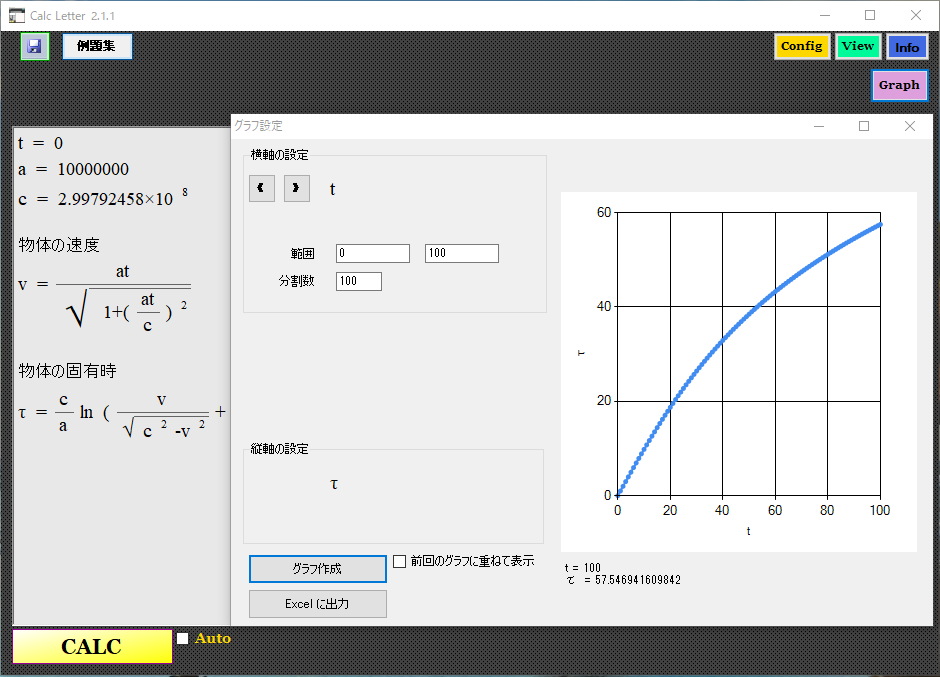
���Ԃ̐i�ݕ�������������ɂȂ��Ă����̂��킩��B �t�ɕ��̂���n���̎���t'������ƁA�n���̎��Ԃ̕�������������ɂȂ��Ă����B
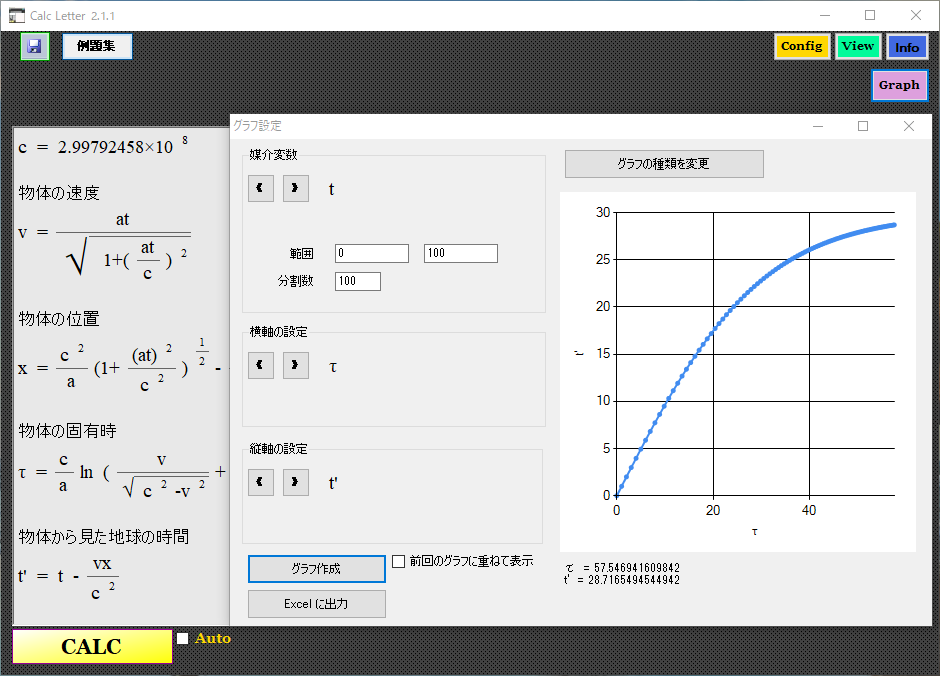
���̂��猩���n���̈ʒu�B
�ŏ��͉������Ȃ������ɗ����čs���Ă邪�A25�b�߂��������肩�猸���ɓ]���Ă�B
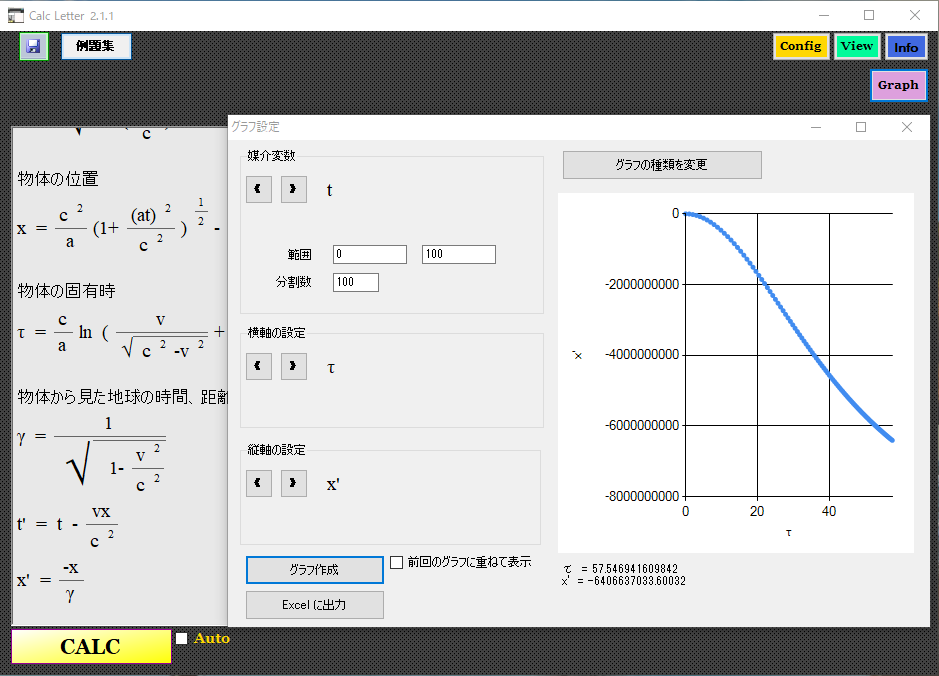
�ŏI�I�ɂ͂قƂ�Ǔ����Ȃ��Ȃ��Ă���B
���̂����肪�������x�^���ɂ����鎖�ۂ̒n���ʁi�����h���[�n���ʁj
���Ȃ݂ɂ����܂ň�ʑ��Θ_�͎g���Ă��炸�A�S�����ꑊ�Θ_�ň�����b�ȁB
>>92-95
a=9.8m/s^2�Ōv�Z�������������������Ă��炦��Ǝv�����B ���₢����ꑊ�ΐ����_�Ŕ��n�͈����Ȃ��Ƃ����l���������炻�̘b�肾��
��������ăO���t�Ŏ��o�I�Ɏ����Ă����̂͂��肪����
���Θ_�̃e�L�X�g�ɍڂ��Ă鎮�ŃO���t�`��������������Ȃ�
���܂��炢���O���t�ꔭ�ł킩�邱�Ƃɂ��ĉ��X�s�тɋc�_���Ă邾��
>>80
���̎��ʂ�0
���͐Î~�ł��Ȃ�����Î~���ʂ͂Ȃ����A���q�̃G�l���M�[�^���ʂ�
E^2-p^2=m^2
����(���[�����c�s�ϐ����E�ӂ͕K���萔�ɂȂ�)
���̎���m=0�̎����g���A���ꂪ���L���Ӗ��Ŏ��ʂ̒�`�Ƃ���Ă��� >>99
���������l���ė��_�̘_���\���Ƃ����T�O���Ȃ��낤�Ȃ� �j���[�g���͊w�ŃV���o���c�V���g���a�o�ł���Ǝv���Ă�l�����邩���
���_�\����茋�ʂ��S�ĂȂ̂�
>>99
�Ђ���Ƃ��ĉ��̂��Ƃ��H
�����Ă������A���̎咣�́u�����Ȃ��v�ł͂Ȃ��u����Ȃ��v���B
�P�ɓ��ꑊ�Θ_���ǂ����̐������̘b�ł����āA
����Ȃ̂͐l�ɂ���Č���������Ă��Ă����̖��������͂����낤�B >>105
�u������v���Ƃ�F�߂�̂��H >>105
���͈���Ȃ����Ď咣���Ă�́H
�l�I�Ȏ�`�ɂ��Ă͂ǂ��������R�ɂƂ��� >>109
�����B���݂������R�ɁA���B
��`�̉������͎~�߂Ă����B >>111
�������l�I�Ȏ�`�͍\��A���ꂾ�Ƃ����̘b��ɂ��ĉ�b�ł��Ȃ����ƂɂȂ�B
�킴�킴���͉�b�ł��Ȃ��錾���ɂ��Ȃ��Ă��������ŁB
�X���̍ŏ��̕��Łu���Ǔ��ꑊ�ΐ����_�̌��E�v�Ƃ������Ă��̂͂Ȃ����낤�ȁH �Ⴆ�ΊȌ��ȃ��f��>>4��說���ł��Ȃ����Ƃ͓��ꑊ�ΐ����_�̌��E�Ǝw�E�����͉̂�����>>105=>>34�Ƃ͕ʐl������
�ŏI������b�Ȃ̂ɏ�������u���Ă���Ԃ�Ԃ��Ă����͉̂��̂Ȃ낤�cw >>113
���� = �u���͔��n�̓��ꑊ�ΐ����_������Ȃ��v�Ƃ����l�I�Ȏ�`
>>114
�Ԃ�Ԃ����Ȃɂ��A���̃X�������������ł����ȁB
���ɔ��n���猩���n���̈ʒu�⎞�ԂȂ�āA���ꑊ�Θ_���瓱�o�����O���t�łȂ�ڂł���������Ă��ł��傤�B >>115
���₻����Ă̂�
>�X���̍ŏ��̕��Łu���Ǔ��ꑊ�ΐ����_�̌��E�v�Ƃ������Ă��̂͂Ȃ����낤�ȁH
�̃��X�̘b��
���Ǖʐl�������� >>115
�����܂ő��Θ_�̈�ł����Ȃ�����Ȃ�
���̃X���̓X���^�C�ʂ葊�Θ_�S�Ă��܂��Ă�̂�
�����Č�����ID:Sfw8+M9z���������߂闧��ɂ��邪
�����Č���>>4�͓����������g�����ؖ���������Ȃ������̂ł����Řb�͏I�������� �܂��ނ̔����𒍎߂���Ȃ�u�i���ꑊ�ΐ����_�Ɋ܂܂�Ȃ����������ŏd�͂���������j���ꑊ�ΐ����_�Ő����ł���v���Ă��ƂȂ낤
�����Ă���͒N���ے肵�ĂȂ�
>>117
>>4�͌��lj����^�₩�{�l�ȊO�N���킩���Ώ��ł��Ȃ������̘b��ŁB
�����h���[���W���O���t�ł����Ȑl���������ĂĂ��s���Ƃ��ĂȂ��݂��������A���lj����^�₩�͂킩�炩�����܂��B
���_�Ƃ��Ă͔��n�����ꑊ�ΐ����_�ň�������Ęb�ɂȂ��Ă�B�i�l�I�Ȏ�`�̂��߈���Ȃ����Đl�̂��Ƃ͒u���Ƃ��āj ���Ȃ݂ɒn��̂悤�Ȑ^�̏d�͏�͓��ꑊ�Θ_�ł͈����Ȃ��Ƃ����b�������Ȃ�������͂�����܂��B
���Ƃ͑o�q�̃p���h�b�N�X�̐܂�Ԃ��Ŕ������鉼�z�I�ȏd��(������)�̘b�������Ǝv�����A������͓��ꑊ�Θ_�̔��e�B
>>119
���⏭�Ȃ��Ƃ��u3�v���Đl�͗������Ă���>>11�̂悤�ɓ���������p���ďd�͏������邱�Ƃœ��ꑊ�ΐ����_�ɂ��������ʂ�������
�����Ă���ȏ�͂Ȃ������̂ł����ŏI����Ă�b
�u3�v�����ɂȂ��ĂԂ�Ԃ��킯�ł�����܂����ˁH�c >>121
�ǂ��������ĂR�����݂̐^�ӂ����炸�������Ȃ������ȂƒT��T�����Ă�悤�Ɍ����邪�H �J����؉Ȋw�Ƃ�������ł͏d�͂̉e���������Ǝ�荞�v�Z�i���i�q���v�Ŏ����I�ɂ����o�\�j�Ɠ��������ŏd�͏������ē��ꑊ�ΐ����_�Ōv�Z�������ʂ���v���邱�Ƃœ��������̐������̍����̈�ɂȂ邾�낤
�܂�����ȊO�ɂ���������̎����͊��ɍs���Ă���̂ł��̐������͍��X�^���܂ł��Ȃ��킯����
>>122
����>>11�ł����Ɠ��������ɂ��d�͏����𗝉����Ă����
�����Ă���������ł͓��ꑊ�ΐ����_�Ő����ł���Ƃ܂Ō����Ă���
�܂��ɉ��̌����Ă��邱�ƂƓ����ł����ŏI������b
�u�i���ꑊ�ΐ����_�Ɋ܂܂�Ȃ����������ŏd�͂���������j���ꑊ�ΐ����_�Ő����ł���v������ >>121
�n��̘b�Ȃ��l�d�͂ł͂Ȃ����A�o�q�̃p���h�b�N�X�̐܂�Ԃ��̘b�Ȃ炻�������d�͂ł��Ȃ����A
����������ďd�͂ƌĂԂȂ�Γ��������őł��������炢����˂��Ęb���낤�B
���ǂ��݂̐^�ӂ͂킩�炸���܂������A����Ŕ[���ł����Ȃ炻��ł�����˂��Ęb���Ǝv���B >>124
�����͂���d�͂Ƃ݂Ȃ��Ƃ����ςȒ�`������Ȃ�A���̏d�͓͂��������őł��������Ƃ����b���낤�B
�{���͑o�q�̃p���h�b�N�X�̐܂�Ԃ��Ŕ�������͂͏d�͂ł͂Ȃ��̂œ��������ȂǏo�開���Ȃ��B
�ł����������݂��������Ǝv���ĂĂȂɂ����������̂��͕s���Ȃ܂܁B >>125
���ԂO�͂��Ă���ĂȂ�
�n��ł̏d�͂͌����ɂ͈�l�d�͂ł͂Ȃ��I���Ă̂͋c�_�Ƃ��ăY���Ă���
�u3�v�͂��̕ӂ̗����͓��R���Ă����̂ł����������I�O��ȋc�_�͋N���Ȃ�������
���Ɂu3�v�Ƃ����c�_�̑O������X�c�_���Ă��Ӗ��Ȃ�����
���P�b�g���l���鎞�����Ēn���̏d�͂Ɋւ��ċߎ����邵��
�܂��m���ɂ��̕ӂ̊��o���āu3�v�ɂ͒ʗp���Ă������ő��̐l�ɂ͓���̂�������� >>126
��l�d�͓͂K���ȍ��W�ϊ��ő��I�ɏ����ł���Ƃ����b�ł���͊���>>11�ł���Ă邩���
�����牴�̖��͌�����>>11���������Ă�킯�� >>127
���₫�݂����Ă���ĂȂ����A�R�̈Ӑ}�����Ⴂ���Ă�̂�
�R�͑��d�͂łȂ���Αł������Ȃ����Č����Ă�ł��傤�B
�܂�n��̏d�͂͑��I�ɑł������Ȃ��B�܂���ꑊ�Θ_�ł͐����ł��Ȃ��b�B
�o�q�̃p���h�b�N�X�̐܂�Ԃ��͏d�͂łȂ����A���݂��ǂ����Ă��Ƃ����Ȃ�d�͂Ƃ݂Ȃ��ē��������őł������Ă������B
�킴�킴����Ȃ��Ƃ�����Ӗ��͂Ȃ����A�ǂ���ł����ꑊ�Θ_�Ő����ł���Ƃ������_�ɂ͕ς��Ȃ��B �������Ƃ��Ă�>>11�������ɐ������Ă��ꂽ�̂ł����ŋc�_�Ƃ��Ă͏I���Ȃ��
��l�d�͂������ɂ���ď������đ�抵���n�����
�����ł͓��ꑊ�ΐ����_�Ŗ��Ȃ�������
�܂��Ɂu�i���ꑊ�ΐ����_�Ɋ܂܂�Ȃ����������ŏd�͂���������j���ꑊ�ΐ����_�Ő����ł���v���� >>129
����u3�v�͂��̉����������f������l�d�͏ꒆ�ł̘b���Ɨ������Ă�����
�n��͌����ɂ͈�l�d�͂ł͂Ȃ��I�Ƃ����N�ɂ͋c�_�̑O���L����Ă��Ȃ��̂ł��Ă���ĂȂ��悤������
�����܂Ŏv�l�����ɂ�郂�f�����������
�����牴���n���ƃ��P�b�g�̃��f���ɑ��Č����ɂ͒n���̏d�͂��邩��v�Z�ɂ͈�ʑ��ΐ����_���K�{���I�Ȃ�ēI�O��Ȃ��ƌ���Ȃ�
���̕ӂ̊��o�́u3�v�Ƌ��L����Ă����悤�Ŗ��͋N���Ȃ������Ȃ� >>130
�����ƌ����Ă邪�A�܂�Ԃ��Ŕ�������͂͏d�͂ƌĂȂ��B
�o�q�̃p���h�b�N�X�͓����������Ȃɂ��v�炸�A�A���ׂē��ꑊ�Θ_�݂̂Ő����ł��Ă���B
�܂�Ԃ��o������͂����݂��d�͂ƌĂԂ��瓙�������Ȃǂ�₱�����b����������Ȃ������B
���݂͂���킩���ĂȂ��݂��������A�R�������Ă���̂͂��������Ë��_�̘b�B
�ǂ����Ă����ĂR�͈�т��Ă��݂ɔ��_���闧�������Ă��ł��傤�B ���Ȃ݂Ɍ��ݍł������x�̎��v�̈�ł�����i�q���v�ł���n��ł̏d�̓|�e���V�������͇�h�Ő}����
�����Đ܂�Ԃ��n�_�œ��������͂ƁA�n��̂悤�ȏd�͍͂����ł��Ȃ��Ƃ��������������Ă���B
�O�҂͓��ꑊ�Θ_�Ő����ł��邪�A��҂͈�ʑ��Θ_���B
�ǂ���̘b���������B
>>132
���m�ɂ͌ĂȂ����߂ɓ���������p������
�J��Ԃ��ɂȂ邯�ǂ�����Č���>>11�̂���Ă邱�ƂƓ����Ȃ̂� ���̗L���ȃX�J�C�c���[�ł̌��i�q���v�����������Ⴞ
�������ĂA�d�͂ƌĂȂ��Ȃ�A�����������g���
�d�͂ł͂Ȃ����瓙���������g���K�v�͂Ȃ��B
���lj��̌����Ă�w�ǂ�>>11�Ő�������Ă���
�ꕔ�̐l�ɂ͍Ō�̈�l�d�͂ł͂Ȃ��Ȃ�`�̕����������|�����炵��
���������Ɓu3�v�̊Ԃł͉����������f���͈�l�d�͏ꒆ�Ƌ��L����Ă����̂Ŗ��Ȃ�����
�����ɂ͒n��ł͈�l�d�͂ł͂Ȃ����Ă̂͊O��̋��L�s���ɂ��F���̃Y��
�݂��Ɏv�l�����ɂ����郂�f�����𗝉����Ă���̂ʼn����I���W�i���ł̒n���̏d�͂Ȃ�Ė��Ȏ�����Ȃ�
����͑��ΐ����_�̖��Ƃ�����蕨���w�ɂ�������@�_�̖�� �����]�X�����Ȃ��̗��ꂷ����I�ɏd�͂������Ȃ��̂œ��ꑊ�ΐ����_�ɋA�������Ē�ʌv�Z�ł��Ȃ������
�܂����͂���Ȗ��Ȏ������������w�̕��@�_�ɂ��Ė��m�Ȃ킯�ł͂Ȃ��̂�
�����v�l�����Ƃ������̂��ĊO�Ȋw�ɋ����Ȃ��l�ɂ͓���T�O�Ȃ̂��������
>>138
>>11�͑o�q�̃p���h�b�N�X�̐܂�Ԃ��͓��ꑊ�Θ_�I�����[�Ő����\���Č��_�ɂ����Ȃ��Ǝv�����B
�{�������œ����͂��d�͂Ƃ݂Ȃ��K�v���Ȃ���ᓙ���������g���K�v���Ȃ��̂͂��݂��킩�����Ǝv���B
���̏�ł��݂������������������������Ƃ��ĉ����ˁH
�u�܂�Ԃ��n�_�œ��������͂��d�͂Ƃ݂Ȃ��̂����肾���A������������g���đł������̂����肾�낤�v���Ęb�ō����Ă�H ���肩������A����łȂɂ��������˂�Ƃ��������悤���Ȃ����
�ق�܉����킩���Ăق�����������B���̂Ȃ��咣������
>>11�̌����Ă���悤�Ɉ�l�d�͓͂K���ȍ��W�ϊ��ő��I�ɏ����đ��I�����n������i���������j
�����Ă��̌�͓��ꑊ�ΐ����_��p���čD���Ȃ悤�ɋc�_���邱�Ƃł��ł���
�܂��ɉ��������Ă��邱�Ƃ����
�d�͂������͂Ƃ��Č������ꍇ������ł���
�Œn��͌����ɂ͈�l�d�͂łȂ��Ƃ����w�E�͑��ΐ����_�̗����̍��ł͂Ȃ��v�l�����̃��f�����Ƃ��������w�̕��@�_�ɂ��Ă̗����̍�
���������y�͂��������I���W�i���̃��P�b�g�ƒn�����f���̒�̗��ꂷ����ꑊ�ΐ����_�Œ�ʌv�Z�o���Ȃ� ���Ȃ݂Ɂu3�v�͎v�l�����Ƃ������@�_�𗝉����Ă����̂�>>11�̂悤�ɉ��Ă���
�����ȏ����ΐ����_�̗����̑O�Ɏv�l�����Ƃ������@�_�𗝉����邱�Ƃ̕����悾�Ǝv������ >>142
�n��͌����ɂ͈�l�d�͂łȂ��Ƃ����w�E�͂��݂̈Ӑ}���������������������B
���ꑊ�Θ_�̘b���������̂��A��ʑ��Θ_�̘b���������̂��B
�ǂ������݂͑�抵���n������ꍇ�̘b�����Ă���悤�Ȃ̂œ��ꑊ�Θ_�̘b���Ƃ����̂͂킩�����B
���݂������Ă�̂͊ԈႢ�Ȃ����ꑊ�Θ_�I�����[�ň�����b�ł����Ȃ��B
�d�͂Ƃ������t�͂���Ȃ��ł悢�����������Ƃ������t���s�v���B
���ꑊ�Θ_�̘b�����Ȃ���d�͂��̓����������̌����Ă邩��F����������B
�d�͂ł͂Ȃ������͂ƌ��������Ă������ׂĉ������B >>144
�v�l�����Ƃ������@�_�ɂ���Ēn��ň�l�d�͉��ł̉����������l����킯��
>>11�Ō����Ă���悤�Ɉ�l�d�͓͂��������ɂ���ď������đ��I�Ɋ����n����邱�Ƃ��ł���
�����Ă��̌�͓��ꑊ�ΐ����_�ŋc�_���Ă悢
���I�����n������d�͏�͓��������ɂ���ďd�͏����������Ă��܂��Γ��ꑊ�ΐ����_�̔��e�Ƃ�����������
��͍D���ɍ��W�ϊ������炢�� >>145
�v�l�����Ƃ��≽�ł����肿�Ⴄ���B
���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��B
���Ƃ��Ƃ����ꑊ�ΐ����_�̔��e���Ă��ƁB
�ݒ��Ȃ����̂��Ȃ�������肠��Ɖ��肵����ŁA�ł������Γ��ꑊ�ΐ����_�����藧�ȂǂƃA�z�Ȍ�����𑱂��Ƃ�B
����͑����b�A���������Ƃ����ꑊ�ΐ����_�����藧���Č������Ƃ��B �����猩�Ă�ƂȂɂ��c�_���Ă�̂����番�����
�咣���܂Ƃ߂Ă���c
>>147
�c�_�̑Η��_��
�u�o�q�̃p���h�b�N�X�͓��ꑊ�ΐ����_�̔��e�v
�u�o�q�̃p���h�b�N�X�͓��ꑊ�ΐ����_�̔��e�ł͂Ȃ��v�Ǝ咣���Ă�z�������̎咣��ʂ����ߖ��������ݒ�����˂���Ă邾�� >>144
�����Ă��݂́u�R�v�ƈӌ�����v�����悤�Ɍ��������悤�Ƃ��Ă邪���ۂ͂܂������t�B
�ނ�>>16 �ɏ����Ă���Ƃ���u�����n�͏d�͏�Ɖ��߂��Ȃ��v�Ƃ�����Ɠ��ӌ��B
17�Ō����Ă���悤�ɁA�ʂɂ���ȉ��߂����Ȃ��Ă�������̂őS�����Ȃ��B
21�Ō����Ă���悤�ɁA�����������g���ΌZ��̉����n���d�͏�Ɖ��߂��邱�Ƃ��ł��邪�A����͑o�q�̃p���h�N�X�ɕK�{�ł͂Ȃ��B
22�Ō����Ă���悤�ɁA���ꑊ�Θ_�Ŕ��n���������Ƃ���Ɛ����閵���v�Ƃ��͌��Lj�؎�����Ȃ������B
27�Ō����Ă���悤�ɁA��i�ɑ�������{�[���j�������ɓ����Ď��R������������ɉ��ς����̂͂��O������ɂ���Ă邱�ƁB
���ׂĉ��Ɠ��ӁB >>148
�Ȃ�قǁA�o�q�̃p���h�b�N�X�͂Q�l�̌n��ΏۂɈ����Ă��邱�Ƃ����ŁA���͑Ώ̂ł͂Ȃ����E�����ƂɌŗL�����قȂ邱�Ƃʼn�������̂œ���͈̔͂ŏ\������
�C�ӂ̎���őo�q�̃p���h�b�N�X�̂悤�Ȑݒ������Ε��R����Ő��l�I�ɂ͐����ł��Ȃ��Ⴊ������ł����邪�킴�킴��������Ӗ��͂Ȃ�
��ʑ��Θ_���ƂQ�_�����ԑ��n�����قȂ�ŗL�������Ă�̂ʼn����x�̗L���Ƃ�����Ώ̐��Ő����ł��Ȃ��p���h�b�N�X������ȁA�Ƃ������V�����_�[�^�̉F���ł��ł��邩 ���������A�o�q�̃p���h�b�N�X�Ȃǂ����������R�Ȏ���O��ł̘b�ł����āA�킴�킴�d�͂̊T�O���������ޕK�v���Ȃ��B
����͈̔͂ŏ[���B
�o�q�̃p���h�b�N�X�͉������邽�߂ɔ��n��K�v�Ƃ���悤�ȃp���h�b�N�X�ł͂Ȃ��B
������o�q�̃p���h�b�N�X�͓��ꑊ�Θ_�����Ŏ��������B
>>150 151
��Ŏv�l��~����̂��w�ǂ̖}�l�]�~�\�������
�O���[�o���Ȋ������W�n����ɂ���]�����_�ɒ����^����N�������V�˃A�C���V���^�C�����B
���ꑊ�ΐ����_�����Ȃ�A�C���V���^�C���łȂ��Ƃ����̕����w�҂��������Ă���B >>153
�X�ɏ]���̃j���[�g���͊w�����ɂ��Ă�`������ł��A���C�Ŕ��n���猩��
���S�͂�R���I���͂��������ł��g���Ă�A�������Ă邩�ǂ����ʂ����B
���n����ɂł��Ȃ����ꑊ�Θ_�ɑ���A�C���V���^�C���̖���N�͓��R
���_�𗝉��ł��邩�ǂ����ʂ����B �܂����Ⴂ���Ă�̂��B
�P�Ȃ���n�Ȃ����̘g���o�Ȃ��B
���������Ɠ��ꑊ�Θ_�Ŗ�肪������Ǝ咣����l�����邪
���ꑊ�Θ_�ɂ͓��������������A�������������_�Ƃ��Ċ������Ă���B
����ɓK���ȉ����h���������h��t������������͘_���I�ɊԈႢ�ł���B
�������炯�̑��Ԃ̂����Ɠ����ł���A���Ԃ��Ȃ��Ȃ�����
�����������g���Ȃ疵����������ʑ��ΐ����_���痝�����ĉ����̂��������B
>>155
�L�~�͘_�����_�̊�{�������ł��Ȃ��悤���� >>153-154
�A�C���V���^�C������ʑ��Θ_���l�����̂́A
���ꑊ�Θ_�ŏd�͂������Ȃ�����ł����āA
���ꑊ�Θ_�Ŕ��n�������Ȃ�����ł͂Ȃ��B >>158
���x�J��Ԃ��Ă������ł��Ȃ��]�̐l���H
���ꑊ�Θ_�Ŕ��^���������Ȃ��̂ł͂Ȃ��B
���n�̐Î~��Ԃ���ϑ��������̉^���������Ȃ��̂���B >>156 >>159
�n��������l�H�q�����̏�g�����猩��ΐÎ~��Ԃł�����
�u�n���̖��L���͂Ɖ��S�͂��肠���Ė��d�͏�Ԃł���v
���w���ł������������ł���B
���ꑊ�ΐ����_�����ł͏�L�̗l�ȉ�㈐��_���ł��Ȃ��̂ł���B >>159
�Ȃ猾�������悤�B
�A�C���V���^�C������ʑ��Θ_���l�����̂́A ���ꑊ�Θ_�ŏd�͂������Ȃ�����ł����āA
���n�̐Î~��Ԃ���ϑ��������̉^���������Ȃ�����ł͂Ȃ��B >>161
>���n�̐Î~��Ԃ���ϑ��������̉^���������Ȃ�����ł͂Ȃ��B
�ف`
��łɎ咣����Ȃ�o���ꑊ�ΐ����_�̉�㈂����v��
��ԊȒP�ȁA�������x�^���̐Î~��Ԃ���ϑ������u�����n�̎��Ԍo�߁v��
�������Ă���Ȃ��� >>162
�⑫
�菇�����̐����ł��\����B >>162
>>94���܂��ɂ��ꂾ��B
�Ƃ������A���n�̐Î~��Ԃ���ϑ��������̉^���������Ȃ��Ƃ����̂��^�ł��낤���Ȃ��낤���A
����̓A�C���V���^�C���̓��@�ł͂Ȃ��A�ƌ����Ă�����ǂȁB >>161
�ȒP�Ȍv�Z�菇�����ł���������̂���A���ꂷ��ł��Ȃ��̂��H
����Ƃ��_�j�����̂��|���̂��H >>164
>>94
������Ċ����n����ϑ������v�Z���A���n����ϑ������Ə̂���
�]�p���Ă邾������B >>165
�������̑��ΐ��ƃ~���R�t�X�L�[�������g���āA�����ƈʒu�����肷�邾������B
>>166
>���n����ϑ������Ə̂��ē]�p���Ă�
�ǂ������Ӗ����H >>164 >>167
�L�~�̔��n���Î~�Ə̂���菇�Ƃ�
�����n���Î~�̎��Ԍo�߂���������x�^���n�̎��Ԍo�߃т��v�Z������
�����x�^���n���Î~�̎��Ԍo�߃т��猩��A�����x�^�����銵���n�����Ԍo�߂�
���Ɠ���ւ��Ă邾������H
�����x�^���n���Î~�̎��Ԍo�߃т���A���ꑊ�ΐ����_�ł͒��ڌv�Z�ł��Ȃ���
�����Ӗ�������Ȃ��̂��H >>168
���̂������B�ꐳ�������@���낤���B
������������Ȃ����̂����z���Ă���H >>153
���܂�A�ȂɌ����Ă邩�킩��Ȃ���
���Ƃ킩��ɂ������疼�O���ɖ��O�����Ă��� >>170
>>167 167 169 ����L�~�̌v�Z�菇�̐����ɂ����
���n�Î~���瑼�n���v�Z�����H�Ə̂���Ӗ�������������\���B >>168
>�����x�^���n���Î~�̎��Ԍo�߃т���A���ꑊ�ΐ����_�ł͒��ڌv�Z�ł��Ȃ�
>�Ƃ����Ӗ�
�����x�^���n���Î~�̎��Ԍo�߃т���A�f�����x�^���Ɍ����銵���n�f�̂���
���ꑊ�ΐ����_�̃��[�����c�ϊ������Œ��ڌv�Z����� ��<�тŖ�������B
�i�o�q�̃p���h�b�N�X�j
�����������Ă������ł��Ȃ���Ŕ]������̂��s�v�c���B �����Ă��܂��Έ�ʑ��Θ_�����āA���n�������ɂ���Ċ����n�ɕR�t���ċt�Z���Ă��邾�����Ƃ����̂�
>>156
���Ƃ͑o�q�̃p���h�b�N�X�̂��ƁH
���������͂���Ȃ����A�Ȃ�ł����Ȃ�o�Ă����� >>173
���ꑊ�ΐ����_�ɂ͓��������������@���� >>174
�����x�n����v�Z���Ȃ����p���h�b�N�X�i�����j�ɂȂ��H
����������̂� >>174
����Ƃ�����̎��Ԍo�߂��Ⴄ�����Ńp���h�b�N�X���Ƃł����������̂� >>176
�����x�n�ɓ��������͂���Ȃ����A�ʓ|�Ȃ̂ʼn����x�n�̑��݂��Ȃ��o�q�̃p���h�b�N�X���o������ >>176
�����x�n����v�Z�����疵������̂���H >>180
���[�����c�ϊ��͉����x�n�Ɗ����n��ϊ��ł��Ȃ��B
�����𗝉����ď����Ă�̂��H ���ꑊ�Θ_�f�l�̃p���h�b�N�X: �@���Ή^���Ō݂��Ɋϑ�����̎��Ԍo�߂��x���
���ꑊ�Θ_���S�҂̃p���h�b�N�X�F���Ή^���ŕЕ��i�Z�j�������Ԍo�߂�����I�ɒx���
�o�q�̃p���h�b�N�X�͌�҂̕�����
�ǂꂪ�N�̔������킩��˂���
���e���Ӗ��킩��Ȃ�������e���琄���ł���
>>177
�O�̂��߃p���h�b�N�X�̒�`���肢���܂�w �f�l�[�����S�ҁ@�ɃO���[�h�A�b�v���đ��Ή^���Ō݂��Ɋϑ�����̎��Ԍo�߂��x���
���p���h�b�N�X�i�����j�ƔF�����Ȃ��Ȃ������x���̐l��
���Ή^���ŕЕ��i�Z�j�������Ԍo�߂�����I�ɒx���Ƃ������ʂɂ����
�p���h�b�N�X�i�����j�ƔF�����Ă��܂�㩁B
>>165
�ϑ��҂ɓY�������ȊO�͓K���ɍ��W�n�����
�v�ʂ�����������̍��W�n�ŏ�������
����� >>186
������ꑊ�ΐ����_�����̉�㈌v�Z�łȂ����� >>186
������ꑊ�ΐ����_�͊����n���犵���n�ւ̍��W�ϊ������F�߂��Ȃ�
�A�C���V���^�C����������������B >>188
�N�������Ă���Ƃ��͂Ƃ肠�����u���Ă����āA
�K���ȍ��W�n�ŕ��������������������̂͌��̕������Ɠ����ł���
����͂����ł����H�e���\���Ƃ��̕ϊ����Ȃ͗������Ă�킯����� >>185
����Ԃ�����
���n��ɔ��ł���~���[�I���̕�����������т镨�����ۂ�
���ꑊ�Θ_���S�҃��x���̑��Ή^���Ō݂��Ɋϑ�����̎��Ԍo�߂��x���
��������ł���n��̊ϑ������ł���B
�o�q�̃p���h�b�N�X�̗ނƊ��Ⴂ���Ă�l������̂ŊԈႦ�Ȃ��悤�ɁB >>189
>�K���ȍ��W�n
���̃X�����X����ł͂���̐��������Ȃ�ł���B >>191
�K���Ƃ����̂͂Ȃ�ł������Ƃ����Ӗ� >>193
>�C�ӂ̍��W�ϊ�
���ꑊ�ΐ����_�ł͊�͊����n������
�����n���犵���n�@�܂��́@�����n����u�ԑ��x�����݂�����n�ւ�
�u�ԓI�ȃ��[�����c�ϊ��݂̂��F�߂���B
�܂�A���n����̓��[�����c�ϊ����F�߂��Ȃ��̂�
���n�ł���Z�̃��P�b�g������v�Z����ƃp���h�b�N�X�i�����j���N����B >>194
�������������ł��邩�ۂ��ɓ����Ă������� >>146
>���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��B
����͉R
���O�Ƃ̔F���̃Y���͂����ɂ������悤����
�u3�v�Ɖ��͂����F�����Ă����̂�>>11�̂悤�ɓ���������p���ďd�͏������Ă��� ���I�Ɉ�l�ȏd�͂͏d�͂łȂ��Ƃ����I���W�i���ȏd�͂̒�`�͕s�v
���R�Ȏ���͖ܘ_�A�C���V���^�C���������̉��Ɋ܂܂�Ă��邩���
�����̗����̍��ɂ����>>146�̂悤�Ȋ��Ⴂ���N�����̂� �Ŏv�l���������牽�ł�����Ƃ����̂��I�O��
���̂Ȃ�A�C���V���^�C���������̉��ł���悤�ȏd�͏��I��ł���̂Łu�����I�ɂ��蓾�Ȃ��d�͏�v�����肵�Ă�킯�ł��Ȃ�
���̕ӂ́u3�v�ƔF�����p�ł��Ă����̂�>>11�ł͂���ȓI�O��Ȏw�E�͂Ȃ�����
�܂��v�l�����Ƃ������@�_�ɂ��Ċw�ق��������� �n�����l�d�͏�Ƃ��ĉ����������l����v�l�����̃��f���͉��ł��L��̃��f���ł͂Ȃ��̂�
�����Ɨ��_�ɐ����������f�����ł����Ă�������i�q���v�̒n��ϑ��ł��d�̓|�e���V����������h�ő������肷��
���I�Ɉ�l�ȏd�͏�͓��������ŏ�����̂������������ꂪ�A�C���V���^�C�������������d�͏�Ȃ̂�����
����𗝉��ł��Ă��Ȃ��������߂�>>146�̂悤�Ȋ��Ⴂ���N������ >>196-199
���{�I�Ȗ��́A���݂����̖��͓��ꑊ�Θ_�ł͂Ȃ��ƌ������������߂ɁA�Ӗ��Ȃ��u�d�́v��u���������v�Ƃ����T�O��t�������ĕʂ̖��ɂ��Ă��܂��Ă��邱�Ƃ��B
17,21,156,174,175,178�炪����w�E���Ă���悤�ɓ��ꑊ�Θ_�Ő����ł���b�ɂ킴�킴�����������������Ӗ����Ȃ��B
�������>>11���������ނ����̌コ���w�E�����Ă���B�ނ͂��݂Ƃ͂܂��������Έӌ�����B
���݂̂킪�܂܂ɍ��킹�Ĕނ��b�����s���̂������X���������ė��p����̂͂�߂Ă���B �����āA>>161�������Ă���悤�ɁA
���ꑊ�Θ_�ň����Ȃ��͔̂�ψ�ȏd�͏ꂾ�B
���R�Ȏ���łȂ�ϑ��҂�������������悤���A���S�ɓ��ꑊ�Θ_�̊T�O�����Ōv�Z�ł���b�ɂȂ�B
>>94-95�ɔ��n���猩���n���̉^���̃O���t�������ł��傤�B
���̌v�Z�Ŏg���Ă���v�Z�͏����ɓ��ꑊ�Θ_���B
���n���猩�����̂̉^���������ɓ��ꑊ�Θ_�݂̂ŋL�q�ł��邱�Ƃ����m�ɕ�����B
���ꑊ�Θ_�������牉㈓I�ɓ������b�ɑ��A���ꑊ�Θ_�Ő����ł��Ȃ��Ƃ������݂̎咣�͔j�]���Ă���B ���Ȃ݂ɂ��݂̎�̎v�l�����ŁA�������ɑ��I�Ɉ�l�ȏd�͂������Ă���ƍl���Ă݂�͍̂D���ɂ���悢���B
���R�Ȏ���ł�����Ƃ���œ��ꑊ�Θ_�Ōv�Z�����̂Ɠ������ʂɂȂ�B
�o�q�̃p���h�b�N�X�͓��ꑊ�Θ_�Ŏ������Ƃ������Ƃ��킩��ł��傤�B
�܂��ǂ����Ă������x�n�ŋL�q�ł��Ȃ��Ǝv���Ă�݂����ŗ��R���߂��Ⴍ���Ⴞ����ǂ����悤���Ȃ�
����ɂ������Ȃ��A�c�_���鎑�i�̂Ȃ��l�Ԃ���
�����x�n�ł�����̌i�F�͌����邵����͓��ꑊ�Θ_�̘g���ł̉����x�n�ɂ����鐢�E�̋L�q�̈�ɑ��Ȃ�Ȃ��Ƃ���������O�̘b
���
��ԕ����Ɏ������E�����̓�����1+1����(���R)������l����
����n�_����Z�͐��̕����ցA�핉�̕����ցA���قȂ鑬�x�Ői��
�Ăяo������n�_�ł�(�ꎟ���Ȃ̂ŕK���o�)2�l�̌o�ߎ��Ԃ͂ǂ̂悤�ɂȂ邩�H
�܂��A�Z���猩���ꍇ�A�킩�猩���ꍇ�A���ꂼ�ꑊ��͓������x�ŋ�Ԃ�������Ă���悤�Ɍ�����̂ő���̕����o�ߎ��Ԃ��Z���͂��ł���
���̃p���h�b�N�X�͂ǂ̂悤�ɉ�������邩�H
>>204
>�Ăяo������n�_�ł�(�ꎟ���Ȃ̂ŕK���o�)2�l�̌o�ߎ��Ԃ͂ǂ̂悤�ɂȂ邩�H
2�l�̌o�ߎ��Ԃ͓����B
>�܂��A�Z���猩���ꍇ�A�킩�猩���ꍇ�A���ꂼ�ꑊ��͓������x�ŋ�Ԃ�������Ă���悤�Ɍ�����̂ő���̕����o�ߎ��Ԃ��Z���͂��ł���
�������̑��ΐ��ɂ��A��ԕ����̎����̈����ɂ��鑊��̎����͉��ʂ𗚂��Ă���B
����̌o�ߎ��Ԃ̒x���͂��̉��ʂɂ���đ��E����A�ĂьZ�킪�o������Ƃ��̌o�ߎ��Ԃ͓����ɂȂ�B >>205
�Q�l�̑��x���قȂ�_�ɒ��ӂ��Ă�����x�l���Ă�������
�Е����Î~���Ă���ꍇ���킩��₷�� >>206
>�Q�l�̑��x���قȂ�_
���S�Ɍ����Ƃ��Ă����B
����Ȃ�悸�A���镨�̂��������֓����Ɍ�������A��Ԃ���������������̂܂Ŗ߂��Ă���̂������������Ƃ��ɁA
���̕��̂̉^�����u��ΐÎ~�v���Ă���ƒ�`����B
��ΐÎ~���Ă��镨�̂ɑ��鑊�Α��x�̑傫���̑召�ɂ���ČZ��̌o�ߎ��Ԃɍ����t���B
��ΐÎ~�ɑ��鑊�Α��x���傫�������o�ߎ��Ԃ��Z���Ȃ�B >>200
����u�i���ꑊ�ΐ����_�Ɋ܂܂�Ȃ����������ŏd�͂���������j���ꑊ�ΐ����_�Ő����ł���v���
>>11�͂܂��ɂ������Đ������Ă�킯������
�����������܂܂Ȃ����ꑊ�ΐ����_�ň�l�d�͂�������Ȃ�>>4�ɑ��Ĕ�I����悩����
�������Ԃ��Ă���������>>11������
�N���o����Ȃ炵�Ă݂�悢
�܂�>>146�̂悤�Ȍ�������Ă鎞�_�őO��m���̃Y�������������Ƃ����������̂Ŗ��Ӗ����낤����
��l�d�͏�̓A�C���V���^�C���������̉��ł��������Ƃ����d�͂Ȃ��
�������N�ɂ��Ƃ���͏d�͂����݂��ĂȂ��炵���̂ŃY�����������̂��낤 >>202
���̖�̉�>>11�ŗ^�����Ă�̂�
���������ɂ���Ĉ�l�d�͂��������ē��ꑊ�ΐ����_�ɋA��������
��͍D���ɍ��W�ϊ��������
�����ŏI������b >>208
����A����͂��݂�����Ɂu�i���ꑊ�ΐ����_�Ɋ܂܂�Ȃ����������ŏd�͂�t���������v��肾����ˁA
���������������������ŏd�͂��������Ȃ���Ȃ��̂�����܂�����ˁB
�����ʼn��ď����̂��}�b�`�|���v�Ƃ����B
���S�ɂ��݂̕����ł��B�����ɂ��݂͂�������Ƃ��ƂƓP�ނ��Ă��������B >>207
�����ł���
�ł͂��݂����猩������̉^���������Ȃ̂ɂ��ւ�炸�o�ߎ��Ԃɍ������܂��̂͂Ȃ��ł����H ��������Ȃ����������邩�炾��jk
>>211
>���݂����猩������̉^���������Ȃ̂�
����{�����ȁH
�ȂႤ�悤�ȋC�����邼�B >>210
���[����������
>>4�ɑ��Ė{���̓{�[�����Î~���Ă��ČZ���������Ă�ƌ�����Ɠ�����
���ǁu���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����l���̐l�Ƃ͕����肠���Ȃ��낤��
�m���ɂ��̎v�z�Ȃ�{�[�����Î~���Ă��Ă���̂��^���Ȃ낤��
���̐��E�ɂ͏d�͂��Ȃ��炵���̂ŏ���ɏd�͂�t���������ČZ�������������Ă邱�Ƃɂ����ƂȂ�킯��
��芸�����F���̃Y���̌����ӏ����u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�ɂ��邱�Ƃ����������̂ʼn���� >>213
����������Ɩ������邩��Ⴄ���A�C������ł����܂��œ��������Ă��܂��ėǂ��ȁH ���ۂɁu���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����������̗p�����>>4�������������ݒ莩�̂����z�d�͂Ȃ���̂����肵�Ă����ƂɂȂ邵��
���ݒ�̒i�K�œ����������g��ꂽ���ƂɂȂ�̂œ��������ŏ������Ă�����͂Ȃ�����A��
�Ȃ�قǂ˔F���̃Y�������S�ɕ��������� >>216
���̂��A���������Ă���Ȃ����� >>215
���������Ă��܂��ėǂ���B >>218
�I�b�P�[�ł�
�������E�����̂����Ŏ���Ƀ��[�����c�Ώ̐����Ȃ�
���ꂪ�Q�l�̊����n����Ώ̂ȗ��R�A���������ăp���h�b�N�X�͂Ȃ�
��̓I�ɂ́A>>205�Ŏw�E���Ă��ꂽ�悤�ɌZ���猩�Ĉ����̒�̎��v�͍ŏ�����i��ł���A�����ċ�Ԃ̃��[�����c���k�����邽�ߓ������x�Ői��ł��o�ߎ��Ԃ��Z���A���̂Q�_
��������ȋ�̓I�v�Z������K�v�͂Ȃ��� >>219
����A��ԓI�ړ������͒Z���ł͂Ȃ������Ȃ�
�����x�n���l�����Ƀp���h�b�N�X���������Ă��܂����@�͂��������܂� ���������Θ_���S��(eman�S���ǂ��x)�����ǁA�o�q�̃p���h�b�N�X�̋c�_�ɂ��ē��ꑊ�ΐ����_�͈̔͂���Ȃ������������C������B
�u�Z���猩��Βn�����������Ă邯�ǁA����͓��ꑊ�ΐ����_�ň����Ȃ���Ȃ����v �ɑ��Ă݂�Ȉ�������Č����Ă邯�ǂǂ����̂������Ăق����B
�����͍��̂Ƃ���O���t�Ŏ����ꂽ��ȊO�o�Ă��ĂȂ��Ǝv���B ���̃O���t�Ɋւ��ẮA�n����őS�Ă̌v�Z�����āA��������Ɂu�Z����͂��������Ă�͂����v���Č����̂��O���t�ɂ��Ă邾�������Ďw�E����Ă邯�ǂ���ɑ��锽�_���o�Ă��ĂȂ��悤�Ɏv���B �u��ʑ��ΐ����_�����Ċ����n�Ɋ��Z���Ă邾���v�݂����ȃ��X��1���������ǁB
�u�d�͂�����ɓ������Ă邾���v�Ƃ����ᔻ���������ǁA���ΐ����_�Ŋ����͂Əd�͓͂����Ȃᖳ���́H�����Ⴄ�Ȃ���ꑊ�ΐ����_�Ŋ����͂͂ǂ�������́H
������Ȃ����͈̔͂��ă��X���������ǂ���Ȃ�c�_�̗]�n�͖����Ǝv���B����ƈ�ʂ̐蕪��(���x�����O)�̖��ł��������B �ł��A�����������o�Ă���Ȃ���ꂶ��Ȃ����ă��X�����邩���ѐ��͖����悤�Ɏv���B
�܂�A�������������ŌZ��ł̒n���̎��Ԃ���ꂾ���Œ��ڌv�Z������@����Ă��炢�����B���̂��߂ɂ͌Z�̍��W�n����n���̍��W�n�ɍ��W�ϊ����Ȃ��ƍs���Ȃ��Ǝv���B
>>221
��Ԓ��ٓI�Ȃ͎̂O�̊����n���g�������x�n���������@

�����x�n���猩���L�q�͂܂���� >>221
�Ƃ肠�����A�o�q�̃p���h�b�N�X��2�l�̊Ԃ̔�Ώ̐������ʼn�������邱�ƁA
���ꑊ�Θ_�Ƃ͕��R�ȃ~���R�t�X�L�[�����̗��_���w�����ƁA
�����Ȃ銵���n�ł����ꑊ�Θ_���L�q�\�Ȃ��ƁA
��Wikipedia�ɋL�ڂ���Ă��邱�Ƃ������Ă���(�����Ƃ����L�����������Ƃ͎v�����K���ɒT���Ă���)



���銵���n����ʂ̊����n�ւ̓��[�����c�ϊ��Ō��т��B
�����x�n�Ƃ����ǁA����u�Ԃɂ͂��鑊�Α��x�����������W�n������A
���̍��W�n�Ƃ̓��[�����c�ϊ��Ō��т��B���̑��Α��x�����X���X�ς��Ƃ��������B
���Α��x�����X���X�ς��悤�ȃ��[�����c�ϊ������X�q���Ă����Ή����x�n�ւ̕ϊ��͊����B
��̓I�ɒm�肽��������[�̋��ȏ��ł�����
���̎葱���Ŗ��炩�ɂȂ������ɏd�v�Ȍ��ۂɃg�[�}�X��������B
���̓��o�Ɉ�ʑ��Θ_�Ȃǎg���Ă��Ȃ��B
>>221
�h�Z����͂���������͂����Ƃ����̂��O���t�ɂ��Ă��邾���g
�����n������n���ϑ����Ă݂�A�Ⴆ�ΌZ�����v�����Ă���̂�킩��ϑ�����
�����͑S�Ċ����n�ł̖@���ɏ]���Ă���͂���
���������āA�Z�����n�łȂɂ��ϑ����邩�͊����n�ł̖@�����牉㈂ł���
����������͂����A�ł͂Ȃ��A�����łȂ�������Ȃ��A�̂�
���������̂���ʍ��W�ϊ��₻�̉��ł̃e���\���Ȃǂ̕ϊ��@���� ���ꑊ�Θ_�łł��Ȃ��ƌ����z�͓��ꑊ�Θ_���g�����Ȃ��Ȃ��z����
��ʑ��Θ_���킩��킯���Ȃ�
>>223
�~�X�A�����Ȃ���n�ł��c����
���Ȃ݂Ɉꖇ�ڂɃA�C���V���^�C�������������Əd�͏�ɂ�鎞�Ԃ̒x��Ő��������݂����ƂɌ��y������ >>221
�L�~�̎w�E�͐������B
�������W�n�i�Î~�j���烍�[�����c�ϊ��Ŕ��n�i�������x�A��]�^���Ȃǁj���v�Z�ł���B
���ꂪ�u���ꑊ�Θ_�Ŕ��n��������v�Ƃ����Ӗ����B�����N���ے肵�Ă��Ȃ��B
���ꑊ�Θ_�̘g�������ł͔��n�i�Î~�j���瑼�̍��W�n�Ƀ��[�����c�ϊ��ł��Ȃ��B
�Ƃ������e�������ł��Ȃ��l���A�����Ă邪�A���[�����c�ϊ��ł���Ǝ咣������@������ւ��̃f�^�����B >>227
>��ʍ��W�ϊ��₻�̉��ł̃e���\���Ȃǂ̕ϊ��@��
����͓��ꑊ�Θ_�̗��_�̘g�O�ł���B�@���̋�ʂ��ł��Ȃ��l�����邾���B >>230
���n�i�Î~�j���瑼�̍��W�n�Ɉ�ʍ��W�ϊ����邽�߂�
�������������_�\���ɂ͓��������Əd�͏ꂪ�K�v�ɂȂ�B
���R�A���ꑊ�Θ_�̗��_�̘g���ɂ͓����������d�͏�������B >>231
�v�ʂ��t���b�g�̘g���ō��W�ϊ��ƃe���\���v�Z�����邱�Ƃ͓��R�ł���
����͓��ꑊ�Θ_�̔��e
�����ƌ����A�j���[�g���͊w��(��ԓI)��ʍ��W�ϊ��ƃe���\���v�Z�����l �ǂ�����ʍ��W�ϊ��ƈ�ʋ��ϐ����������Ă���悤�Ȋ�����
>>232
�A�C���V���^�C���̌������e�ɂ��Ɠ��ꑊ�Θ_���\�̒���ɔ��n�ւ̊g����
�l�@�������A���̗l�ȍ��W�ϊ��́u���R�����œ����ɗ�����Ƃ����o�����v�Ɩ���
���邱�Ƃ������B�Ə����Ă���B >>230
���[�����c�ϊ��͐��`����������x�n���]�n�ɂ͕ϊ��ł��Ȃ����c
����A��B���ł����B��A���ł����ˁc�t�ϊ����Ēm���Ă܂����c >>236
>���[�����c�ϊ��͐��`����������x�n���]�n�ɂ͕ϊ��ł��Ȃ����c
�o����A�ϊ��̌v�Z���@�̓O�O��ڂ��Ă�B
�܂�
�������W�n�i�Î~�j���烍�[�����c�ϊ��Ŕ��n�i�������x�A��]�^���Ȃǁj���v�Z�ł���B
>A��B���ł����B��A���ł����
��̌v�Z���@�ł͋t�́i�����Ȃ��j�o���Ȃ��B
���n����̓��[�����c�ϊ����ł��Ȃ�����A���ꂪ�����ł��Ȃ��l������B ���[�����c�ϊ��͐��`�ł����H
������A�����n��������x�n�ւ̕ϊ��͐��`�ł����H
>>237
�O�O����Ă̂͂��Ȃ胄�o���̂ŁA�ڂ��Ă��鋳�ȏ��������Ă������� >>239
������ƃO�O��Γ��ꑊ�Θ_�̃C���`�L�łȂ����[�����c�ϊ��̌v�Z���@���ڂ��Ă�
�܂�
�����n�i�Î~�j������^�����u�ԓI�ȑ��x�̊����n�i���`�j�Ƃ��Đϕ��v�Z����B >>241
�⑫�A���̗l�ȃ��[�����c�ϊ��̌v�Z���@�́A���n�i�Î~�j����ł��Ȃ��̂��N�ł�����B >>241
����̓��[�����c�ϊ��Ƃ͌���Ȃ��̂ňȍ~�������ĉ����� >>241
�����ċt�ϊ������݂��Ȃ����R�͂Ȃ�ł����H
���R�r�A�����k�ނ��Ă��Ȃ����(���Ȃ��Ƃ��Ǐ��I��)�t�ϊ��͑��݂��܂����c >>221
> �Z���猩��Βn�����������Ă邯�ǁA����͓��ꑊ�ΐ����_�ň����Ȃ���Ȃ���
�Z��̍��W�n�͊����n�ł͂Ȃ��A�Ƃ��������ŕʂɓ��ꑊ�Θ_�������n���������Ȃ��Ȃ�Ă��Ƃ͂Ȃ��B
�ȑO�ɂ����������ǁA���ۂ�������W�n�ŋL�q����Ă���Ƃ��A���ꂪ�ʂ̍��W�n�ł͂ǂ��L�q����邩�͏�����
���w�̖��Ȃ̂Ŋ����n��������̂ɑ��̍��W�n�͈����Ȃ��Ȃ�Ă��Ƃ͂Ȃ��B
�����^���̍��W�n�Ƃ��Ă�>>6�ŗ�������Ă���B
> �n����őS�Ă̌v�Z�����āA��������Ɂu�Z����͂��������Ă�͂����v���Č����̂��O���t�ɂ��Ă邾��������
����̉��������̂��킩��Ȃ��ȁB
>�u�d�͂�����ɓ������Ă邾���v�Ƃ����ᔻ���������ǁA���ΐ����_�Ŋ����͂Əd�͓͂����Ȃᖳ���́H�����Ⴄ�Ȃ���ꑊ�ΐ����_�Ŋ����͂͂ǂ�������́H
���ꑊ�Θ_�͏d�͂�����Ȃ��̂�����u�����͂Əd�͂������v�Ȃ�Ęb�͏o�Ă��Ȃ��B���ꑊ�Θ_�ł͊����͂͂����܂ł������́B
�����n�ł͂Ȃ����W�n���g�����Ƃɂ���Đ����錩�����̌��ʁB
�o�q�̃p���h�b�N�X�͏d�͂Ƃ͊W�Ȃ��b�Ȃ̂œ��ꑊ�Θ_�ŏd�͂������Ȃ��Ă��������Ȃ��B
�����������n�łłĂ��銵���͂ɓ������������ďd�͏���ŌZ���Î~���Ă��Ē킪���R�������Ă���Ɩ��𑨂������͎̂��R���B
���̏ꍇ�͓��R�i���Ȃ��Ƃ������ȁj���ꑊ�Θ_�͈̔͂���͈�E����B���Ⴀ��ʑ��Θ_���ƌ����Ƃ܂����������܂���ʑ��Θ_�Ɉ�����ݓ����Ă�B
>>6�Ɏ������悤�Ȉ�l����������W�n�ł͉��������̑O���ɍs���قǎ��Ԃ������A����ɍs���قǒx���i�ށB�����܂ł͓��ꑊ�Θ_�͈̔́B
�����ɓ������������ĉ������W�n���d�͏�Ƒ����������ƂŁA�d�͏ꒆ�ł͏�ɍs���قǎ��Ԃ������i�݉��ɍs���قǒx���i�ނ��Ƃ��������B
�A�C���V���^�C����1907�N�ɂ��������l�@�����Ă��Ă��ꂪ��ʑ��Θ_�ւ̑����B���������ʑ��Θ_�ɂ��ǂ蒅���ɂ� 1915�N�܂ł��������B >>245
>> �n����őS�Ă̌v�Z�����āA��������Ɂu�Z����͂��������Ă�͂����v���Č����̂��O���t�ɂ��Ă邾��������
>����̉��������̂��킩��Ȃ��ȁB
�L�~���g�������v���Ă邾���ŁA���l�͂����͎v��Ȃ��B
���l�͒N�������X�����悤�� A->B �Ȃ�� B->A ���Γ��ϊ��ɏo���Ȃ���Εs���S��
�ƍl���Ă邾���B ���肪�Ƃ��B�m���ɋt�ϊ����ł���͂�����ȁB
> A->B �Ȃ�� B->A ���Γ��ϊ�
�Γ��ϊ��Ƃ����̂���̓I�ɉ��������Ă�̂��킩��Ȃ��ȁB
�����n���m�̃��[�����c�ϊ��Ƌt�ϊ��݂����� v �� -v �����ւ��邾���݂����Ȃ��Ƃ����҂��Ă���킯����Ȃ���˗��ɁB
�o�q�̃p���h�b�N�X�Œ�̗���ƌZ�̗���͑Ώ̂���Ȃ����炻��Ȃ��Ƃ͂��肦�Ȃ����Ƃ��炢�͗������Ă��ˁH
>>221
> ���������Θ_���S��(eman�S���ǂ��x)�����ǁA
����Ȃ�b�͑����B
eman�ɋȂ����Ă��Ȃ�����̉����x�n�Ɉ�ʑ��Θ_�ȂǕK�v�Ȃ����͏����Ă���B
�@https://eman-physics.net/relativity/uni_accel.html
�u�����ɂ���ċ[���I�ȏd�͂������Ă����Ƃ��Ă�,����͋Ȃ����ĂȂǂ��Ȃ��Ƃ������Ƃ�. ����͒N���猩�Ă��Ȃ����Ă��Ȃ�.
���,�^�̏d�͂����鎞�ɂ͎���͋Ȃ����Ă���.�N���̎��_�ɂ�錩���������̘b�ł͂Ȃ���,�m���ɋȂ����Ă���.
����̘b�ł�,�Ō�Ɉ�ʑ��Θ_�ɓ��Ă͂߂Ċm�F���Ă݂�����ǂ�,����ȊO�ł͈�ʑ��Θ_�̒m���͉����K�v�Ȃ��̂�����.�v >>221�@���łɁA
> �O���t�ɂ��Ă邾��
�����A���ꑊ�Θ_�̒m�������ł������芵���n�̔��n�̕ϊ����s���āA�O���t�ɂ��ł�����Ă��Ƃ��B
�ނ��돬�w���ł��킩��悤�Ȗ��m�ȃO���t�����ĉ��őʁX�����˂Ă�̂��������Ă���B
> ���ꑊ�ΐ����_�Ŋ����͂͂ǂ�������́H
�����͂͊����͂��ˁB
���Z�œd�Ԃ��}�u���[�L�|���Ă�̂߂�̂��ďd�͂�����������ďK�����̂����H
�j���[�g���͊w�ł����ꑊ�Θ_�ł��͊����͂͊����́B
> �܂�A�������������ŌZ��ł̒n���̎��Ԃ���ꂾ���Œ��ڌv�Z������@����Ă��炢�����B
�O���t�̉摜�ɂЂƂƂ��蒼�ڌv�Z���Ă鎮�͌����Ă��Ǝv�����H
�ꕔ�̎����B��Ă邩�炻����������Ď��ł����̂��ȁH >>221
�o�q�̃p���h�b�N�X�͓��ꑊ�Θ_�͈̔͂���B
�p���h�b�N�X���\������v�f�����Ȃ̂��������Ă݂��B ���i�q���v����
���q�̐U�������v��������̂�����
�d�͂�^�������q�^���ɂ������钼�ړI�ȉe���ɂ��덷�����������Ȃ��́H
���ΐ����_�̗��Ɏg���Ȃ��Ǝv�����ǁB�ǂ��Ȃ́H
�U��q���v�g���đ��ΐ����_�̗����悤�Ƃ��Ă�Ƃ���Ȃ��B
>>221
�ނ́u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����v�������肵�Ă��邱�Ƃ����������i���̌�����v�����Ă��鑊�ΐ����_�̋��ȏ��͒m��Ȃ����j
�������̌������̗p����Ƒ��I�ɑł������邱�Ƃ��O��ƂȂ��Ă���̂Łu���������v�ŏd�͂��������ƂɂȂ�
�����Ă��̏d�͂������ꂽ���E���{���̐��E�炵��
���ꂾ��>>11���u���������v���g���Ă��邾���Ȃ̂œ��ꑊ�ΐ����_�Ȃ̂�
�F���̃Y���͂��̗v�����̗p���Ă��鋳�ȏ��Ŋw���ۂ����낤 ���̗v���̂��Ƃł�>>4�͋��\�̐��E
������u���������v�Ō��X�̐��E�i�{�[�����Î~���ČZ���������Ă���j�ɖ߂����Ƃ���n�߂邾��
�����܂łœ��ꑊ�ΐ����_�Ȃ̂�
��l�d�̗͂L���ł��ꂪ���X�̂��̂Ȃ̂��ۂ�����ʂł���炵��
���́u���X�v�Ƃ����T�O���l���Ă��Ȃ��̂ň�l�d�͂��d�͂ƍl����i�ܘ_�A�C���V���^�C���������̉��ɂȂ��Ă���j ��l�d�͂����݂��Ȃ��{���̐��E�ƈ�l�d�͂����炩�̑���ō��ꂽ���\�̐��E��2�̐��E�����݂�����Ă��Ƃ���
>>253-254
�ނ��ĒN����A���肪��l�����݂����Ɍ����ȁB
�܂������ɃY���Ă�B���\�̐��E�]�X�Ƃ������b�ł͂Ȃ��B
���ꑊ�Θ_�ōl���܂��傤���Č����Ă�Ƃ��ɁA���݂�����Ɉ�l�d�͂����肵���̂��u���̉��ρv�ɂ�����킯�B
������݂�Ȏw�E���Ă�킯���B
�Ȃ��Ȃ瓙��������m���Ă邫�݂ɂƂ��Ă͂܂������������̂��肩������A
�����������g���Ȃ����ꑊ�Θ_�̃X�^���X�ł͏d�͂������p���Ȃ��̂ł܂������ʖ��ɂȂ��Ă��܂��B
���ꑊ�Θ_�����ōl���܂��傤���Č����Ă�Ƃ��ɁA����ɕʂ̊T�O�������Ė������ς��āA�ق�����Ȃ��ł��傤�Ƃ����̂̓i���Z���X�Ƃ������b�B >>253
�ȗ���������Ƃ���0�ł���(�[)���[�}�����l�̂͋Ǐ��I�ɕ��R��Ԃɓ��^�ł���B�܂��A���̔핢��Ԃ͕��R��ԂƓ��^�ł���B >>253
�u�ށv�Ƃ͉��̂��ƂȂ낤����
> �u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v
�u���Ƃ��Əd�͂͂Ȃ��v�Ȃ�Ă��Ƃ͈�،����ĂȂ��B�u�^�̏d�͂͂Ȃ��v�Ƃ͌����邪�B
> �������̌������̗p����Ƒ��I�ɑł������邱�Ƃ��O��ƂȂ��Ă���̂Łu���������v�ŏd�͂��������ƂɂȂ�
��l�ȏd�͏�Ȃ���I�ɏ�����A�ƌ����Ă�B���R��l�łȂ��i�^�̏d�͂�����Ƃ��j�Ȃ�Ǐ��I�ɂ��������Ȃ��B
���I�ɏ�����ꍇ�͑��I�ɏ�����ƌ����Ă邾���B
> �����Ă��̏d�͂������ꂽ���E���{���̐��E�炵��
�u�{���̐��E�v�Ȃ�Ăǂ��ɂ������ĂȂ����v���Ă����Ȃ���B >>252
���q���v(���i�q���v�����q���v�̈��j����ɂ��Ă���u���q�̐U�����v�����q���u���u���ƐU���^�����Ă��Ă��̐U�����𑪂��Ă���Ǝv���Ă�̂��ȁH >>259
�������ނƂ́u3�v�̂��Ƃł͂���܂���
>>146�̂��Ƃł�
�u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�͈��p�Ȃ̂œ��R�ނ͂��������Ă��� >>256
�ނƂ́u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ɣ�������>>146�̂��Ƃł���
�ނ̒��ł͂��̗v�������݂������ƂŔF���̃Y����������
���͂��̗v�������Ă��鋳�ȏ����������Ƃ��Ȃ����̂ł�
���̗v���ł�>>4�̂悤�Ȑݒ�̓{�[�����Î~���ČZ���������Ă���{���̐��E�ɑ���������č��ꂽ���\�̐��E
������>>4�����̑���O�̖{���̐��E�ɖ߂��܂ł͋����Ƃ������Ƃ��낤
���̒��ł�>>4�̐ݒ�̂悤�Ȉ�l�d�͏�ɑ��݂���Z���܂��u���X�v�Ȃ̂� ���Z�����ł悭�o�Ă��鐢�E�i>>4�̂悤�ȁj�ɂ͌��X�d�͂��Ȃ������Ƃ�������
�v���Ƃ��č̗p����̂Ȃ�Γ��R�v�l�������炻�̑ΏۂƂȂ� >>262
���ȏ��̓�������͂��݂ɗ����ł��Ȃ��̂��낤���A���ݍӂ���������eman�ɏ����Ă���̂͏q�ׂ��ʂ�B
�������ɂ�芚�ݍӂ����\���Łu���Ƃ��Əd�͂͂Ȃ��v�Ƃ����Ă邪�A�d�͂��Ȃ��̂Ɠ��^�A�^�̏d�͂͂Ȃ��Ɠ��ӂ��B
�����Ă܂��u���^�v�Ɓu���\�v�̋�ʂ����Ă��炸�������Ă���̂͂��݈�l�B�i�u���\�v�Ƃ������t�͑��ɒN��l�g���Ă��Ȃ��j
�����������ݖ{�l�����^�Ǝv���Ă��邩��A���X�Ƌ^���d�͂�t�������Ė������ς����Ǝv�����B ���Ȃ݂ɓ��������̒m���������Ă������^�ƌ�����̂ŁA
���ꑊ�Θ_�̘g���ł�>>4�̂悤�ɏ���ɋ^���d�͂�t����������Ƃ��͂�ʖ��ɂȂ��Ă��܂��B
�o�q�̃p���h�b�N�X�́A���S�ɓ��ꑊ�Θ_�̘g���Ő����ł���̂͂���܂ŊF���������Ă����Ƃ���B
���āA����ɋ^���d�͂Ƃ����T�O��������ĉ��ς���>>4�����̂܂ܓ��ꑊ�Θ_�̘g���ł͐����ł��Ȃ��̂��A�܂�������܂��Ƃ������b�B >>4�͂��������p���h�b�N�X�ɂȂ��ĂȂ���ȁB
�u�Z���猩�ă{�[���̎��v���x���v�Ɨ\�z�ł���v�f(�����Ƃ�����Ƃ�)�������Ȃ��B >>265
>�o�q�̃p���h�b�N�X�́A���S�ɓ��ꑊ�Θ_�̘g���Ő����ł���
���ʂ܂Łh���S�h������̂�
���W�̕ϊ��Q�̊T�O�������ł��Ȃ��l���A�Q�̌��������Ȃ���Εs���S���B
�V�˃A�C���V���^�C���͒����ɓ��ꑊ�Θ_�̕s���S���ɋC�Â��āA
���S�Ȉ�ʑ��Θ_�̍\�z���J�n�����̂���B >>267
���ꑊ�Θ_�̘g���ł͑o�q�̃p���h�b�N�X������ł����A�o�q�̃p���h�b�N�X��F�߂邵���Ȃ��Ȃ�A
���ꑊ�Θ_�͖��������Ă���A�܂�Ԉ���Ă���Ƃ������ƂɂȂ�B
�����̂Ƃ�����ǂ��l���Ă�H ��
��̗ʎq�_�Ƃ��ǂ������
���ꑊ�Θ_�̏�ɍ\�z���Ă���ǂ���
>>269
�L�~�͔]���Â�ł܂��Ă�̂�
���ꑊ�Θ_�̍��W�ϊ��͊����n���m�̃��[�����c�ϊ��������A
�Q�̌��������Ă���B�܂�A���ꑊ�Θ_�ɓ��������������B
�o�q�̃p���h�b�N�X�̓��ꑊ�Θ_�ɂ��������ł�
���n���烍�[�����c�ϊ��ł��Ȃ��A�Q�̌�������݂�Εs���S�ȉ������ɂȂ�B >>271
��ʑ��Θ_�̗ʎq�_�͌��݂����������B
�����̕��������ł�CREN�����탌�x���ł��f���q���m�̏d�͍�p�͖����ł��邾���B CERN�̓u���b�N�z�[���̐������ړI�ł���
>>273
���w�I�ɖ������ȏ�̗ʎq�_�̃��f�������݂��܂��� >>273
�������Ȃ����̘b�����Ă���̂Ɉ�ʑ��Θ_��g�ݍ���Ō����ƍ���Ȃ��Ƃ����悤�ȑS�R�ʂ̂��Ƃ������Ă���̂͂Ȃ� >>275
>���w�I�ɖ������ȏ�̗ʎq�_�̃��f��
���̕���̐��w�҂��������A�����w�҂͖��������������܂ŋC�ɂ��Ȃ��B
>>276
�ʎq�_�̓��ꗝ�_���������Ă镨���w�҂͈�ʑ��Θ_�ɑΉ����Ȃ��Ɩ�������
�ƍl���Ă�B >>277
����Ȃӂ��ɂ͍l���Ă��Ȃ����ǂ�
��̗ʎq�_�̌����Ȓ莮������������Ă��邵�A�~���j�A���v���u�����������O��ɒ�`����Ă��邭�炢��
�����A�ЂƂł��������Ȃ��̂������Ŕ��_�ɂȂ��Ă��������͗����ł��Ȃ���ł����H >>277
����������������ƍl���Ă�����āA�����̂Ȃ����̂����݂��Ă�����Č����Ă��ł����ǂ�
�ԓ��Ƃ��ĈӖ��s���ł� >>278
�������Ȑ��w�I���_�͗��_�̉�㈂��疳�������ؖ��ł��Ȃ��B
�Q�[�e���̕s���S���藝
�A�[�@�I�ɏؖ����邵���Ȃ��A�����w�ł͎��������w���K�v�s���Ƃ������ƁB >>280
�����ɂ��Ă��閳�������͐��w�̌n���g�̖��������ł͂Ȃ��A���̏�Œ�`����镨�����_�̖��������Ȃ�ł���
������ؖ����邱�Ƃ͂ł��܂��ˁA�m���Ă錾�t��K���Ɏg��Ȃ�����������Ǝv���܂� >>281
>�������_�̖��������Ȃ�ł���
�I�}�G�͂��̈Ӗ��𑼐l�ɂ�����悤�ɐ������Ă���ɂ���
>�K���Ɏg��Ȃ�����������Ǝv���܂�
�u�[������ >>282
��̗��_�̖��������Ƃ�(���ϕ��Ȃǂ̖������������肵�����)�A��ԋ��(�q���x���g���)�ƍ�p�f����̓I�ɍ\���ł��Ă��̐ς��L���ɂȂ肩���[�����c�Ώ̐��Ȃǂ̗v���������Ƃ�
���R��͒m���Ă܂���ˁA���ꂪ���ɊȒP�Ŏ����ȗ�Ȃ�ł����ǂ�
self consistent qft �łł����ׂĂ݂��炢���Ǝv�����ǂ�
���R���ꑊ�Θ_�͖������Ȃ����Ƃ��O���A����Ȃ��Ƃ͎�����������ɂ���Ȃ�Ȃ�����
�ŁA�Q�[�f���̒藝�Ƃ����̘b�ɖ��Ӗ��Ȃ��̂������o���ė��āA�����������̔ے�����邱�̂��Ƃ肪�S�����Ӗ��Ȃ��
�������Ă��Ȃ����Ƃ������o���Ă��邩�炻���Ȃ��ł��� >>283
>���R���ꑊ�Θ_�͖������Ȃ����Ƃ��O��
�L�~�̃��X���͂��̂悤�ȑO������g�ݍ��킹���������낪
�����Ȃ�h�������_�̖��������h�Ƃ������Ă����̒N���p�X���邾���B
�܂�
�L�~�͕s���S���藝�͐��w���肾�Ɗ��Ⴂ���Ă�̂��H
��{�I�ȕ������_�Ȃ�Θ_���I�Ɍ���������Ă邩��A
�_���\���Ȃ�Q�[�e���̕s���S���藝�����R���藧�B
�܂�A���_�̖��������͏ؖ��ł��Ȃ��B >>284
���[�ސ��w�I�ɖ������Ƃ����ƌ����n�Ƃ��āA�Ǝ��ꂩ�˂Ȃ��̂Ŗ��ł�������
����mathematical consistency�Ƃ����̂͏�̗��_�ɑ��āA���w�I�Ɍ����ł���Ƃ����Ӗ��Ŏg����ł���A���ۂɘ_���Ȃǂ̒��ł�
�Q�[�f���̒藝�ŏo�Ă���_���I���������Ƃ͕ʕ��ł�
���p���m��Ȃ��l�ɑ��ĕs�e�ł�����
�܂��A���w�I�Ɍ����ł���A�Ƃ����Ӗ����Ǝv���Ă������� �u�Ȋw���_�̔��؉\���v�Ɓu�Q�[�e���̕s���S���藝�v�͐������Ă���
���؉\�����Ȋw�I��{�����ƌ��Ȃ��A�Ȋw�Ɣ�Ȋw�̋�ʂɗL���Ȏ�i�B
>>270
�܂�N�́A���ꑊ�Θ_�͊Ԉ���Ă���ƍl���Ă���ˁH >>272
�o�q�̃p���h�b�N�X�͓��ꑊ�Θ_�̃p���h�b�N�X�ł͂Ȃ��Ƃ������Ƃ��ȁH >>285
�������Ɩ��������͒��ڊW�Ȃ��B
���w�I�Ɍ����̕������_�Ƃ̔�r�E�]�����e�ՂɂȂ邾���B >>261
> �������ނƂ́u3�v�̂��Ƃł͂���܂���
> >>146�̂��Ƃł�
���������B���Ⴂ���Ă��܂� >>288
�܂������̂�
>�o�q�̃p���h�b�N�X
���w�̉��K���ł�����ȉ������ƈ�ʓI�ȉ����������邪
����ȉ����������ł͉����Ȃ������i��������͓̂�����j��ʓI�ȉ��������Ɖ�����B
���� >>272
>�Q�̌�������݂�Εs���S�ȉ������ɂȂ�B
�悭�킩���̂����A�Q�̌�������݂Ȃ��Ⴂ���̂ł́H
����Ƃ��������_�͂��ׂ��炭�Q�̌�������݂Ȃ��Ⴂ���Ȃ��Ƃ���Ă���́H >>291
�ł��ȒP�Ɍ����������
���ꑊ�Θ_�ł́i�o�q�́j�p���h�b�N�X�����ɂȂ邪
��ʑ��Θ_�ł́i�������Ă�j�ŏ�����p���h�b�N�X�ɂȂ�Ȃ��B >>292
>�������_�͂��ׂ��炭�Q�̌�������݂Ȃ��Ⴂ���Ȃ�
���̂Ƃ���
�Q���Ȃ��Ɖ����Z���揜�Z���g���Ȃ���B >>291
�v����ɃA�z�͈�ʑ��Θ_�Ő������Ȃ��Ɖ������C�����Ȃ����Ęb����H
�o�q�̃p���h�b�N�X�͓��ꑊ�Θ_�̃p���h�b�N�X�ł�����ꑊ�Θ_�ʼn�����A�Ƃ����̂������B >>289
���₾����ʕ����Č����Ă܂����c
�����K���I�ɓ�������g�����Ƃ����邩���₱�������A���ʂ͒ʂ�����ǂ� >>272
������悭�������X���[���Ă����A��ʍ��W�ϊ��͌Q���Ȃ����ǂ� ���̏������݂���ǂ�v���邗������
>>295
�A���L���f�X�͓���ȋ��ϖ@�Ő}�`�̖ʐς��v�Z������
�j���[�g���́u���ϕ��̊�{�藝�v�i�t���Z�j�����Ă����A�ŒN�ł��v�Z�ł���B
�A�C���V���^�C���̈�ʑ��Θ_�����l�A�}�l�ł����ʂ܂ŕ�����Η����ł���B >>272
> ���ꑊ�Θ_�̍��W�ϊ��͊����n���m�̃��[�����c�ϊ��������A
���ق��B���Ⴀ�j���[�g���͊w�̍��W�ϊ��̓K�����C�ϊ��������B
���܂��̒��ł͍��Z�����Ŕ��n��ɍ��W�n���g���͕̂s���S�ȉ��������Ă��Ƃ��B >>295
> �v����ɃA�z�͈�ʑ��Θ_�Ő������Ȃ��Ɖ������C�����Ȃ����Ęb����H
����ȁB�@�ł����ۂ͉����Ă�킯�ł��Ȃ��āA
�u���ꑊ�Θ_�ʼn������悭�킩��炫���Ƃ���͉����Ȃ��낤�A
�ł���ʑ��Θ_�͖��\�ۂ�����A�ǂ�Ȃ̂ł�������͂�����Ȃ��̂����i��̓I�ɂ͂킩��ǁj�v���Ęb�Ǝv���B >>272
> �Q�̌��������Ă���B�܂�A���ꑊ�Θ_�ɓ��������������B
����͒P�Ƀ��[�����c�ϊ������[�����c�Q(���邢�̓|�A���J���Q)���Ȃ��ƌ����Ă邾���ŁA
����ȊO�̍��W�n���g���Ă͂����Ȃ��Ƃ����_���ɂ͂Ȃ�Ȃ��B
> �o�q�̃p���h�b�N�X�̓��ꑊ�Θ_�ɂ��������ł�
> ���n���烍�[�����c�ϊ��ł��Ȃ��A�Q�̌�������݂�Εs���S�ȉ������ɂȂ�B
�g���b�ɂȂ邪�A���[�N���b�h���ʂ̊w���l����Ƃ��ɁA�������W���m�̕ϊ��͒����Q���Ȃ����A
����͒������W�ȊO�̍��W�n�i�ɍ��W�Ȃǁj���g���Ȃ����Ƃ͈Ӗ����Ȃ��B ���ꑊ�Θ_�̍��W�ϊ��̓��[�����c�ϊ��������Ƃ������o���悤�ȃA�z�ۏo���̑���ł��A
������܂��̂��ƂJ�ɕԂ��̂����炢��ˁB
�ق�܊��S����
�����������������番����Ȃ��ĕԂ��Ȃ�������c
���[�����c���k�͂���Ȃ����s�v�ȑ��݁B
�}���ɂ���đ��x���ς�邵�ʑ��𑵂����R�q�[�����X�Ȍ��Ō������z���鑬�x���o���Ă���B
���̎����猾���邱�Ƃ͌��͔}�̂�ʂ��đ��x�����܂�Ƃ������Ƃ��B�܂��}�̒��̌������x���Č��̋O�Ղ��o�����ۂ����邵�A
���Θ_�͋��\�ɂ����߂��Ȃ��B
���łɌ����Əd�͔g���o�͋���ȋ�������ł���B���������㉽���i�W���Ă��Ȃ�
>>264
����u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�͈��p�Ȃ�ł�
�������l�d�͂̂��鐢�E�͖{�����̐��E�ɂ͏d�͂��Ȃ��炵���̂�
���͂���ȗv�����̗p�������ȏ����������Ƃ��Ȃ����ǂ���炠��炵��
���Ȃ݂ɉ��������Ɠǂ͓̂��R�����_�E���炢�Ō�͕K�v�ӏ��E�������œǂ��
�v�l�����ł���ΏۂɂȂ�킯������l�d�͂Ń{�[���𓊂���Z�͖{���Z���������Ă���̂� >>265
���₾���炻�ꂪ���O�Ƃ̔F���̃Y��
�u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����v��������Ȃ�m����>>4�͖{���{�[�����Î~���ČZ���������Ă��鐢�E�������
������>>4�͂��̐��E�ɑ�����{���č��ꂽ���E�ɂȂ���
�������̊w��ł������ȏ��ł͂��̗v���͂Ȃ������̂ł�
���̗v�����̗p���Ă��鋳�ȏ���m�肽���� >>266
�o�q�̃p���h�b�N�X�̓��@�͓����Ă鎞�v�͒x���Ƃ������Ƃ���H
��2���v������ƌ݂��̎��_�ł݂͌��ɒx��Ă�̂ł͂Ȃ����H�Ƃ����̂����
�ł����ۂɂ͂����ƍl�@����Ή��������킯��
�Z���猩��ΐV�����̎��v���{�[���̎��v���x��邾�낤�ƂȂ� �v����Ɉ�l�d�͂�����>>4�̐��E�͌��X�̈�l�d�͂̂Ȃ����E�ɑ�����{���č��ꂽ���E
�����������ƂȂ킯��
���������̊w��ł������ΐ����_�ł�>>4�̐��E���܂����X�̐��E�Ȃ̂�
�����萳�m�ɂ͌��X�̐��E�Ȃ�ĊT�O���Ȃ��ƌ����ׂ��Ȃ̂�
������܂��A�C���V���^�C���������̉��̈�ɉ߂��Ȃ����� >>306
>����u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v
�d�͂͂Ȃ��A�̒�`���ɂ߂ĞB�����Ǝv���܂�
>�������l�d�͂̂��鐢�E�͖{�����̐��E�ɂ͏d�͂��Ȃ��炵���̂�
��l�d�͂̒�`�����X�B���ł��A��`�ɂ���Ă͈�l�d�͂����I�ɑł�������Ƃ͌���܂���
���ʂɉ��߂����
�d�͂͂Ȃ����ȗ���0�ł���
��l�d�́���ʓI����Ƃ��̏�̍��W�n�ɂ����Ĉ�l�Ȋ����͂������Ă������
�ł����̂��ȁH�Ȃ�ɂ���u�d�͂�����v�Ƃ������t�̈Ӗ�����т��Ă��炸�A�c�_�̑O���藧���Ă��Ȃ� ��悭�悭�l����Ɠ��^�Ɠ��ӂ��Ă̂��Y���Ă邾��
�d�͂��Ȃ��̂Ɠ��^�Ȃ�t�Ɉ�l�d�͂�����̂Ɠ��^��������
����ň�l�d�͐��E�Ɍ��X�d�͂��Ȃ��̂Ȃ疳�d�͐��E�Ɍ��X��l�d�͂�����ƌ����Ȃ��i�����������ɂƂ��Ă͌��X�Ƃ����T�O���̂ɋ^�₪���邪�j
����������Ȃ猋�nj��X��>>4�̐��E������
�����牴�̗���ł͓��^�Ƃ����̂͐����������X�]�X�͓I�O��
�d�͂��Ȃ��̂Ɠ��^�������X�d�͂��Ȃ����͑S���̕ʖ�� >>307
1.���ꑊ�Θ_�ʼn����x�n�������Ɗ�����(�d�͂Ɖ��߂��邱�Ƃ�����)��������
2.���̊����͂̂���n�͋Ȃ���������̓K���ȐÎ~�n��(�Ǐ��I��)�����ł���
3.���������ē��ꑊ�Θ_�ɂ����ĉ����x�n�������ɂ͋Ȃ��������K�v�ł���
�咣���������Ƃ͂���ł����̂��ȁH2����3�͔�Ă��邪
�ق�Ƃɉ��������������킩��Ȃ��̂ŁA������Ƙ_���X�e�b�v���ɂ����咣���܂Ƃ߂������ǂ��� �u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v
���x�������悤�ɂ��ꂪ�F���̃Y���̃L��������
���^�Ɠ��ӂƌ���������ł��̐��E�͌��X��l�d�͂�����Ƃ͂Ȃ�Ȃ��炵��
���̌��X�]�X�Ƃ����T�O�͉��̊w��ł������ȏ��ł͗v���Ƃ��č̗p����ĂȂ�����
>>4�͌��X�d�͂��Ȃ��{�[�����Î~���ČZ���������Ă��鐢�E������
�����炻�̗v����F�߂�Ȃ�>>4�͊��Ɍ��X�̏d�͂̂Ȃ����E�ɓ��������𗘗p�������삪���������E�Ƃ������Ƃ��낤
���ꂪ���Ɣނ̔F���̃Y����[�I�ɕ\���Ă� >>313
�������悤�ɓ������ƌ����˂�B
> ���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ�
����͕��R�Ȏ���A�ȗ�0�A�^�̏d�͂͂Ȃ��AEMA�̌��tN�Ȃ�u�����ɂ���ċ[���I�ȏd�͂������Ă����Ƃ��Ă�,����͋Ȃ����ĂȂǂ��Ȃ��Ƃ������Ƃ�.����͒N���猩�Ă��Ȃ����Ă��Ȃ��v
�o�q�̃p���h�b�N�X�̐��E�͂��Ƃ��Əd�͂Ȃlj��肵�Ă��Ȃ��B
��l�d�͂������Ă������Ƃ����̂́A�����܂œ���������m���Ă闧��ł��������Ȃ����ƁB
�v�l�����Ə̂��āA����ɓ����������g���ďd�͂�t��������>>4�͑o�q�̃p���h�b�N�X�Ƃ͂܂������ʂ̖��B
�d�͂Ƃ����T�O����ꂽ����ꑊ�Θ_�ʼn����Ȃ��b�ɂȂ�͓̂�����O�B
�ǂ�ȋ��{�{�ɂ����ꑊ�Θ_�̘b�Ƃ��ďЉ��Ă�o�q�̃p���h�b�N�X�B
���݂͂���ɏd�͂Ƃ����u�T�O�v��t�������ď���ɖ������ς��Ă���F�����Ȃ��B
���ꂪ���݂̔F���̂��ꂾ�B
���z�d�͂�����̂Əd�͂��Ȃ��̂ǂ������{���̐��E���Ƃ����b�����Ă���̂ł͂Ȃ��B
�ǂ��������������ǁA���ꑊ�Θ_�̘b��Ȃ���d�͂Ƃ����T�O������ɓ����ȂƂ����b���B >>308
>�o�q�̃p���h�b�N�X�̓��@�͓����Ă鎞�v�͒x���Ƃ������Ƃ���H
�p���h�b�N�X�̌��_�́A��̊����n�̊ԂŌ݂��̎��v���x���Ƃ������Ƃ���B
�u�����n�v�����������āA���ł�����ł�����̎��v���x���Ȃ�čl���邩��l�@�����������Ȃ�B >>315
>�p���h�b�N�X�̌��_�́A��̊����n�̊ԂŌ݂��̎��v���x���Ƃ������Ƃ���B
����ȁA�f�l�����ꑊ�Θ_�̋L�����ȂǂŒm���āh��������h�p���h�b�N�X�B
�^�����Ă鑊��̎��Ԃ��x���̂����������i�䖝���āj�A������̗��R��
�`����a�̊ϑ����ԂƂa����`�̊ϑ����Ԃ��_���I�Ɉ�v���Ȃ��Ƃ��������B
�Ⴆ��
�`����a�̊ϑ��ł`�Q�b�a�P�b�Ȃ�A�a����`�̊ϑ��ł`�Q�b�a�P�b�łȂ���Ȃ�Ȃ��B
���ꑊ�Θ_�̃��[�����c�ϊ��ł́A�a����`�̊ϑ��ł`�P�b�a�Q�b�ɂȂ邩��
�h��������h�Ǝv���B
�Ƃ��낪�o�q�̃p���h�b�N�X�ł�
�`�i��j����a�i�Z�j�̊ϑ��ł`�Q�b�a�P�b�Ȃ�A�a����`�̊ϑ��ł`�Q�b�a�P�b�ɂȂ�B
�f�l�ɂ͘_���I�Ɉ�v���Ă邩��A���ꑊ�Θ_�́h�������Ȃ��h�i���Ԓx��͔F�߂�j�Ǝv���B
�����
���ꑊ�Θ_�̃��[�����c�ϊ��܂ʼn���������҂̏ꍇ�́A���[�����c�ϊ��ł�
�`����a�̊ϑ��ł`�Q�b�a�P�b�Ȃ�A�a����`�̊ϑ��ł`�P�b�a�Q�b�ɂȂ�͂����B�i�����ł͂Ȃ��j
�Ƃ��낪�o�q�̃p���h�b�N�X�ł�
�`�i��j����a�i�Z�j�̊ϑ��ł`�Q�b�a�P�b�Ȃ�A�a����`�̊ϑ��ł`�Q�b�a�P�b�ɂȂ�B
���������ă��[�����c�ϊ��i�Q�j�̊T�O����_���I�Ɂh�������Ă���h�B�p���h�b�N�X���Ǝv���B
�܂�A�o�q�̃p���h�b�N�X�͓��ꑊ�Θ_�̓���҂��˘f���p���h�b�N�ƌ�����B
���l��
��ʑ��Θ_�܂ŗ����ł���A���������p���h�b�N�X�Ȃǖ������Ƃ����邾�낤�B ����A���[�����c�ϊ���������_�őo�q�̃p���h�b�N�X���킩������炻�����[�����c�ϊ��킩���Ăˁ[��B
�o�q�̃p���h�b�N�X�̍l�����Ȃ�ċ��{�Ƃ��ďЉ�����e���B
���ꑊ�Θ_���Ȃɂ����I�Ɋw���Ƃ̂Ȃ����Z�����}�����Ŗ{��āA
�Z���猩����̎��Ԃɂ��Ď����ōl���č�}���Ă݂đ��Θ_�킩����������Ɗ�Ԓ��x�̖��B
>>318
>���ꑊ�Θ_���Ȃɂ����I�Ɋw���Ƃ̂Ȃ����Z�����}�����Ŗ{��āA
>�E�E�E���Θ_�킩����������Ɗ��
�h�f�l�́u�^�����Ă郍�P�b�g�̎��Ԃ��x���v�����F�߂��
�o�q�̃p���h�b�N�X�ɖ������Ȃ��B
�Ə���Ɏv�����ށB
����������A>>316 �̂悤�Ɂu�݂��Ɏ��Ԃ��x���ق����������v
�̂܂܂Ől�����I����B >>319
����Ȃ��ƂȂ��A���Θ_�ɋ������������n�̍��Z���Ȃ�Z���猩����̎��ԂƂ������_�ł��l���Ă݂�B
�����āA�Z���܂�Ԃ����ɋ}���ɒ�̎��Ԃ��i�ނ��Ă��ƂɂȂ�A������d�͂ƍl�������ɍs���قǎ��Ԃ̗��ꂪ�����Ȃ�B
����莮������Έ�ʑ��Θ_�ɂȂ��Ȃ��̂��H
���Z���ň�ʑ��Θ_�𗝉�����Ƃ͂Ђ���Ƃ��ĉ��V�˂Ȃ̂ł́c�Ɗ��Ⴂ����Ƃ���܂ł��ʏ�^�]�B >>320
�܂�����͎��ۃA�C���V���^�C�����l�������Ƃ�����
�����ł����܂ōl����ꂽ�猤���E�ɂ͂Ȃ�邾�낤�A������x���w���ł���� ���Θ_�̌v�Z�̎���������Ă�������
�Î~���Ă�A���猩�ĉE������B����A��������C����l�Ƃ�������80%��t�b�Ԑi�Ƃ���
B����̐i�����Ǝ��Ԃ�C���猩���Ƃ��̌v�Z�ɂ��Ăł�
����c=1�ʼnE�������Ƃ���A���猩��B�����t�b�Ԃ�8t/10�i���A�����C����̑��Α��x��-8t/10������
������
(164/100)t��(6/10)
���Ԃ�
(16/10)t��(6/10)
������C���猩��B����̑��x��
160/164
�Ƃ������Ƃł����Ă܂���
>>321
���������������Ⴞ�߂������ʑ��ΐ����_�\�z������ >>324
���Z���ł��Ȃ��̂ɁA���܂��ɂ���Ȃ��ƌ����Ă�Ƃ��� >>316
���̂悤�ȊȒP�Ȗ��ɕς���������œ��ꑊ�Θ_�ł͉����Ȃ��B
�P�D2�̃��P�b�gA,B������ʒu����o�����Ȑ��^���Ō��̈ʒu�ɖ߂�Ƒz�肵
�@�@A,B�͉^������̊ϑ�������瑊��̎��Ԍo�߂��v�Z����B
�Q�D2�̐l�H�q��A,B�����d�͏�ԂňقȂ����O����`���Č��̈ʒu�ɖ߂�
�@�@A,B�͉^������̊ϑ�������瑊��̎��Ԍo�߂��v�Z����B >>327
�ŗL���ԉ��ĉ���͂����Ȃ� >>325
�����Ȃ�W�Ȃ����ƌ���Ȃ��� >>332
�p���h�b�N�X���d�͏�̒��ɂ���Z���l���d�͏�ɂ��Z�̎��Ԃ̒x��Ő�������Ƃ����̂́A�A�C���V���^�C�������ۂɍl���Ă��˂Ƃ����b ����ቴ��}�l�ł��l�������Ƃ��A�A�C���V���^�C�����l���Ȃ��킯�Ȃ����낤
����������͂�����x�[�֏��Ŋw��Ō�ǂ��Ŏv�����ɉ߂��Ȃ���
>>333
�A�C���V���^�C��������ȍl�@�����Ȃ�ĕ���������H https://arxiv.org/pdf/1807.07015.pdf
��̘_����ʂ�ڂ�ʂ��Ă݂�
���ʗ��Ȃǂ̖�肪�N���Ȃ����߂ɂ�(�d��)��̗ʎq��炬�Ɨʎq�I�ȕ��˂��l������K�v������Ƃ͂Ȃ��Ȃ�����
�ق�Ƃ��ɌÓT�I�Ɉ����Ė�肪�N����̂��͏��������ׂĂ݂Ȃ��� >>335
A. Einstein, �gDialog über Einwände gegen die Relativitätstheorie,�h Naturwissenschaften 6, 697–702 (1918).
�ɂ���炵�� >>337
�����������������Ɠǂ�ł݂邩

�u�o�q�̃p���h�b�N�X�Ɉ�ʑ��Θ_���K�v�Ǝv���̂͊ԈႢ�v�Ă̂�������邽�߂�
�ʐM���Ȃ��炾�Ƃǂ��Ȃ邩�������Ă��͉̂��̖{���������ȁ[�H
>>327
���̖�肪���ꑊ�Θ_�ʼn����Ȃ��Ƃ������Ƃ́A���̖��̂悤�ȏɂ����āA���ꑊ�Θ_��
�u�^�����Ă���Z���猩����Î~���Ă����̎��v���x���v�Ƃ͌����ĂȂ����Ă��Ƃ��B
������o���h�b�N�X���̂��������Ȃ��B
��������^�����p���h�b�N�X�̉������@�̂ЂƂ��B
�p���h�b�N�X����������̂ɁA�킴�킴����Ȍv�Z�ɂ܂ŗ�������K�v�ȂǂȂ��B >>341
�p���h�b�N�X���������Ȃ��łȂ�
���ꑊ�Θ_���Ԉ���Ă��邩�炾�� �p���h�b�N�X���������Ȃ��Ƃ��A���ꑊ�Θ_���ǂ��Ƃ��ȑO�ɁA�����v�Z���������̂��������ς��ǂł��Ȃ�
�܂����œ�����������ɒP�ꂾ���ς��Ă����������Ă�Ǝv�������A
�P�������ĂQ�������Ȃ����Ęb�Ȃ̂��ƋC�Â��܂łɂP���Ԃ��炢��v�����ȁB
�ŁA�����Ⴄ�̂��l������A�l�H�q�����ĒP�ꂪ�L�[���[�h���B
���d�͂��ď����Ă��邯�ǂ���̓t�F�C�N�Ől�H�q��������f���̏d�͏�Ŏ���i���R�����j���Ă�̂��ȂƂЂ�߂����B
�d�͏�̖�肾������ꑊ�Θ_�͈̔͊O�Ȃ̂͂�����܂��Ƃ���������_�������B
�^������̊ϑ�������瑊��̎��Ԍo�߂��v�Z����̈Ӗ����܂���ǂł��Ȃ��B
�ϑ������������Ɍ��̓`�B���x����t�Z���Ĉʒu�����߂���Ęb�����v�������A��������܂�Ӗ��͂Ȃ��낤�B
>>342
�v�Z�Ɋ�Â��Ȃ��咣�̐ӔC�܂ŗ��_�ɕ��킹��Ȃ�B
���ꂾ����}���K��[�֏������ǂ߂Ȃ��z�̓_���Ȃ�B >>314
�������Ƃ���������Ⴀ�u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����v���̗L�����F���̃Y���̌����������̂�����d���Ȃ�
���̗v��������Ȃ�>>4�͂��̌��X�d�͂̂Ȃ����E�ɑ�����{���č��ꂽ���E�ɂȂ�i�܂�{�[�����Î~���ČZ���������Ă��鐢�E�����X�Ȃ́j
���ɂ͂��̗v�����Ȃ������̂Ō��X�]�X�Ƃ����T�O�͏o�Ă��Ȃ�
�������F���̃Y���Ȃ킯
��ł������������̗���ł͈�l�d�͂�����Ƃ��͏d�͂��Ȃ��̂Ɠ��^�͎x�����邪���X�͏d�͂̂Ȃ����E�Ƃ����̂͂Ȃ�
���ꂪ���ӂƌ���ꂽ���Ȃ猳�X��l�d�͂�����������������킯�ł����>>4�̐ݒ�����X�ɂȂ��Ă��܂�
�ł���������Ȃ��炵���������ς萳�����͓��ӂł͂Ȃ��낤
���ǁu���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����v���̗L���Ɏ������� �܂��������������ƌ����Ă�悗
��قlj������Ė�����s��Ȃ���C�����܂��悤�ɂȂ��Ă낤�ȁB
���Ȃ����Ă�̂͘_�O����
������������͐����X�s�����Ă��邩�猈�߂�ꂽ�T�O�ł����āA�m���߂�ꂽ���̂ł͂Ȃ�
�������Ă邩�킩���̂ŁA�������������̊��z�������ɂ��Ȃ��Ă���
>>350
����͋Ȃ����Ă���ƌ����Ȃ�A�؋��������Ă��� >>351
�N�����O�ɑ��Ď���͋Ȃ����Ă���Ȃ�Ęb�͂��ĂȂ��Ǝv�����H
�������Ă邩�킩���̂ł������������̊��z�������ɂ��Ȃ��Ă����Ƃ����b�������Ă��Ȃ� �n�������ʂ����Đl������炵�����ǁA
�m���Ɏʐ^����֊s���ۂ��̂͂킩�邯�NjȂ����Ă邩�ǂ������Ă킩��ˁ[���ȁB
�l�I�ɕ��炾�Ǝv����Ȃ�v���ł�����ˁB
>>351
�����͂̊w�I�\�����B
SR + ����������������ł��Ȃ������ϑ������S�����؋��B ���̖�������������͉̂F�����Ȃ����Ă邩��Ȃ̂ˁB���ɂȂ�܂���
�����͂̓j���[�g���d�͂Ő����ł��邪���̏d�͂�����͎̂��Ȃ����Ă��邩�炾�����
����͐������Ȃ�����
���_��������ǂ�������Ȃ��Ă���ɔ[���ł��邩�ǂ�������Ȃ��́H
�����̃X���b�h�^�C�g���ɕs���������Ă�́H
>>357
>�����͂̓j���[�g���d�͂Ő����ł���
�ȁH�Ȃ��ʑ��ΐ����_�͕K�v�Ȃ���ˁH ���܂��̐l���A���܂�Ď��ʂ܂Œ����͂̐������Ă邾�����Ă�Ȃ�v��ˁ[��ȁB
>>360
�������������ăj���[�g���͊w�Ŏg���Ă�B
�������������ԂɁA�����͂���ԂɊւ���Ă���Ă̂���ʑ��ΐ����_�B >>363
�|�G�������Ă�Ȃ�����A����ȈӐ}�̂킩����������Ȃ����Ȃ玮�Ŏ����Ă���B ���ǁu���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����v�����̗p���Ă���͋��ȏ��͒���Ȃ������Ȃ��c
>>364
�A�z�E�A�e�L�X�g�ǂ߂�B
���������x�̃x�N�g������=���[�}���e���\���~�Ԋu >>366
����ȃ|�G���̏����Ă��ꂪ���ΐ����_���Ɗ��ł�e�L�X�g�Ȃǒm��� >>368
���O���A�z�����炾��B>>366�̎��́�����̈��p�B
P.C.W.�f�C���B�X��(���c����)�u�d�͔g�̂Ȃ��v(��g����I��) �����܂������Ȗ{���o���ė����ȁB
>>370
�C�ɐH���̂Ȃ甽�_�����炢�� >>372
���̃T�C�g�����{����̈��p�����B�A�z�߂� >>365

Carroll, Sean M. (2004), Spacetime and Geometry: An Introduction to General Relativity, San Francisco: Addison-Wesley

Zee, Anthony. (2013), Einstein Gravity in a Nutshell, Princeton University Press
�����������ƌ���Ȃ��ł� >>373
�H
���{�̓��e�����p���邽�߂ɁA���̃T�C�g���g�킹�Ă��������������B >>369
�[�֏��Ŏ��Ɛ}�������āA���̓��e�ɂ��ĕM�҂Ȃ�̂��ݍӂ�������������̂͂킩�邪�A
�������Ȃ��ɂ��������R�s�y�������ĈӖ��̂Ȃ��|�G���ɂ����Ȃ�Ȃ�
�[�֏��蔲���Ă킩�����C�ɂȂ��ăh���炵�Ċ��ł�̂̓A�z���� >>375
���p�������Ă�̂ɈӖ��s��
>>376
���p���̗L���Ō��_���ς�邩�A�A�z ����Ȗ{�ǂ�ł�̂���c�ԈႢ�Ƃ͌�����S�Ҍ����̐����̂ɑ����s���m�ȓ��e�ɂȂ��Ă邼�A�����Ƃ܂Ƃ��Ȃ̓ǂ�
>>373
���p���̖{�̓��e���݂�Ȍ���Ȃ�����킴�킴�T���Ă��ċc�_�ł���悤�ɂ��Ă��ꂽ�̂ɂ��̕Ԃ��͑�������� >>378-379
�A�z���n�Q�U�炩���Ȃ�B
���̎���(�x�����q��)���n�����������B�����������A�n�������� >>380
����������ƐS�ɗ]�T����������H
���s���炢�N�ɂ����Ă��邳�B �ق�܁A�j���[�g�����炢�łƌ�������
>>365
�u�^�̏d�́v�͂Ȃ��Ƃ͌�����ˁB
�^�̏d�͂Ƃ����͍̂��W�ϊ��ő��I�ɏ������Ƃ��ł��Ȃ��d�͂̂��ƂȂ̂ŗv�̓g�[�g���W�[�����B
�i�O�ׂ̈Ɍ����Ă����Ɓu�^�̏d�́v�͉��̑���ł͂Ȃ��j >>365
�v������Ȃ��Č��ʂł́H���u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v ���c��ł�̂ł͂Ȃ��A�������c��ł�̂��B�V�˂ł����Ԃ����Ă����_�͂��ǂ蒅�����͓���B
�|�G���Ȃ�ď����������������A�������݂����Ȃ��ȁB�݂��Ƃ��˂���
�܂��[�֏��ǂނ̂͂������ǁA���Ж����킸�e�L�X�g�Ƃ������Ă���������Ă����Ƃ���ŃR���v���b�N�X���f����B
����܂���̂��R���v���b�N�X���Ǝv�����A�u�A�z���n�Q�U�炩���Ȃ�B�v�ŕs�o�ɂ����Ă��܂����̂�������Ɖ������B
>>390
�����Ȃ��āB ���n�����������Ȃ��̃e�L�X�g�ɏ����Ă�B ���̃e�L�X�g�ɏ����Ă�͂��Ȃ̂ɁA�₢�������ꂽ�Ă�ނɂ�܂ꂸ�������̂͌[�֏��B
���������Ƃ��₼w
>>392
�O�O��������ȁB��w�̍u�`�����Ƃ�������ł��q�b�g����B���A���̒m���O�O��悤���Ȃ��������B
���{�ꍬ����̎��A�[�֏���������ĐҐ����˂Ń��X�����낤���A�m�������Ԃ�̔n�������ĎN����ĉ������낤�B ���h���Ă�����������邾���Ȃ���~�߂�Ηǂ��̂ɁB
���R�Ƃ��{���Ƃ��V���b�c�Ƃ��̖��O�͏o�Ă��Ȃ��́H
�[�֏��̎����l�b�g���āA�����Ƃ����{�������ĂȂ��؋������B
�X���^�C���Ԉ���Ă邱�Ƃ��ǂ�������X������
�i���ʒ��x�̒m�\�Ƃ��C������j���ΐ����_�𗝉�����̂͌����قǓ���Ȃ�
���������l�͂����������Θ_�đo�q�̃p���h�b�N�X���Ȃ̂��Ƃ��Ǝv���Ă�
>>394
����������Ȃ���
> ���R�Ƃ��{���Ƃ��V���b�c�Ƃ��̖��O�͏o�Ă��Ȃ��́H
����Ȃ̎����ĂĂ����n�����������킩������n�����낤���A���O��
> �[�֏��̎����l�b�g���āA�����Ƃ����{�������ĂȂ��؋������B
����A�ʓ|������B >>398
���͍���͂��߂đ��n������������m�������ǂ��A
���n�����������ɂ��ĉ����ł���A���n���������������Ă��邱�ƂɂȂ�H
���t�����m���Ăċ������Ε������Ă��邱�ƂɂȂ�Ȃ�Ă킯����Ȃ���H �Ȃ������Ă݂��炢�����ȁB
�q���O�����2���_�̋O�ՂƂ�
���n���������������ő��Θ_���������Ȃ�Č����z����H
>>400
�����͂��̃|�G�������n�����������̐������ƌ��������Ă���ŁB
> 363 ���O�F����k�ł��傤�H����������[sage] ���e���F2021/12/19(��) 23:43:27.71 ID:???
> >>360
> �������������ăj���[�g���͊w�Ŏg���Ă�B
> �������������ԂɁA�����͂���ԂɊւ���Ă���Ă̂���ʑ��ΐ����_�B >>405
�A�z�̂��O���A���n�����������ƃ|�A�\������������A�C���V���^�C�������������Ƃ�����Ă݂���H���߯ >>374
��H�����ɂ́u���I�ɑł�������Ȃ炻�̐��E�ɂ��Ƃ��Əd�͂͂Ȃ��v�Ƃ����v��������Ƃ͏�����ĂȂ����ǁH
���̃I���W�i�����߂�����̂��낤�� >>406
�|�G���t��
����������^�]�ł��� >>384
�ł��傤��
�^�̏d�͂Ƃ������t���g����ꍇ�͕��ʍL�`�̒����͂�����̂���`������g�[�g���W�[�Ɋׂ�
�ܘ_�����ɂ͌��X�d�͂�����/�Ȃ��Ƃ�����ȊT�O�͏o�Ă��Ȃ� >>407
1.���I�ɑł�������Ȃ�ȗ��̓[���ł���(�藝)
2.�d�͂Ƌȗ��͓������̂ł���(���p)�A�����ȗ����[���Ȃ�Ώd�͂͂Ȃ�
����� ��������50p�ӂ肩��ǂ߂����̂��Ƃ����ʂɏd�͂Ǝ���̘c�݂����т��Ă邾������
����>>411�̒ʂ��l�d�͂����ʂɓo�ꂵ�Ă��Łi�d��=�ȗ��Ȃ玩�Ȗ����Ɋׂ�j >>412
�ǂ������p���Ă邩��������A
�_���m�ɂ���悤��
���������������킩��܂��� >>413
50p�Ƃ�carroll�̖{�̂��Ƃ�
�Ȃ�Έ�l�d�͂̉ӏ����w�E���Ă��炢����
���̑O��ł͓��������̋c�_�̂��߂Ɂu�Ǐ��I�ȁv�����x�n�ƌ�������̏d�͂������Ă��邾���ő��I�Ȍn�͂قڏo�Ă��Ȃ� >>418
uniform grav �Ō��������낵��
�Ⴆ�X�N�V�����̐ԕ��Έڂ̉ӏ�
EEP�̐����ɂ���悤�ɔ��̒��̐l�͈�l����/�d�͂̋�ʂ������i���Ȃ��ƌ����Ă���
���X�d�͂�����/�Ȃ��ł͂Ȃ���ʂł��Ȃ�
������EEP�ɂ��ԕ��Έڂ̐����͂ǂ��炪���X�̐��E�Ƃ��o�Ă��Ȃ�
�P�Ɉ�l�d�͏�ł����̎��ۂ��N����Ə����Ă��� >>413
�u�����@�͎�����Ȃ������w�ŋL�q���A�d�͂��ȗ��̌���ƍl���邱�Ƃ��v
���̈ꕶ��ے肷��Ƃ������Ƃł����̂��ȁH >>419
�m���Ɍ��̕����ɂ͏�����Ă����
�ł���̂����炫����Ǝw�����Ă��炢����
����ɒT���������ǂ�����̂͂�낵���Ȃ� >>420
��ł������Ă�悤�ɒ��҂͂���ȋ����Ӗ��ŏd��=�ȗ��ƌ����ĂȂ��Ƃ������ꂾ��
��l�d�͏��F�߂Ă邵 >>421
���p���Ă����炻�̎��ӂ͓ǂ�ł�O��Řb���Ă��܂���
�C�����܂� >>422
�����Ӗ��Ō����ĂȂ��Ƃ͂܂��悭�킩��Ȃ���
�ł͒��҂͂ǂ������Ӗ��Ō����Ă�낤��
zee�̕������������A�������ア���Ȃ��A�B�����̂Ȃ������Ǝv�� >>419
>EEP�̐����ɂ���悤�ɔ��̒��̐l�͈�l����/�d�͂̋�ʂ������i���Ȃ��ƌ����Ă���
�Ǐ������n�ł͋�ʂł��Ȃ������B
�����͂̑��݂ȂǂŐ^�̏d�́i�ȗ����O�j�ƈ�l�d�́i�ȗ����O�j�͋�ʂł��邪
������ϑ�����ɂ͋Ǐ������n�ł͖��� ���ΐ����_���ė�������̓���l������
�Ǐ��ł͋Ȑ��ƒ����i�ڐ��j�̋�ʂ����Ȃ��̂Ɠ����B�L���͈͂������ʂ����B
�i���炩�ȁj�Ȑ��͋Ǐ��I�Ȓ������q���ł��������̂Ƃ��Ĉ�����B
���l�ɁA�Ȃ�����������Ǐ��ł͕��R�Ȏ���Ƃ��Ĉ����邱�Ƃ�ۏ���̂����������B
���̕��R�Ȏ���i�Ǐ������n�j�ł͏d�͂̂Ȃ����ꑊ�Θ_�����藧���Ƃ�v�����A
��͐ڑ��Ōq���Ă����Ȃ���������ł̐U�镑�����L�q�����B���ꂪ��ʑ��Θ_�B
�Ⴆ�Η��q�̋O���͋Ǐ������n�ł͖��d�͂����瓙�������^���B
������Ȃ���������Ɍq���ł����Α��n���ɂȂ�B���ꂪ�d�͏ꒆ�ł̗��q�̋O���ɑ��Ȃ�Ȃ��B
��ʑ��Θ_�̐����͂�₱�������v�z�͒P������
�����ǂ��l�͕�����₷�����������Ĕ[��
���������l�͕�����ɂ������������ė���s�\
>>425
>������ϑ�����ɂ͋Ǐ������n�ł͖���
�Ǐ������n�Ȃ�Č��z�ł��� �z������������Ȃł���킯���Ȃ�
���z�Ŏ~�܂��Ă�z�͖����̎�
�G�[�e����z�肷��Ώd�͂̓G�[�e���̘c�݂��琶���鈳�͂ƂȂ�B���������ꂾ���̂���
�G�[�e���̕�������ł��Ȃ��Ȃ��O����
>>424
��l�d�͏��F�߂Ă��邩���
���̘b�͊��ɏ�ł��Ă�̂łǂ��� >>425
��ʂɂ͂�������
���p��ǂ�ł��炦��ƕ����邯�Lj�l����/�d�̘͂b���o�Đԕ��Έڂ̘b�Ɍq�����Ă���
>>4���炻���Ȃ�� ���������̒��Ō�����Ǐ��I�ȏd�͂́A��l�d�͏�Ƃ͕ʂ̊T�O����
�������EEP�ň�l�d�̘͂b������̂��o�Ă��Ă����
���������Ȃ烌�X���炢�ǂ��Ă����
�܂��X�N�V���\�����l���������Ă��ꂽ��ŊO�삪���X�ǂ킸�ɂ��Ă���Ȃ��͎̂��ȐӔC��
�{�̘b���Ă�Ǝv�����瓂�˂ɂ܂�>>4���o�Ă��ă����^w
���� >>4 >>4�����˂� >>433
�܂��A�ǂ������Ӗ��Ō����Ă�̂��Ƃ�������̓����ɂ͂Ȃ��Ă��Ȃ�
��ɓ������Ȃ�����ɓ������떂�����̂͂�߂������ǂ�
��l�d�͏�Ƃ������t���o�Ă��镔���̎v�l�����̃Z�b�e�B���O�ł����\���ق��ɓK���Ȍ��t���L�邾�낤���H
���܂Ŏg���Ă����ȏセ�����������Ȃ��̂Ŏg���Ă���Ƃ��낪����A���̒���̏d�͏�(�j���[�g�����d�͂ɂ������x�Ɠǂ���)�Ƃ��������ɂ��ꂪ����Ă���
���܂ł̔F���Ɋ�Â��Ώd��(�ƌĂ�ł�������)�͑��݂��Ă��邪�A��ʑ��Θ_�I�����ɗ��Ă���͊����͂ɉ߂��Ȃ��Ƃ������t�̎g���������ǂݎ��邾�낤 >>433
������Ƃ킩��Ȃ������͔̂F�߂�Ƃ͂ǂ������Ӗ��Ȃ̂��Ƃ�������
���������������Ă���Ȃ��Ƃ킩��Ȃ��A���������s�\���Ɏv�� >>433
�d�͏�Ƃ������t(�������͂���ɔ����F��)�Ƃ����Ӗ��Ȃ̂��A��l�łȂ����̂����łȂ���l�Ȃ��̂��l���Ă���Ƃ����Ӗ��Ȃ̂� >>438
���₾���烌�X�ǂ����Č����Ă���
���ꂷ�点���Ɏ����̎v���ʂ�ɂ����悤�ƍl����̂͂�߂Ȃ���
��ʓI�ɏd�͎͂���̘c�݂Ƃ��������Œ��҂͋ȗ�0�ƂȂ�悤�ȏd�͏���F�߂Ă���
�ȗ�0�ł��d�͂�������
�ȗ�=�d�͂�����ȗ�0�Ȃ�d�͂͂Ȃ��ƂȂ�悤�ȈӖ��ł͂Ȃ��� ���҂͞B�����Ȃ���l�d�͏���l���Ă���
>>441
��l�d�͏�͋ȗ���0������Ƃ����Ӗ��łł��ˁA�킩��܂���
�ǂ��̃��X�ł�������Ă����̂������Ă��炢����
�����Ă�͂��l�d�͏�ȊO�̓K�Ȍ��t�����邩�H�̕����Ɋւ��Ă͖��������Ă���
�s�����������炾�낤���H
�������Ԃ��Ă��Ȃ�����b�̐i�߂悤���Ȃ� >>441
�ŁA�����Ӗ��Ō����Ă��Ȃ��Ȃ�ǂ������Ӗ��Ō����Ă���̂��Ƃ����₢�ɂ������Ă��炢����
���ꂪ�ł��Ȃ��Ȃ炱�̖{�͖����������e���܂�ł���Ƃ������ƂɂȂ邪�ǂ��̂��낤�� ��ʑ��Θ_����d�͏�Ǝ���͓����Ӗ�����
�d�C�ʂ�`����G�[�e��������ł�
����4�����ł�
�d�͂�5�����ł��B
�J���c�@�N���C�����_�ł͓d���I�ɓ��ꂳ��Ă���B
�����ɂ͌ŗL�U����������̂́A����������R��Ă��邩�炾��
>>444
>>413�ŏd��=�ȗ��Ȃ��l�d�͂������o���Ă�̂Ŏ��Ȗ����Ɋׂ�Ǝw�E���Ă���
�����炻��ȈӖ��ŏd��=�ȗ��ƌ����ĂȂ��Ƃ������Ƃ���
�ȗ�0�ƂȂ�悤�ȏd�͂�F�߂Ă���̂ň�l�d�͂Ƃ������t�͓K�Ȍ��t�ł����Ȃ��킯����
>>413�Ō����Ă���悤�Ɉ�ʓI�ɏd�͂�����̘c�݂ƌ��т��Ă邾�����낤��
�j���[�g���̏d�͗��_�ƈ���ăA�C���V���^�C���͏d�͂����̂��̂ƌ��т���
�����Ă������邱�ƂŎ�X�̖����𖾂��邱�Ƃ��o����
�i�ܘ_���R�Ȏ���ƂȂ�d�͏�҂͔F�߂Ă���j �J�닭���Ӗ��ŋȗ�=�d�͂��咣����Ȃ炻�̐l����l�d�͂Ƃ������t�ȊO��T���Ȃ��Ă͂Ȃ�Ȃ�
���̂Ȃ炻�̗��_�ł͈�l�d�͂͏d�͂łȂ��̂�����
���R�Ȏ���ƂȂ�悤�ȏd�͏��F�߂�Ȃ�ܘ_����Ȍ��t��T���K�v�͂Ȃ�
�P�Ɂi�L�`�́j�����͂����邩�Ƃ���������
>>438�ɂ��ƕ��R�Ȏ���ƂȂ�d�͏��F�߂Ȃ��l�́u�����́v�ƌĂԂׂ��Ƃ������ƂȂ̂���
�܂����̌��t���͓̂���݂�������̂��� >>449
�u���т��Ă��邾���v
�ł͂��̕����ǂ��ł����ˁA���т��Ă��邾���ł��傤��

>>452
����܂Ō����Ă����悤�Ɉ�ʘ_�Ƃ��ďd�͂�����̘c�݂ł���Ƃ����b���Ƃ�������
�]���̃j���[�g���̏d�͗��_�ł͎���Əd�͓͂Ɨ����������A�C���V���^�C���͏d�͗��_�����̂��̂Ɍ��т���
���R�Ȏ���ƂȂ�d�͏���d��
�i��ʓI�Ɂj���Θ_�ł͏d�͎͂���̘c�݂����ʎq�_�ł͑��茋�ʂ͊m�肵�Ȃ�
�����������Ƃ��Ǝv�����
�ȗ�0��������m��1��������̃P�[�X���F�߂Ă͂��� �����ܘ_�ʎq�_�]�X�͗Ⴆ�b����
>>453
Equivalent�Ƃ͓����ł���Ƃ������ɋ�����ł�����A��O������悤�ȏꍇ�͂��̂悤�ȕ\���ɂ͂Ȃ�܂����
���O��more accurately�Ƃ܂Ō����Ă��� >>455
���⌾�t�Ȃ��當���ˑ����͂��邵�g�p�҂ɂ����ł���
�Ⴆ�Ύ��ʂƃG�l���M�[�͓����ł���ƌ����Ă�����0�̌��q���G�l���M�[�͎���
���l�ɋȗ�0�̎�����܂߂ďd�͏�ƌ��т��Ă邾�����낤�� �o�q�̃p���h�b�N�X�̐����ɒ[���āA�ȗ��O�̉����x�n����ꑊ�Θ_�ň����邩�ǂ�����
�_�_�Ȃ̂��Ǝv���Ă����̂����A���͋ȗ��O�̉����x�n���d�͏�ƌĂԂ��ǂ������_�_�Ȃ̂��H
���R�Ȏ���̋Ȑ����W�n�͓��ꑊ�Θ_�ň�����B
�Ȑ����W�n�Ő����銵���͂͏d�͂ł���B
�̂ɓ��ꑊ�Θ_�͏d�͂�������B
���ӎ��Ȕw�i�ɂ́A���̎O�i�_�@���ǂ��������邩���Ęb������悤�Ɏv���B
��Ԃɋψ�ɑ��݂��鉽���������ɐG��ċN����ω�������
�����ɋ߂Â��ɂ�ĉ��������������蔲���Ă��܂�����ω����x���Ȃ�
�����ɂȂ�Ɖ�����������S�Ă��蔲���Ă��܂������̕ω����~�܂�
�����������Ƃł����H
���������̂͑n�앶�|�ŗ������������Ǝv����
���Θ_�͈ꎟ�ϊ��ƂЂ��`�̏����ł������������ł���
�A�C���V���^�C�����ē������œ����Ă��炵�����ǂ�����Ă܂蕨���w�̌����͎�ł���Ă����Ă��ƁH
��ł���Ă��Ƃ��āA�������ł��H
�L�~�ɂƂ��Ă͎�Ƃ́u�d�����Ɏ��Ԃ𓐂�ł����傲����v�Ƃ����悤�Ȃ��̂ł���̂͂悭�킩����
�N�͂�������Ȃ��́H�@�d�����ɓ��X�Ƃ���
�N�x
�x�e��
�����
�d����
���낢��\��������
9��-5���������Ζ����Ԃƌ��߂���Ȃ�
>>465
�����ƃK�`�̕����w�����҂��Ǝv���Ă�
�����w�������Ă���Ȏ�݂����Ȋ�����DIY���o�ł������Ȃ́H >>470
��ő��Θ_�v�������Ⴄ���炢�̓V�˂�������ł��傤�� �ŏ��͖{�E����Ȃ��������炱���A�]�v�ȌŒ�ϔO�Ɏז�����Ȃ������̂����ȁB
�t�ɁA����g������͌Œ�ϔO�ŗʎq�_�ɔ��������錋�ʂ�
�d���Ȃ玞�Ԃ��ݔ���玑�����l���l�X�ȃ��\�[�X�𗘗p�ł���Ƃ������_������A
��Ȃ牽�ɂ�����ꂸ�������v�����Ƃ���ɂ��闘�_������B
�ǂ��炪���܂��������̓P�[�X�o�C�P�[�X�����A
�A�C���V���^�C���̔��z�ɂ��ẮA�������v���悤�ɂ�ꂽ���Ƃ����ʂɂȂ������̂����ˁB
�Ă��Ƃ͌��d���ʂ̌�������Ȃ�H
�@�ނƂ��ǂ�����ėp�ӂ����́H
�݊w���̑f�s�s�ǂő�w�Ɏc��Ȃ��������������ĂB
�A�C���V���^�C���͎���Ă�����莩�劈�����ȁB
���܂��炪5ch�ɏ�������Ă�̂͊��S�Ɏ�������͐��Ȃ����ǂȁB
>>474
�g�����@�ނ̓y���Ǝ��������� ��Ńm�[�x���܂��Ď������Ȃ�
The Nobel Prize in Physics 1912
Nils Gustaf Dalén �gfor his invention of automatic regulators for use in conjunction with gas accumulators for illuminating lighthouses and buoys�h
�i����ⓔ���W�Ȃǂ̏Ɩ��p�K�X������Ɏ��t���鎩�����ߋ@�̔����j
����Ȃ̂������w�܂��������������킯��
�ŋߐV�ł��ł��L�����n���̎���̊w���ƂĂ��悩����
>>477
>�y���Ǝ�����
��V�˂Ƃ����ǂ������������̏������Ε������_�͑n���ł��Ȃ��B
�����̐��w�ƉȊw�̒��S���h�C�c�i�h�C�c�ꌗ�j���������Ƃ��K�^�ł���
�A�C���V���^�C���̓X�C�X�������̎���������Ƀ}�b�N�X�E�F���E�w���c�̘_����
���W���Č������A���[�����c�̍u�`�����u���Ă���B
����̊w���Ȃ�p��̘_�����e���Ȃ������ł��Ȃ��ƁA���������������� ���́A�����\�������ނ��Ę_���Ɏd�グ�A�����\���͈���ׂ����i�������閧
>>483
474��477�̓A�C���V���^�C���l���g�����@�ނ̘b�A�ȁB
���������g���Ă���̂͑��Θ_�_���̃C���g���ǂ߂ΗđR �M���M�������x�ߖT�̖�����ɂȂ���Ԃ̃v�����N���̊g����̍l�@�܂łȂ�Ȃ�Ƃ��l�@�\�B
��̖����a��1/2��-1/12��
���R�����v�Z�����Ԃ��Q������
�O����Ԃ���V�t�g����ł��炩���������Č��̌v�Z�����Ԃɖ߂��Ă�B
0�̖����a�ł���0�ɐ���Ƃ͌���Ȃ��B
��^2��0�A�Á�0���l���ɓ���Ă����ġ
�e�����������̈悾������`���Z���o����̂��������`�Ȃ��̂�s�p�ӂɈ����Ǝl�����Z���j�]����B
�f�l�������w�D���̃I�b�T�����
�f�l�������w�D���̃I�b�T���͂���Ȏx���ŗ�ȕ��͂������Ȃ�
���Ȃ��͓��������ǃI�b�T���ł�
���[�����c�ϊ��Ŋp�^���ʂ��ۑ������͎̂����Ƃ����邪
�l�����������͎����łȂ��B
�l���������Ȃ�A
���i�^���̓d�q�̃X�s����1/2�E���o�[�ŕς��Ȃ��v�����N�萔�����s�ςɂȂ�B
>>490
���[�����c�ϊ��Ŋp�^���ʂ͕ۑ�����Ȃ� ��ʑ��ΐ����_�ƃI�C���[���������o�[�[�����̃Ƃ��ȒP�Ɍ��т��B
�O��Ƃ��ăA���L���f�X�̃����߂�Ã@�̋Ɍ��l���������_���Ώ̐��ϊ��ɂ��W����B
�s�m�萫�����ƐU���g�����o�[�[�����Ō��ʂ��B���̐��̌��͐U�����Ă鐢�E�ɕ�܂ꂩ���Ȃ��̂�����A
�藝�������g���Ό������z�������[�v����̂���u�œ������o��B�����ł��H�蒅���Ȃ����Z���L����̗̈�̓_�[�N�}�^�[�̐^��̕ʐ��E���L�����Ă���B
�C���t���[�V�����F���őΏ��Ōv�Z���������z������Ԃɓ�����ꂽ�Ȃ�A�����[�݂��܂����w
�A�C���V���^�C���������ŘM���Ƃ���͌W���̃Ɛ������g���₷���B
�܂�1-1+1-1�c�̖����a��1��-1 ��0��1/2�ȂǂɊϑ��҂̓s���Ő����ɏo����B
�A���[����0�͒ʏ�̃[�������̓_�Ƃ��Ĉ����Ă�̂͑����ԈႢ�B
�����原���̃[���Ɩ����������̃[���Ƃ̓n�b�L���ʂ��̂��낤�B
���`�̎l�����Z�͂ǂ���������l�A���͋Ɍ��l�ōl�����̐ϕ��l�ōl����B
����Ə��w���̏����w�̐}�`���͑㐔�Ɨ��\�̊W�����邩��ؖ����ɔ�ꂽ���͎Q�l�ɂȂ�q���g�����������B
��������̂��s�\�ȓz�������Ȃ���
�����܂Ƃ��Ȑl�͑��ΐ����_�ɂ��č��X�b�����Ƃ��Ȃ�����d���Ȃ�
>>488
���������ǂȂ�
�I�C���[��}�k�W�������Ǝv���܂��ˁB
�I�C���[�̃[�[�^�[���̓j���[�g���̉^���������̋����̋t��掮�ƃs�^�S���X�̒藝���I�Ɏg�����B
���}�k�W�����̌����ɂ̓Ɋւ�������Ɉ��Ď��������B >>496
���w�I�ɐ��������瓝�������ǂƂ͌������
�T���@���Ɗ��Ⴂ���ĂȂ����H >>496
�ς��҂Ɠ��������ǂ͂���Ⴄ
���������ǂ��Ǝv�l���܂Ƃ܂�Ȃ�����Ȃ�̖��ɂ��������
���܂��Ɠ��� ���O�Ɠ����ƌ�����f�l���������
�ɋ���������̂�
���̑̐ϕ\�ʐς̌v�Z���ɂ����ꍇ
�K���}�[�����g���邩��
�x�[�^�[�����֘A���ăn�h�����̌��͌^�Ɋ֘A���邵�A�������_�ɂ����W����Ƃ͎v���킯��B
�O���X�}�����Ƒo�ΐ��Âɂ�����������̂Ŕg���������Ǝ����������q����킯�ŋ����[�X�Ȃ킯�ł��B���l����͑����V���������������ĉ������ȁB
�z�[�L���O�̃u���b�N�z�[���̏������f�l�̂�������ł��̂���C�Â��Ă����Ƃ�����B���ꂩ������l����撣���ĉ������ȁB�A�C���V���^�C���������̌W�������̕\�ʂƑ�������̐ςƂ��đ�����������Ƃ��đ�������ϑz����̂��D���ȑf�l����������ł����B
�f�l��������̕����w��싅�ŗႦ��Ȃ�A���싅�ł����Ȃ���TV�Q�[�����{�[�h�Q�[��������Ă���悤�ȃ��x��
�킩���Ă�Ȃ炭��Ȃ�
�싅�ŗႦ����A�O�����h�ɓ����Ă��Č��@���Ă铪�ア�ߏ��̃K�L��
�������O�����h���ǂ����͋c�_��v����Ǝv����
�����̘b����Ȃ��Ă�������̘b����
��ʑ��ΐ����_�ƒ������_��
�~�����̒Nj��������E������
���L���͒萔G�Ɖ~������
�����B
���������瓯�������������Ă���B
���ǃ[�[�^�[���̐��E�̒萔�B
>>505
�����ɂ��Ă����傤���Ȃ��̂ŕa�@�ɍs���Ă������� ���L���͒萔G�Ɖ~�����ɑ㐔�w�I�ɗ��Ƃ���Ή�������B
�����Ƃ��ă[���ɃL�����Z�����邩
�ς̋t�����Ƃ���
�P�ʌ��ɕϊ����Ėɂ��邩��
���@���g����B
�V�t�g�A��]���g����B
���`�ɍS���Ă�Z�@����������f�ɕ������Ĉ����������č\�z��
�ϕ��Řa���Ƃ邱�Ƃ̐ςݏd�ˁB
�u���b�N�z�[���̒���
�����̕\�ʐς�
�����̑̐ς̖��B
�܂�
�K���}�[���A�x�[�^�[���A
�[�[�^�[���̖��ɂȂ�B
�ł���߂������Ď������Ԃ߂�l���Ĉ��ꂾ��
�ŋ߂ł̓A�C���V���^�C���ƌ�������A
���̂������̐��m�M���i��ōς݁j�̊炪������ł���͉̂���sage
���l����͗��R(�R���v���b�N�X)���킩�鎖����
�f�l���������
�F���̑傫���A�̐ς�e�O�ɂȂ�B
�\�ʐς͉^���ʂƃG�l���M�[�����n���Ő�߂��邯�ljF���̑̐ς��������ƃ[���ɂȂ�B�ۑ������킯���B
�F���萔��e�O��
�Ƃ����Ă��ǂ��낤�Ǝv���B
�ǂ���
���̐��Ƃ��̐��Ɩ�����
�F���̐ς̕\�ʂ̌��_�̓��e�A
�����̔@���B
�ȏ�
�f�l��������ł͂Ȃ��ăL�`�K�C��������Ǝ��̂��ׂ�
�j���[�g���̖��L���͂̉^����������
�����Ȃ�܂�
F��Gm0m1�� ^2/6��Gm0m1��(2)
���ΐ����_�킩��Ȃ��������ǃx�N�g���̓��ς����W�n�Ɉˑ����Ȃ����Ă̂������o������ȒP��������
F��GMm��(2)/R^2
��G((e^�� i)(e^�� i)/1)(M��/2)(m��/3)/R
IF R���� then
F��G((e^�� i )(e^�� i)/1)(M��/2)(m��/3)/��
������0�͓���ĂȂ���
0���܂߂�Ƃ�����
�� ^2=0 �Á�o ���g��
F��G(��^2+1)((e^�� i )(e^�� i)/1)(M��/2)(m��/3)/��
�Ƃ��Ă��悢�B
��ʑ��ΐ����_�̃G�l���M�[�e���\���̌W����1/c^2��P�ʐ��Ƃ���
��(2)�Ɛς��Ƃ�B
��������ΑO�ɓ\�����X����
F��
�����B
��ʑ��ΐ����_�̃G�l���M�[�e���\���̌W���Ƀ�(2)�Ɛς��Ƃ��
8��G��(2)/c^2
=8��^3G ^2(e^��i)(e^��i)(M/2)(m/3)/c
M��m�̓G�l���M�[�e���\��T�Ɉڂ�̂�
��ʑ��ΐ����_�̌W����
8��^3 G ^2 (e^��i)(e^��i)(1/2)(1/3)/c
�ƂȂ�I
�N�\�܂���
�ɂȂ�ߏ��̑|���ł����Ƃ�
�ŏ��̈�ʑ��ΐ����_�̌W����c^4
������w
���K�l�����Ă��{���������Ă邩��
c^2�Ɍ����Ă��܂���w
���߂�
��ʑ��ΐ����_�̌W����
8��^3 G ^2 (e^��i)(e^��i)(1/2)(1/3)/c^2
�ƂȂ�I
���߂��w
���߂߂�
��ʑ��ΐ����_�̌W����
8��^3 G ^2 (e^��i)(e^��i)(1/2)(1/3)/c^3
�ƂȂ�I
�������傱���傢�ł��܂�w
�����Ƃɂ̓{�P�V�l�̉^�]�Ƌ��ƃX�}�z�������I�Ɏ��グ��@�Ă�����Ăق����ƐɊ肤
��ʑ��ΐ����_�̌W����
c^4��P�ʐ��Ƃ���
8��G��(4)/c^4
���l������B
���Ƃ͍D�݂ɉ����Ďg���ĉ�����
8��/c ^4
��E8��8��R���Ƃ��Ă�̂ˁB
1/c^4��
��(2)��(2)/c4=(��^2/6)(��^2/6)/c^4
��
E8�~E8
�Ƃ��W���Ă�ƌ������Ƃ��ˁB
��������ƈ�ʑ��ΐ����_�̌W��
8��G/c ^4��
8��G��(2)��(2)��(2)
�ɂ��Ă��悢�ƂȂ�B
�ʓ|�Ȍ�����������B
�����܂ł��܂Ƃ߂��
F��M m G/R ^2
��
�Ċ����g����
F��M m G��(2)/R ^2
�䂦��
8��G/c^4=8��G��(2)��(2)��(2)
�ƂȂ�B
>>534
�{�P�V�l�̓S�~���S�~�ƔF�����Ȃ������
�ǓƂȃ{�P�V�l�͍\�����������Ă��������a�܂�悤�����܂ł�����ׂ葱���A�ی�����o�ϑ������o�J�ɂȂ�Ȃ� �X���^�C����ԈႢ���Əؖ����Ă��












