■出題1
長さが1の線分だけを使って図形を描きます。
描かれた図形によって、線分どうしの相対的な位置関係が一意に決まる部分があるとき、
その部分は「作図できた」と考えることにします。
(1) 8本で 90°を作図してください。
(2) 8本で 20°を作図してください。
(1)
点Oを頂点にもつ2つの正3角形OAB, OCD を描く。
AとC、BとDが近いとき、点O以外の3点E,F,Gで交差する。
AD // BC // EG ⊥ OF
〔補題〕
2点A,Bを結ぶ、右に凸な折線L1 と 任意の曲線L2 がある。
L1が内側(左)に、L2が外側(右)にあり、交差しないとする。
このとき
L1の長さ < L2の長さ
(略証)
最初に L=L2とする。
L1の第一辺を延長し、L2と交わったところでL2に乗り換える。
→ △不等式により、L2より短くなる。
L1の第二辺を延長し、L2と交わったところでL2に乗り換える。
・・・・
これを繰り返すと、単調に短くなり、最後には L=L1 に至る。(終)
〔系〕
2点A,Bを結ぶ、右に凸な曲線C'がある。
C'に内接する折線L1 と C'の外側の任意の曲線L2 も2点A,Bを結ぶとする。
このとき
L1の長さ < L2の長さ
ぬるぽ
http://2chb.net/r/math/1429353046/224
解析概論スレ5 〔出題1〕
△ABCに対し、同じ平面上の点Pからその3辺BC,CA,ABまたは延長上に引いた垂線の足(垂線と辺との交点)を D,E,F とします。
3直線AD,BE,CFが同一点で交わるとき、点Pを垂足チェヴァ点と呼ぶことにします。
問1 △ABCの3頂点、外心O、垂心Hが垂足チェヴァ点であることを示せ。
問2 Pが垂足チェヴァ点ならば、外心Oに関してPと対称な点P~も垂足チェヴァ点であることを示せ。
f(P) = (BD/DC)(CE/EA)(AF/FB),
とおく。ここで3点 D,E,F は問題文のように定める。
チェヴァの定理より
Pが垂足チェヴァ点 ⇔ f(P)=1
問1
外心Oから辺BCまたは延長上に引いた垂線の足Mは、辺BC中点。
∴ (BM/MC) = 1, 他の2辺についても同様。
∴ f(O) = 1,
チェヴァの定理の逆より、外心Oは垂足チェヴァ点である。
Pが△ABCの垂心Hのとき、HはAD,BE,CFの交点。
∴ 垂心Hは垂足チェヴァ点である。
問2
3点 P,O,P~ から辺BCまたは延長上に引いた垂線の足を D,M,D~ とする。
P, P~は点Oに関して対称。
∴ D, D~ は中点Mに関して対称。
∴ BD = D~C, DC = BD~
∴ (BD/DC)(BD~/D~C) = 1, 他の2辺についても同様。
∴ f(P)f(P~) = 1,
なお、外心Oに関して垂心Hと対称な点はド・ロンシャン点と呼ぶらしい。。。
「数学セミナー」2020年2月号, 日本評論社 (2020)
エレ解 出題1
ド・ロンシャン点Lはオイラー線上にある。
HG:GO:OL = 2:1:3
外接三角形の垂心である。
縦が1、横が√2の長方形の折り紙がある。
この折り紙を縦に3等分する折り方を示せ。
平面上に四つの点があり、その各点はそれぞれ、
ある正方形の四辺上の点であるという。
その正方形を作図せよ。
次のことを証明せよ。
△ABCの各辺を等しい比に内分する点をP、Q、Rとすると、
△ABCの重心と△PQRの重心は一致する。
但し初等幾何で証明すること。
任意の角∠XAYが与えられていて、
その内側に任意の点Pが与えられている。
Pを通る直線を引き、それがAX、AYと交わる点をB、Cとする。
△ABCの面積を最小にするB、Cの位置を求めよ。
任意の三角形の面積を、底辺に垂直な直線で、二等分せよ。
これは、たぶん、フツーの人は、解けない。
これが解けたら、相当な上級者。
自作問題
任意の△ABCの面積を、AB、BCを切る直線で二等分したい。
その直線とAB、BCとの交点をD、Eとするとき、
DEの長さが最小となるのは、BD=BEのときであることを証明せよ。
但し初等幾何で証明すること。
>>50 これは△ABCのことを忘れて、
角Bを同面積に切る直線たちの中でBとの距離が最も遠いものは二等辺三角に切る直線であることを示せばよい
なぜなら直線に切り取られる面積は
(直線とBの距離)×(切り取られた線分DEの長さ)÷2
であり、後者を小さくすることは前者を大きくすることだからである
以下、二等辺三角に切る直線をDE、角BからDEへの垂線(これは角Bの二等分線)の足をHとしておく
これとは別の傾きで同面積を切る直線ℓを考えよう
ℓと平行でHを通る直線ℓ'が切り取る面積はBDEよりも大きい
なぜならℓ'の角Bとの交点をD',E'(仮にD'H<E'Hとしておく、逆でも同様)とすると△DD'HはBDEの内側、△EE'HはBDEの外側にあり、それらの面積比はD'H:E'Hだからである
よってBDEと同じ面積を切り取るℓはℓ'よりも角B側に近くなければいけない
よって直線ℓとBとの距離は直線DEとBとの距離(=BH)より小さい
>>51 >角Bを同面積に切る直線たちの中でBとの距離が最も遠いものは二等辺三角に切る直線であることを示せばよい
という発想は面白い。
しかしℓは必ずHより内側にあるはずだから、
ℓ'が作る△BD'E'が、ℓが作る△BDEより大きいことは明白だから、
△DD'Hと△EE'Hの面積比較は意味がない。
そもそもなぜ△DD'Hと△EE'Hのような変な部分を比較するのかが分らない(笑
何はともあれ回答が寄せられたことはうれしい。
そこで今日の問題。
円があり、その周上に定点Aがあり、円内に定点Bがある。
Bを通る弦をPQとするとき、AP×AQが最大となるようなPQを引け。
>>52 あれ、ℓがHより内側にあるってそんなに明らかですかね?
どんな証明を自作されていたかも良ければ教えてください
>>53 僕は僕の本の次の改訂版で「幾何小問」と題して、
いくつかの初等幾何の問題を扱う予定で、
この問題の証明もそこに書くつもりだから、ここには書かない(笑
しかしHを通る直線で切ると、その三角形が
二等辺三角形BDEより大きくなることは明白である。
だからℓは必ずHより内側になければならない。
ついでにいうと、
>>47の問題も、
初等幾何による証明は知られていない(?)ようなので、
次の改訂版で初等幾何による証明を書く予定だ。
もしかしたら2chの人間が初等幾何による証明を知っているかもしれない、
と思い、出題してみたのだが、今のところ回答がない。
数学塾を経営しているという某数学ブログの作者にも出題してみたが、
今のところ回答がないのだ。
>>54 本を書かれてる方だったんですね
Hを通る直線で切ると二等辺三角の面積より大きくなることはどうやってわかりますか?
(そのために自分はDD'HとEE'Hの面積を比べてしまいましたが…)
>>55 僕は君の
>>51のレスを誤解していたようだ。
君がD、Eと書いているのはℓで切ったときの交点かと思っていた(笑
まさに君が
>>51に書いている通りの理由によって、
△DD'Hと△EE'Hのどちらかが片方より大きくなるのだから、
Hを通る直線で切ると二等辺三角の面積より大きくなるのである。
ちなみに僕が出した本は次の本。
「相対性理論はペテンである/無限小数は数ではない」
「卑弥呼は満鮮にいた」
「馬韓も百済も満州にあった」
いずれもアマゾンのみの販売で、百部限定の自費出版本。
「相対性理論はペテンである/無限小数は数ではない」は
一部に不備があるので、来年改訂版を出す予定。
次のことを証明せよ。
AB=ACの二等辺△ABCがある。
BからABに、CからACに、垂線を立て、それらの垂線の交点をPとする。
BC上に任意の点Qがあり、Qを通りAC、ABに平行線を引き、
それらがAB、ACと交わる点をM、Nとする。
このときPQの延長とMNは直交する。
これは、直交条件の知識がないと、たぶん、解けない。
四角形ABCDがあり、AB=AC=(BD+CD)/2であるとする。
対角線の交点をEとするとき、EA>EDであることを示せ。
∠XAYが与えられており、その角外に点Pが与えられている。
Pを通る直線がAX、AYと交わる点をB、Cとするとき、
△ABCの周の長さが、与えられた長さsに等しくなるように、直線PABを引け。
次のことを証明せよ。
円周上に任意の四点A、B、C、Dがある。
それらの円弧AB、BC、CD、DAの中点をP、Q、R、Sとすると、
PRとQSは直交する。
>>60 中点より
弧PQ=(弧AB+弧BC)/2
弧QR=(弧BC+弧CD)/2
弧RS=(弧CD+弧DA)/2
弧SP=(弧DA+弧AB)/2
よって
弧PQ+弧RS=弧QR+弧SP=半円
Sの向かいの円周上の点をS'とすると
弧PQ=弧S'Rとなるから
中心角QS'を二等分する線ℓは弦PRと直交する
中心角と円周角の関係により弦QSは二等分線ℓと平行になり
弦PRは弦QSとも直交する
なるほど、そのような解法もあるのかと感心した。
では次の問題。
丸山良寛の定理を証明せよ。
実は
>>60を利用すると、丸山良寛の定理が、
wikipedia記載の方法とは別の方法で、証明できる。
ヒント。円に内接する四角形をABCDとすると、
たとえば△ABCの内心は、AとQを結ぶ線上にある。
次のことを証明せよ。
△ABCがあり、その外接円の直径PQが、BCと垂直に交わっている。
QPの延長とBAの延長との交点をR、PQとACとの交点をSとすると、
R、P、S、Qは調和点列をなす。
>>50
DE^2 = |↑DE|^2
= |↑BD - ↑BE|^2
= |↑BD|^2 + |↑BE|^2 - 2(↑BD・↑BE)
= BD^2 + BE^2 - 2 BD BE k(B)
= (BD - BE)^2 + 2 BD BE (1-k(B)),
= (BD - BE)^2 + 2 AB BC (△DBE/△ABC)(1-k(B)),
= (BD - BE)^2 + 2 AB BC (1/2)(1-k(B)), (←題意)
右辺第2項は一定だから
DE は BD=BE のとき 最小になる。
…とやるのは初等的ぢゃないねぇ・・・・
ぬるぽ 次のことを証明せよ。
任意の△ABCの内心をIとする。
△ABCの外接円の周上の任意の点PとIを結び、
その延長が外接円と交わる点をDとする。
Dを中心とし、半径DIの円を描き、
それが△ABCの外接円と交わる点をQ、Rとすると、
△PQRの内心もIである。
線分ABがあり、その中点Mを中心とする円がABと交わっている。
Aから円に割線を引き、円との交点をP、Qとする。
△PQBの面積が最大となるように、割線APQを引け。
ちなみに
>>67の問題は、ある本に、
「容易に証明できる」とだけ書かれていて、証明は書かれていなかったので、
問題として出してみたのだが、誰も答えなかったな(笑
ま、誰も解く気がないのだろうから、それはそれでかまわないが(笑
∠XOYが与えられていて、
OX上に定点Aが、OY上に定点Bが与えられている。
二つの円が、AとBで接し、かつPで外接しているとき、
点Pの軌跡を求めよ。
前
>>65 >>69 Pの軌跡はA,O,Bを頂点とする平行四辺形内に偏平な楕円の1/4を描き、A,BにおいてOX,OYと直交する。
>>69 >>71 ガイジよ、脳みそを幼稚園からつくり直してこい。
>>72 お前、もしかして、はい論破男か(笑
そんなに僕が憎いのか(笑
僕はこのスレで一度もお前らに対して嘲笑的な投稿はしていないぞ(笑
お前がガイジではないなら僕が出した問題くらい簡単に解けるだろう(笑
0.99999……は1ではないことくらい簡単に分かるだろう(笑
ところがお前は初等幾何の問題すら解けないし、
0.99999……は1ではないということすら分っていない(笑
どんなに利口ぶってもお前らがアホであることはとっくに分っている(笑
大学レベルの高度な問題をすらすら解けても
0.99999……は1ではないということすら分らないならアホ以外の何物でもない(笑
カントールはもちろんヒルベルトも高木貞治もその程度のアホだったのである(笑
分るか?(笑
>>72 お前、もしかしてイナの答えを正解だと思ったのか?(笑
しかしイナの答えは不正解である(笑
イナは当てずっぽうで書いているだけだ(笑
その証拠に、証明を書いていない(笑
>>73 >>74 嘲笑しながら「嘲笑していない」と嘘をつくなクズ。
「0.99999……は1ではないということすら分らない」などと捏造して我々や数学者らを中傷するな。
偽の命題には「分かる」という現象も「分からない」という現象も存在しない。それらはお前の捏造だ。
偽の命題に対して存在するのは「偽であると分かる」「偽であると分からない」という現象だ。
お前は中傷やヘイトスピーチのために命題だけでなく存在しない現象すら捏造している。
さらに「分かる」の「か」をわざと削除し、「分る」「分らない」という言葉まで捏造している。
例えばアメリカ人に対して「LとRの発音を違うと思っているアホ」とか「同じ発音であることすら分らないアホ」とか言ったらヘイトスピーチだし、逆に嘲笑されるか袋叩きに逢う。
安達がやってるのはそれと同じで数学者に対するヘイトスピーチであり、すなわち安達は数学差別主義者である。
偽の命題Aと、「Aが分る」「Aが分らない」という現象を捏造し、Aが偽であると分かる数学者を「Aであることすら分らない」と捏造し中傷する。
それが安達によるヘイトの手口であり、常套手段である。
安達のヘイトは愛知トリエンナーレなんぞより遥かに悪質で深刻だ。なぜならあっちは県のイベントだが安達の数学ヘイト本は国会図書館という国の施設に置かれているからだ。非常に由々しき事態だ。
>>56 一部に不備?
お前の本は全部不備だろ。
どうせ数学に対する中傷とヘイトスピーチしか書かれてないんだろ。
>>75 お前は第四のバカか(笑
0.99999……に関しては僕のスレに書くように(笑
ここに書くのはスレ違い(笑
ちなみに0.99999……は1ではないことは、
聡明な人はもちろん、聡明ではない一般大衆も分っているのである(笑
0.99999……=1などと思っているのは
大学でインチキ現代数学を学んだ連中だけである(笑
>>76 こいつはただの池沼(笑
大体、僕に対してこういうレスを書いてくるのは
2chの中でもアホの部類に入る連中である(笑
>>77 お前のスレなどない。
5ちゃんねるを私物化するな。
ヘイトスピーチもいい加減やめろ。
お前の存在自体がスレチだ。
お前が先にそのスレチなヘイトスピーチを
>>73で始めておいてスレチを理由に反論を封殺するのは身勝手すぎる。
そもそもお前自体が数学版において場違いなんだからな。
帝大理学部に何浪もして入った○○とかいう相当頭の悪いやつが過去にいたが、そいつにそっくり。問題文にバグをしこんで、ぐふふとか言ってるオタクで
自分を頭良いと思いこんでるただのガイジ。
ガイジは、おそらく「この問題文のどこに問題が得るんでしょうかね」
とおそらくいう。
返答すれば、そこはそういう意味ではない。と問題をすり替える。多解釈可能な曖昧性を残した問題をここに置く。
ガイジは言う
「証拠はどこにあるんですか。問題文が曖昧であるという証拠は?」
と。
と言う訳で、「ガイジ警報」発令します。
このスレの良識ある民は直ちに安全な場所へ避難してください。
ここも遂にアホバカの巣と化したか(笑
>>78 >>72のバカの投稿はヘイトスピーチではないのか(笑
お前らが僕に対して書いていることはヘイトスピーチではないのか(笑
お前らの僕に対する投稿は全部ヘイトスピーチだ(笑
お前らが僕に対してヘイトスピーチをしないなら、
僕もお前らたいしてアホとかバカとは書かないのだ(笑
分るか?(笑
実際僕はこのスレで
>>73以前に
お前らを嘲笑するようなレスは一度も書いていない(笑
そもそもお前らは僕に対して何でそれほど敵意剥き出しなのか(笑
僕はただ0.99999……は1ではない、
という当り前のことを書いているだけなのに(笑
「
>>72のバカの投稿はヘイトスピーチではないのか(笑
お前らが僕に対して書いていることはヘイトスピーチではないのか(笑
お前らの僕に対する投稿は全部ヘイトスピーチだ(笑」
↑自分はいくらでもヘイトスピーチするが、被害者の反論だけをヘイトスピーチと見なし弾圧。泣き寝入りを強要。他人を奴隷視する身勝手な思想。
「お前らが僕に対してヘイトスピーチをしないなら、
僕もお前らたいしてアホとかバカとは書かないのだ(笑
分るか?(笑」
↑と嘘をついているが、安達は0.999...のスレのパート1の
>>1から相手の態度に関係なく中傷とヘイトスピーチしかしてないない。
「実際僕はこのスレで
>>73以前に
お前らを嘲笑するようなレスは一度も書いていない(笑」
↑これも嘘。実際は
>>52から嘲笑している。
「そもそもお前らは僕に対して何でそれほど敵意剥き出しなのか(笑」
↑お前が中傷ばかりしているからだ。知らばっくれるな。
「僕はただ0.99999……は1ではない、という当り前のことを書いているだけなのに(笑」
↑などと嘘をついてやがるが、安達はこの主張をするより一万倍以上の頻度でこの主張とは無関係な中傷ばかりしている。まあ、この0.9999...は1ではないという主張自体が数学に対するヘイトスピーチだがな。
>>84 お前がこのスレに限らず数学版でやっていることこそ荒らしだ
他人に対する嘲笑や攻撃はどのスレにも書くな
>>85 が現れました。
「ガイジ警報」発令します。
このスレの良識ある民は直ちに安全な場所へ避難してください。
直ちに避難し、以下のことに注意して下さい。
ガイジは、おそらく「この問題文のどこに問題が得るんでしょうかね」
と言うことが懸念されます。
返答すれば、そこはそういう意味ではない。と問題をすり替える。多解釈可能な曖昧性を残した問題をここに置く。
ガイジはまた以下のような発言もするでしょう。
「証拠はどこにあるんですか。問題文が曖昧であるという証拠は?」
間違っても返事などしないようにくれぐれもご注意下さい。
ニュースを訂正します。
先程お伝えしましたガイジは、
>>85 ではなく、
>>83 となります。
失礼いたしました。
遂にこのスレもアホバカの巣と化した(笑
>実際は
>>52から嘲笑している。
バカ(笑
>>52の(笑、は嘲笑ではない(笑
微笑の意味の(笑である(笑
そもそも僕は基本的に微笑の意味で(笑と書いているのだ(笑
分るか?(笑
たとえばお前らがwと書いても、
必ずしも嘲笑の意味ではないのと同じだ(笑
ただ単に微笑ましいという意味でwと書くことだってあるだろ(笑
それと同じだ(笑
分るか?(笑
とにかくスレチなことを書くな(笑
僕を叩きたいなら
>>84のスレに書け(笑
お前自体がスレチの塊なのに何言ってやがる。
ここは数学板であって中傷板ではない。
反論を許さず好き勝手に中傷だけさせろなんて我儘が通ると思うな。
あと嘲笑しておいて「微笑」などと知らばっくれるようだが、
数学板において今後一切他人を不快にする嘲笑用語でしかない「(笑」「分る」「分らない」の使用を禁止する。
それに安達がここでやっている中傷への反論を他のスレに書いたらそれこそスレチだろ。
だからそんなに僕が憎いなら
>>84のスレに書け、
と書いただろ(笑
誰が見ても荒らしをしているのはお前らだ(笑
アホはこれだから困る(笑
中傷で荒らしておいて反論者を荒らし認定する。
自分には中傷権があり、相手には反論権はなく、泣き寝入りし黙って中傷される義務があると思っている傲慢な思想。
アニメとかのアンチと変わらない。
だからそんなに僕が憎いなら
>>84のスレに書け、
と書いただろ(笑
誰が見ても荒らしをしているのはお前らだ(笑
アホはこれだから困る(笑
〔問題〕
AB = 8, AC = 72/7, ∠A = 2∠C のとき ⊿ABCの外接円の半径Rを求めよ。
という問題です。
中学数学の範囲で解けるでしょうか。
(三平方の定理、円周角の定理、トレミーの定理は使えます。)
>>98 計算上、28/√21
但し計算ミスしているかもしれない(笑
三平方の定理、円周角の定理、トレミーの定理だけで解ける問題だ。
次のことを証明せよ。
円周上に点A、B、C、Dがあり、ACとBDが直交しているなら、
A、B、C、Dに於ける円の接線の交点をP、Q、R、Sとすると、
P、Q、R、Sは同一円周上にある。
あるいは、同じことだが、
四角形PQRSが円に内接し、かつ、
点A、B、C、Dで円に外接しているなら、
ACとBDは直交する。
>>98 注意:Rを求めるためには、ほうベキの定理を使う必要あり。
但し、もっと簡単な方法があるかも。
余談
>>61の名解答を読んで、僕は非常に感心した。
なるほど、こういうのをエレガントな解法というのだな、と。
しかし先日、僕はもっと簡単な解法を発見した。
但し、それは通俗的で、面白味がない。
しかし、面白味はないが、簡単といえば簡単である。
ちなみに
>>100の問題は、
>>60の問題と、やや似た問題である。
>>99
正解です!
>>257
∠A の2等分線と外接円の交点をDとする。
∠BAD = ∠DAC = ∠C
円周角の定理により
BD = CD = AB = 8,
対称性より
AD = BC
四角形ABDC は円に内接するから
トレミーの定理より
AD・BC = AB・CD + AC・BD,
AD = BC = 32/√7,
半径ODは弦BCを垂直に2等分する。
その交点をMとおく。
BM = MC = 16/√7,
三平方の定理より
OM^2 = RR - BM^2,
これと
OM = R - MD,
より
R = (BM^2+MD^2)/2MD,
さらに
BM^2 + MD^2 = BD^2,
だから
R = (BD^2)/{2√(BD^2-MB^2)}
= 28 /√21, 前
>>70 >>98トレミーってなんだ? そんなの聞いたこともないやつ使っていいなら正弦定理と加法定理はいいってことだよね。円周角の定理? 中心角の半分てやつか?
2R=8/sinC=72/7sin(180°-3C)
=72/7(sin180°cos3C-cos 180°sin3C)
=72/7{0×cos3C-(-1)sin3C}
=72/7sin3C
=72/7(3sinC-4sin^3C)
9=7(3-4sin^2C)
28sin^2C=12
sinC=√(3/7)
∴R=4/sinC=4√7/√3=4√21/3
>>104 普通はsin(180°-3C)=sin(3C)でいいよ。図書いてみな。
前
>>104 >>105図を書いたら角B=180°-3Cだとわかった。
前
>>106 >>105なるほどsin(180°-3C)=sin3Cだから加法定理は省ける。
>>98 >>98トレミーってなんだ? そんなの聞いたす正弦定理と加法定理はいいってことだよね。円周角の定理? 中心角の半分てやつか?
2R=8/sinC=72/7sin(180°-3C)
=72/7(sin180°cos3C-cos 180°sin3C)
=72/7{0×cos3C-(-1)sin3C}
=72/7sin3C
=72/7(3sinC-4sin^3C)
9=7(3-4sin^2C)
28sin^2C=12
sinC=√(3/7)
∴R=4/sinC=4√7/√3=4√21/3
前
>>106 >>105なるほどsin(180°-3C)=sin3Cだから加法定理は省ける。
>>98 図を書くとB=180°-3C
正弦定理より2R=8/sinC=72/7sin(180°-3C)
=72/7sin3C
=72/7(3sinC-4sin^3C)
9=7(3-4sin^2C)
28sin^2C=12
sinC=√(3/7)
∴R=4/sinC=4√7/√3=4√21/3
次のことを証明せよ。
三次元空間内の曲面として
(x^2)/(a^2)+(y^2)/(b^2)-(z^2)/(c^2)=1
によって記述される一葉双曲面は直線の合併集合である。
直線群
x = a{cosφ + (z/c)sinφ},
y = b{sinφ - (z/c)cosφ},
0≦φ<2π, (パラメータ)
を含む。
>>103 もう少し簡単な計算方法もある。
直径をDEとすると、BD^2=DM・DE
これを利用すると、直径DEをすぐに計算できる。
DEは直径だから
∠DBE = 90°= ∠DMB,
∴ ⊿DBE ∽ ⊿DMB,
∴ DE:DB = DB:DM,
また
DB = AB = 8,
BM = BC/2 = 16/√7,
DM = √(DB^2 - BM^2) = (8/7)√21,
前
>>108 >>109そうだね。加法定理は許可すべきだよね。
>>111 直線
x = a{cosφ + (z/c)sinφ},
y = b{sinφ - (z/c)cosφ},
0 ≦ φ < 2π,
と直線
x = a{cos(φ-ζ) - (z/c)sin(φ-ζ)},
y = b{sin(φ-ζ) + (z/c)cos(φ-ζ)},
-π < ζ < π,
の交点 (x,y) と (φ,ζ) が対応する。
(x/a)^2 + (y/b)^2 = 2/(1+cosζ),
z = c tan(ζ/2),
円Oの内部に、二つの定点AとBがある。
AとBを通り、かつ円Oと内接する円を作図せよ。
前
>>115 >>117 ABの垂直二等分線上に円Oについての当該内接円の中心がある。
前
>>115 >>117 ABの垂直二等分線上に円Oについての当該内接円の中心がある。
1845
学コン・宿題ボイコット実行委員会@gakkon_boycott 9月1日
#拡散希望
#みんなで学コン・宿題をボイコットしよう
雑誌「大学への数学」の誌上で毎月開催されている学力コンテスト(学コン)と宿題は、添削が雑で採点ミスが多く、訂正をお願いしても応じてもらえない悪質なコンテストです。(私も7月号の宿題でその被害に遭いました。)このようなコンテストに参加するのは時間と努力の無駄であり、参加する価値はありません。そこで私は、これ以上の被害者を出さないようにするため、また、出版社に反省と改善を促すために、学コン・宿題のボイコットを呼び掛けることにしました。少しでも多くの方がこの活動にご賛同頂き、このツイートを拡散して頂ければ幸いです。
https://twitter.com/gakkon_boycott/status/1300459618326388737 https://twitter.com/5chan_nel (5ch newer account)
次のことを証明せよ。
点Aから円に引いた接線の接点をBとし、ABの中点をMとする。
Mから円に割線を引き、円との交点をC、Dとする。
ACの延長と円との交点をE、ADと円との交点をFとすると、
ABとEFは平行である。
〔問題〕
平面上の△ABCの辺BC上に点Dをとり、
AB^2 + AC^2 = 2AD^2 + BD^2 + CD^2,
をみたすようにします。
このときDは辺BCの中点Mに限るでしょうか。
数セミ増刊「数学の問題」第2集, 日本評論社 (1978)
●116改
Aから辺BCに下した垂線の足をHとおくと
AB^2 = AH^2 + BH^2,
AC^2 = AH^2 + CH^2,
辺々たせば与式となる。
点Dは辺BCの中点Mと垂足Hに限るでしょうか。
A(a,h) B(b,0) C(c,0) D(x,0) H(a,0)
とおけば
AH = h,
AB^2 = hh + BH^2 = hh + (b-a)^2,
AC^2 = hh + CH^2 = hh + (c-a)^2,
AD^2 = hh + DH^2 = hh + (x-a)^2,
BD = |x-b|,
CD = |x-c|,
AB^2 - AD^2 - BD^2 = -2(x-a)(x-b),
AC^2 - AD^2 - CD^2 = -2(x-a)(x-c),
辺々たすと
0 = -2(x-a)(2x-b-c),
x = a または x = (b+c)/2,
D = H または D = M.
次のことを証明せよ。
定点P、Qがあり、定三角形ABCが、
辺ABがPを通り、辺ACがQを通るように動くなら、
辺BCは、ある定円に接す。
頂角Aが等しく、かつ、周の長さも等しい△ABCのうち、
底辺BCの長さが最小なものを求めよ。
但し証明その他は初等幾何によって行うこと。
前
>>119 >>126 あやとりの紐を壁か板か柱の一点Aに
釘かピンかネジを刺して引っ掛け、
つまり△ABCの頂点を固定し∠Aを決めると、
△ABCが二等辺三角形のとき、
まるで点Aの釘かピンかネジとあやとりをしてるかのように、
辺BCは必然的に最小になる。
∴示された。
>>127 >∴示された。
示されていない(笑
どこにも証明が書かれていない(笑
前
>>126 あやとりの紐を壁か板か柱の一点Aに
釘かピンかネジを刺して引っ掛け、
つまり△ABCの頂点を固定し∠Aを決めると、
△ABCが二等辺三角形のとき、
まるで点Aの釘かピンかネジとあやとりをしてるかのように、
辺BCは必然的に最小になる。
∴AB=ACのとき△ABCの底辺BCは最小
>>129 だからイナよ、どこにも証明が書かれていないではないか(笑
自作問題
△ABCの中に二円があり、
円BはABとBCに接し、円CはACとBCに接し、
かつ、この二円は外接しているとする。
このような二円を作図せよ。
>>131は「分らない問題はここに書いてね」
に出ていた問題を見て思い付いた改作。
元の問題は「二円の面積の和が最小のときの、二円の面積を求めよ」
という問題であった。
二円の面積の和が最小となるのは、
円Bか円Cのどちらかが、△ABCの内接円であるときである。
その理由は、実際に作図してみれば分るが、
△ABCの内心をI、円Bの中心をP、円Cの中心をQとすると、
PQを直径とする円はBCに接しながら動き、
それにつれて、その中心Oは、BIの中点からCIの中点まで動くからである。
仮に円Bが△ABCの内接円であるとき二円の面積和が最小であるとすると、
そのときの円Cの半径は、△ABCの内接円の半径をr、CIの長さをkとすれば、
r(k-r)/(k+r)である。
一部訂正
その中心Oは、BIの中点からCIの中点まで動くからである。
↓
その中心Oは、BI上のPIの中点からCI上のQIの中点まで動くからである。
前
>>129 ぉとこゎ♪ だれ~もみな♪
むくちな♪ へぃ~し~♪
次のことを証明せよ。
点Aから円に引いた接線の接点をB、Cとし、BCの中点をDとする。
Aから円に引いた割線と円との交点をP、Qとすると、
BCは∠PDQを二等分する。
注記
この問題が、解けても解けなくても、
この問題によって、「分らない問題はここに書いてね463」の、
248の問題が、同スレの268の要領で解けることが、分るだろう。
自作問題
△ABCの各辺を等比に内分する点をP、Q、Rとする。
△PQRの面積が最小になるのは、どんなときか。
但し、代数的な証明は不可。あくまで幾何的に証明すること。
注記
この問題は、問題自体は、自作問題ではない。
しかし、幾何的に解け、という条件を付けた点で、
自作問題と言ってもかまわないだろう。
前
>>134😗
>>136 中点。
∵辺を1:tに内分しt→∞とすると、
△PQR→△ABC
限りなく面積は同じ広さに近づく。
t=1なら△PQR=△ABC/4であり、最小である。
>>137 なかなか面白い解答だが、
P、Q、Rを中点にとったとき、そうでないときより
△PQRの面積が小さくなることを、図形的に証明してみよ(笑
次のことを証明せよ。
点Pから円に引いた二本の接線の接点をA、Bとする。
Pから円に割線を引き、弦ABとの交点をQ、
円との交点をR、Sとすると、P、R、Q、Sは調和点列をなす。
余談
>>135の問題が解ける者は、
「分からない問題はここに書いてね463」の
652の問題が解けるだろう。
円の直径上に二点A、Bが、円の中心Oの両側に、ある。
円周上に点Pをとり、P、Aを通る弦と、P、Bを通る弦が、
同じ長さになるように、せよ。
作図題二題
①
任意の三角形と等積な正三角形を作図せよ。
②
△ABCと∠Aを共有し、かつ、これと等積な直角三角形を作図せよ。
作図題二題 その2
次の方程式の根を作図せよ。
① x^2+3x-1=0
② x^2-3x+1=0
前
>>137 >>143 x^2+3x-1=(x+3/2)^2-13/4
x^2-3x+1=(x-3/2)^2-5/4
xy平面にy=x^2+3x-1とy=x^2-3x+1を描くために、
点(-3,-1),(-3/2,-14/3),(0,-1),(0,1),(1/3,1/9),(1,-1),(3/2,-5/4),(3,1)をとり、
2つの合同な下に凸の双曲線を描くよう滑らかにつなぐ。
∴題意は満たされた。
イナよ、そんなのは作図解ではない(笑
そもそも双曲線をどうやって作図するのか(笑
前
>>144 >>145 放物線は中2か中3ぐらいから描くんちごたか?
物理みたいな第1分野か第2分野かどっちがどっちか忘れたけど、あった思たで。
だぁれもフリーハンドでびょんびょん描いてたけどなぁ。黒板とかノートとかに。
作図題二題 その3
①
頂角αと、底辺aと、他の二辺の和sを知って、三角形を作図せよ。
②
頂角αと、底辺aと、他の二辺の差sを知って、三角形を作図せよ。
AB=5、BC=4、CA=3の直角三角形ABCがある。
(斜辺ABはCの左斜め上にあると考えよ。)
CからABに垂線CDを下ろし、DからBCに垂線DEを下ろし、
EからCDに垂線EFを下ろし、FからDEに垂線FGを下ろし、
GからEFに垂線GHを下ろし、HからFGに垂線HIを下ろし、…
というふうに、Cから左巻きの渦のように垂線を下ろしていき、
D、E、F、G、H、I…の極限点をPとする。Pの位置を求めよ。
こういうのは代数計算の問題だから、幾何としての面白味はない。
しかし、けっこう面白い問題だと思うので、出すことにした。
ちなみに答えは載っていなかったから、知らない。
知らないが、これが答えだろうという予想は持っている。
シュメール文明を作るのに
必要最小の幾何学と代数を
考えてた途中で
球の体積の公式を作ってみて
他所の人は微分積分からやってるようだけど
挟み撃ちで
体積の公式の係数を求める方が
かくて簡単だった。
微積分で公式を作るのは理にかなってるのは分かる。しかし
偶然にも整数比を思い描くことしかできないシュメール文明以前の人間には
もっと単純な物が相応しいのでこれでよしとした。
幾何学の初歩の
三角関数の1°を使うことは中学高校大学でもそう巡り会うことなく
使用してる。
シュメール文明以前の人間にsin1°、cos1°、tan1°の数値解、比を導き出させるのに苦労した。思考上で。
整数比しか知らないのだから。
加法定理倍角公式合同相似長さ面積体積を教えるのは大変。
これ無くして、
6°の数値解を得なければ
時計で時間も円周の長さも求めるのが
難しい。
これが出来るとあとは簡単。
時間として暦年月日時分秒が得られるし
ギアも作れる。
天体の運動、地球月太陽の運動も観測できる。
少なくとも一般相対性理論の一歩手前まではいける。
凡人のままならこれで十分。
暦を作る段階で
一月12に分けたり、1週間を7日にしその曜日名を付ける合理的な説明はここでする必要も無いし、弧度法と違い
十進法で角度を360°にする理由もここで述べる必要無い。
お邪魔しました。
作図題二題 その4
大きさの異なる二円がAで交わっている。
Aを通る直線と二円との交点をB、Cとする。
①
ABとACの和が、与長線分sに等しくなるように、直線BACを引け。
②
ABとACの差が、与長線分sに等しくなるように、直線BACを引け。
0D :π
1D:2π
2D:4π
3D:16π
4D:32π
5D:64π
6D:128π
7D:256π
8D:512π
9D:1024π
10D:2048π
11D:4096π
12D:8192π
ここでπは次元の点の単位。
1個2個3個……と数える時の
カウントの単位。
前
>>147 >>149 xy座標の第1象限に題意に従って点Aから順に点Pまでとると、
A(4,3),B(0,0),C(4,0),D(2.56,1.92),E(2.56,0),F(3.4816,0.6912),G(2.56,0.6912),H(2.891776,0.248832),I(2.891776,0.248832),J(2.67943936,0.53194752),K(2.891776,0.53194752),L(2.8153348096,0.6338691072),M(2.8153348096,0.53194752),N(n,0.56863929139),O(2.8153348096,0.56863929139),P(2.83294685987,0.5451565577)
∴示された。
前
>>154 >>149 直線BJの方程式はy=(53194752/267943936)x
約分してy=(1662336/83731373)x
直線CKの方程式はy=-(53194752/110822400)x+53194752/27705600
約分してy=-(5772/12025)x+23088/12025
(1662336/83731373)x+(5772/12025)x=23088/12025
(1662336×12025+5772×83731373)x=23088×83731373
x=23088×83731373/(1662336×12025+5772×83731373)
A(4,3),B(0,0),C(4,0)として、
O(2.8153348096,0.56863929139)
P(2.83294685987,0.5451565577)
Q(2.83294685987,0.56863929139)
Rのx座標はOのx座標より(9/25)(OとPのx座標の差)だけ大きいから、
2.8153348096+(9/25)×0.01761205027=2.8216751477
Rのy座標はPのy座標より(16/25)(OとPのy座標の差)だけ大きいから、
0.5451565577+(16/25)×0.02348273369=0.56018550726
S(2.83294685987,0.56018550726)
直角三角形ABCと直角三角形IJKと直角三角形QRSは相似だが、
同じ位相というか配置というか向きを向いていて、
収束点は半直線BJと半直線CKの交点じゃないかと思う。
前
>>155 >>149 3:4:5の直角三角形の垂線は底辺を9:16に分割する点に垂線の足を下ろす。
直線BJの方程式はy=(3324672/16727771)x
直線CKの方程式はy=-(51998/108225)(x-4)
通分してこれらを解くと、
x=207992×16727771/(3324672×108225+16827771×51998)
=2.82951913
y=207992×3324672/(3324672×108225+16827771×51998)
=0.562371581
∴収束点Pの座標は(2.82951913,0.562371581)と推定する。
イナよ、Pは極限点であって、Oの次の点ではない(笑
前
>>156 O's next Pと極限点Pをタイミングよく出させて引っかける気だな、問題がわるい。
では問題文を訂正しておこう(笑
AB=5、BC=4、CA=3の直角三角形ABCがある。
(斜辺ABはCの左斜め上にあると考えよ。)
CからABに垂線CDを下ろし、DからBCに垂線DEを下ろし、
EからCDに垂線EFを下ろし、FからDEに垂線FGを下ろし、
GからEFに垂線GHを下ろし、HからFGに垂線HIを下ろし、…
というふうに、Cから左巻きの渦のように垂線を下ろしていき、
D、E、F、G、H、I、…の極限点をpとする。pの位置を求めよ。
>>153 0Dで点が1個をπとするなら
円の面積の公式で半径を無限大にして直線を作り、2つの直線が交わる点を1つとる。そうすると円周の長さの公式に従い係数は2πの2つの点で1次元。
2次元の公式の係数は4πになってもらわないとこまる。
長いこと使用された円の面積の公式の係数は4πにしても良いのではなかろうか。
>>160 だから
普通に考える
球の表面積は4πr ^2
となる。
>>1 定義と定理は回転群ですね。
ザックリ言えば。
>>154 から
直線BJの方程式: y = (27/136)x,
直線CKの方程式: y = - 0.48(x-4),
交点p (2176/769, 432/769) = (2.8296488946684…, 0.56176853055917…)
かな?
蛇足だけど、I(2.891776, 0.6912)
更に蛇足だけど、垂線の長さの比は 交互に
BC/AB = DE/CD = FG/EF = HI/GH = JK/IJ = … = 4/5,
CD/BC = EF/DE = GH/FG = IJ/HI = … = 3/5,
よって
⊿ABC:⊿IJK:⊿QRS:… の相似比は {(4/5)(3/5)}^4 = (0.48)^4
>>136 アフィン的(?)解法
適当な正則一次変換により ⊿ABC を辺長1の正三角形に移す。
二辺が x と 1-x で挟角が60°の⊿が3つできる。
その面積は二辺の積 x(1-x) に比例し、x=1/2 (中点) で最大となる。
このとき△P'Q'R' の面積は最小となる。
>>154 から
直線BFの方程式 y = (27/136)x,
直線CGの方程式 y = - (12/25)(x-4),
としても同じ。
⊿ABC:⊿EFG:⊿IJK:⊿MNO:⊿QRS:… の相似比は
- {(4/5)(3/5)}^2 = - (0.48)^2
珍しくスレが進んでいるな(笑
>>159の問題を僕は無限級数の問題と考えた。
Cから上にどれだけ進み、Cから左にどれだけ進むか、を考えた。
初項と第二項をどこに取るかが、この問題のポイントだ。
計算結果はCから上に432/769、Cから左に900/769だから、
>>164と同じ。
実際に作図してもほぼその位置に来るから、これが正解であることは間違いない。
>>166 アフィン幾何という言葉だけは知っているが、何のことか分らない(笑
その答えは代数的解法ではあるが、正解(笑
ちなみにCから上にどれだけ進むかは、
まずF(G)まで3・(4/5)^2・(3/5)^2だけ上がる。これが初項。
次にKの位置までどれだけ下がるかを考えると、
公比-(4/5)^2・(3/5)^2で下がる。
以下はこれの繰り返し。
Cから左にどれだけ進むかは、
まずE(G)まで3・4/5・3/5進む。これが初項。
次にKの位置まで公比-(4/5)^2・(3/5)^2で右に行く。
以下はこれの繰り返し。
これを計算すると上の答えになる。
またまた蛇足
>>164 直線AIの方程式 y = 3 + (x-4)/0.48
>>167 直線AEの方程式 y = 3 + (x-4)/0.48
∠ACp + ∠CAp = ∠ApC = 90°,
tan(∠ABp) = tan(∠BCp) = tan(∠CAp) = (4/5)(3/5) = 0.48
念のために補足しておくと、
次にKの位置までどれだけ下がるかを考えると
↓
次にJ(K)の位置までどれだけ下がるかを考えると
次にKの位置まで公比-(4/5)^2・(3/5)^2で右に行く
↓
次にI(K)の位置まで公比-(4/5)^2・(3/5)^2で右に行く
>>151 作図で90度(垂直)と60度(正三角形)と72度(正五角形)を作れる
これを各々作図で二分していくと90度(45),60度(30,15),72度(36,18,9)となる
これらの組み合わせで作れる角は
45a+15b+9c=3(15a+5b+3c) (a,b,cは任意の整数)
となって3の倍数である6度を作れるので
三角関数を知らなくてもアナログ時計の目盛りを刻むことができる
作図題二題 その5
①
三本の平行線がある。
これらの平行線上に三つの頂点を有する正方形を作図せよ。
②
点Aがあり、その下方に水平な直線があり、その下方に円がある。
これらの点と直線と円周上に頂点を有する正三角形を作図せよ。
但し点と直線と円は、そのような作図が可能な位置と大きさであるとする。
前
>>158 >>149 xy平面上に、
A(4,3)
B(0,0)
C(4,0)
をとる。
辺の比が3:4:5の直角三角形の垂線は底辺を9:16に分割する点に垂線の足を下ろす。
D(2.56,1.92)
E(2.56,0)
F(3.4816,0.6912)
点は分数じゃなく、少数でとる。
位置を実感するためだ。
G(2.56,0.6912)
H(2.891776,0.248832)
I(2.891776,0.6912)
Jのx座標は2.56+(9/25)(2.891776-2.56)
=2.67943936
J(2.67943936,0.53194752)
K(2.891776,0.53194752)
直角△ABCと同じ向きの直角△IJKが描けた。
L(2.8153348096,―――略―――)
M(2.8153348096,0.53194752)
N(―――略―――,0.56863929139)
O(2.8153348096,0.56863929139)
P(2.83294685987,0.5451565577)
Q(2.83294685987,0.56863929139)
直角△ABCと同じ向きの直角三角形がIJKの次に現れるのは直角△QRSで、点A,I,Qと点B,J,Rと点C,K,Sがそれぞれ一直線に並び、3本の直線が極限点Pに集まると予想する。
直線BJの方程式はy=(53194752/267943936)x
53194752=27×1970176
267943936=136×1970176
y=(27/136)x
直線CKの方程式はy=-0.53194752(x-4)/(4-2.891776)
y=-(53194752/110822400)(x-4)
y=-0.48(x-4)
y=-(12/25)(x-4)
通分してこれらを解くと、
x=16×136/(9×25+4×136)
=2176/769
=2.842652808916……
y=27×16/769
=432/769
=0.5617685305591……
∴極限点Pの座標は(2.842652808916,0.5617685305591)と推定する。
イナよ、そこまで計算しなくても、実際は、
△EFGができた時点で、AEとBFとCGの交点を求めれば、
それが極限点pの位置である。
前
>>175 >>176通分をなめてんな。そんな簡単じゃねえぞ。
イナよ、
>>159の問題は、結局は相似の中心を求める問題だから、
△ABCと△EFGの対応点を結べば、それらの交点がpの位置になるのである(笑
分るか?(笑
四角形の一対の対辺、二つの対角線とその夾角、を知って四角形を作図せよ。
(i)
λは実数で 0 < |λ| <1 とする。
↑A_o ≠ ↑B_o から始めて
↑A_{n+1} = ((λ+1)/2)↑A_n + ((λ-1)/2)↑B_n,
↑B_{n+1} = ((λ-1)/2)↑A_n + ((λ+1)/2)↑B_n,
とおくと ↑A_n, ↑B_n は収束する。
↑A_∞ と ↑B_∞ は相異なるか?
(ii)
μは実数で 0 < |μ| <1 とする。
↑C_o から始めて
↑C_{n+1} = (μ-1)↑A_n + 2(1-μ)↑B_n + μ↑C_n,
とおくと ↑C_n も収束する。
B_∞ は A_∞C_∞ の中点であるか?
もうすぐ冬休みなので、中高生向けの問題を二題。
①
△ABCがあり、AB=24、AC=20、外接円の半径=30である。
この三角形の面積を求めよ。
但し三角関数の使用は不可。
②
次のことを証明せよ。
△ABCのBC上にD、Mがあり、ADは∠Aの二等分線、AMは中線である。
CからADに垂線CPを下ろし、その延長がAMと交わる点をQとすると、
QDとACは平行である。
②の問題は中学生には解けないかもしれない。
前
>>179 >>182 △ABCにおいて正弦定理より
2R=60=20/sinA=24/sinC
sinA=1/3
sinC=2/5
BからACに下ろした垂線の足をHとすると、
BH=20(2/5)=24(1/3)=8
ピタゴラスの定理より、
CH=√(20^2-8^2)=4√21
AH=√(24^2-8^2)=16√2
△ABC=(4√21+16√2)8/2
=16√21+64√2
前
>>183訂正。
>>182 △ABCにおいて正弦定理より
2R=60=20/sinB=24/sinC
sinB=1/3
sinC=2/5
AからBCに下ろした垂線の足をHとすると、
AH=20(2/5)=24(1/3)=8
ピタゴラスの定理より、
CH=√(20^2-8^2)=4√21
BH=√(24^2-8^2)=16√2
△ABC=(4√21+16√2)8/2
=16√21+64√2
イナよ、三角関数の使用は禁止(笑
それにお前の答えは間違っているぞ(笑
前
>>184 >>182 △ABCの外接円の半径をRとすると、
20/sinB=24/sinC=2R=60
sinB=1/3
sinC=2/5
BCに対するAの高さは8
△ABCの外接円の中心をOとして、
30/sin∠OBC=30/sin∠OCB=60
sin∠OBC=sin∠OCB=1/2
∠OBC=∠OCB=30°
∠BOC=180°-30°-30°=120°
BC=2Rsin120°
=60(√3/2)
=30√3
△ABC=(1/2)(30√3)8
=120√3
イナよ、三角関数の使用は禁止(笑
それに、お前の答えは間違い(笑
△ABC=(12-12/11)12√3/2+(10+10/11)10√3/2
=120×6√3/11+100×5√3/11
=(720+500)√3/11
=1220√3/11
イナよ、僕がお前をアク禁にしたわけではない(笑
僕も今日はエラーが出て書き込めなかった(笑
それから、
>>188は間違い(笑
前
>>192 前々
>>190 書きこめねえぞこら!
前
>>195 >>182 4√(862+16√2674)=164.407870484……
前
>>196訂正。
>>182 cosA=(24^2+20^2-BC^2)/(2×24×20)
sinA=BC/2R=BC/60
480cosA=576+400-3600(1-cos^2A)
(60cosA)^2-8(60cosA)-2624=0
60cosA=4-√(16+2624)=4-√2640=4-4√165
cosA=(1-√165)/15
sinA=√(166-2√165)/15=(√165-1)/15
△ABC=(1/2)24×20(√165-1)/15
=16(√165-1)
=189.523721259……
前
>>197 >>182 BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2×24×20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA={30-√(900+225×4×41)}/225
=(30-30√42)/225
=(2-2√42)/15
cos^2A=(4+168-8√42)/225
=(172-2√672)/225
sinA=√(225-168+2√672)/15
=√(57+2√672)/15
=(√32+√21)/15
△ABC=(1/2)AB×ACsinA
=(1/2)24×20(√32+√21)/15
=16(4√2+√21)
=64√2+16√21
=163.830879111……
イナよ、今のところ、全部間違い(笑
冬休み中だから、
>>182の問題を継続して出しておく。
中高生の回答に期待する。
前
>>198 マジか。腰痛悪化。イタタタ……
まぁでも、どうれも確信は持てなんだでな。
前
>>200 ぎっくり腰が再発して、
トイレに行けなくて困ってる。
数学やると脳が糖を使うから、
小便したくなる。でも今はだめだ。
腰が痛いから。
動けない。
前
>>201 >>199 三角関数か四角関数か知らんけどsinやcosを使う使わずに拘らず、
正しい数値がまだ出てないってことだよね?
>>202 その通り(笑
戦前は大学入試にも初等幾何の問題がバンバン出たらしい。
だから戦前の生徒なら①の問題は五分で解く。
なぜなら①の問題の解き方は準公理のように知られていたからだ。
ところが今の教育は初等幾何を軽視している。
だから今の生徒は①の問題が解けない。
有名塾とか有名進学校の生徒はどうかは知らないが。
②の問題でも、戦前の生徒なら五分で解く。
前
>>202 >>182 手段は選ばず、とにかく答えを出す。
外接円の中心をOとして、
△OAB=(1/2)24√(30^2-12^2)
=12×6√21
=72√21
△OAC=(1/2)20√(30^2-10^2)
=10×20√2
=200√2
△ABC=△OAB+△OAC-△OBC
=72√21+200√2-(1/2)30×30sin∠BOC
=72√21+200√2-450sin∠BOC
中心角∠BOC=2(π-弦BCについて反対側の円周角∠BAC)
sin∠BOC=sin2(π-∠BAC)
=2sin(π-∠BAC)cos(π-∠BAC)
=2sin∠BAC(-cos∠BAC)
=-2sin∠BACcos∠BAC
=-2(BC/2R)(24^2+20^2-BC^2)/(2×24×20)
=-BC(976-BC^2)/(30×960)
△ABC=72√21+200√2+450BC(976-BC^2)/(30×960)
=72√21+200√2+15BC(976-BC^2)/960
=72√21+200√2+BC(976-BC^2)/64
sin^2∠BAC+cos^2∠BAC=1
BC^2/60^2+(976-BC^2)^2/960^2=1
BC^4-1936BC^2+30976=0
BC^2=1936±√(968^2-30976)
=1936±√906048
作図よりBC=√(1936-264√13)
=2√(484-66√13)
976-BC^2=976-1936+264√13
=264√13-960(<0)
△ABC=72√21+200√2-(960-264√13)√(484-66√13)/32
=72√21+200√2-(30-33√13/4)√(484-66√13)
=366.360495035……
前
>>204 >>182 外接円の中心をOとし、
AOとBCの交点をPとすると、
BOに対するPの高さxは、
PからBOに下ろした垂線の足がBOをt:(30-t)に分割するとして、
24:x=30:(30-t)
x=(4/5)(30-t)
=24-4t/5
30:x=30:t
t=24-4t/5
9t/5=24
t=5×24/9=40/3=x
同様にCOをs:(30-s)に分割する位置にP
から垂線を下ろすと、
COに対するPの高さyは、
s=20-2s/3
5s/3=20
s=12
20:y=30:(30-s)
30y=20(30-s)
30(20-2s/3)=20(30-s)
y=12
△ABC=△OAB+△OAC-△OBC
=72√21+200√2-(1/2)30(40/3)-(1/2)30×12
=72√21+200√2-200-180
=72√21+200√2-380
=232.788162511……
>>182 外接円の中心をOとする.
AとOを通る直線と,Aを除く,外接円との交点をDとする.
BC=a,AC=b,AB=c,AD=x,BD=y, CD=zとする.
ピタゴラスの定理より
c^2+y^2=x^2 (1)
同様に
b^2+z^2=x^2 (2)
i) ∠BACが鈍角の場合
トレミーの定理より
ax=by+cz (3a)
(1)(2)(3a)より
a=b√(1-(c/x)^2)+c√(1-(b/x)^2)
b=20,c=24,x=60を代入して
a=4√21+16√2
ヘロンの公式より
s=(a+b+c)/2=2√21+8√2+22
S=√(s(s-a)(s-b)(s-c))
p=2√21+8√2とおくと,s=p+22,a=2pであるから
S=√((22^2-p^2)(p^2-4))
p^2=32√2√21+212よりq=√2√21とおくとp^2=32q+212であるから
S=√((272-32q)(208+32q))
=2^4 * √(8q+53)
≒163.83
ii) ∠BACが鋭角の場合
トレミーの定理より
cz=ax+by (3b)
(1)(2)(3b)より
a=-b√(1-(c/x)^2)+c√(1-(b/x)^2)
b=20,c=24,x=60を代入して
a=-4√21+16√2
ヘロンの公式より
s=(a+b+c)/2=-2√21+8√2+22
S=√(s(s-a)(s-b)(s-c))
p=-2√21+8√2とおくと,s=p+22,a=2pであるから
S=√((22^2-p^2)(p^2-4))
p^2=-32√2√21+212よりq=√2√21とおくとp^2=-32q+212であるから
S=√((272+32q)(208-32q))
=2^4 * √(-8q+53)
≒17.188
>>206の補足
i) ∠BACが鈍角の場合
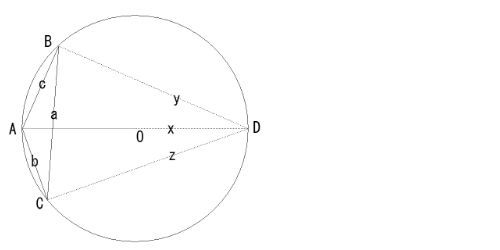
>>206の補足
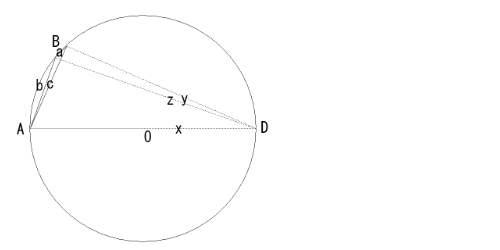
ii) ∠BACが鋭角の場合
ちなみに外接円の半径と三角形の面積の関係
S=abc/4R
は外接円の中心が三角形内部にないので使えない
年の瀬にしょうもない問題を解かせやがって…
と思っていたがなかなか面白かった
来年も数学を楽しめますように
前
>>205 >>207 まだ正解が出てないってわかって安心したよ。
今ぎっくり腰が再発してトランプ状態。
じきに解くから、待っとってくれ。
前
>>213年内決着。
>>182 △ABC=(1/2)AB×ACsin∠BAC
=(1/2)24×20√16875^2-(2051+1800√42)/1125
=139.803668209……
前
>>214補足。
>>182 △OAB=12×√(30^2-12^2)=12×6√21=72√21
△OAC=10×√(30^2-10^2)=10×20√2=200√2
△ABC=四角形OCAB-△OBC
=△OAB+△OAC-△OBC
=72√21+200√2-△OBC
△ABC=(1/2)AB×ACsin∠BAC
=(1/2)24×20sin∠BAC
=240sin∠BAC
△OBC=(30^2/2)sin∠BOC
=450sin∠BOC
=450sin2∠BPC(円周角)
=450sin2∠BAC
=900sin∠BACcos∠BAC
△ABC=72√21+200√2-900sin∠BACcos∠BAC
=240sin∠BAC
(900cos∠BAC+240)sin∠BAC=72√21+200√2
sin∠BAC=(18√21+50)/(225cos∠BAC+60)
(18√21+50)^2/(225cos∠BAC+60)^2+cos^2∠BAC=1
3^4×5^4cos^4∠BAC+2^2×3^3×5^3cos^3∠BAC-3^2×5^2×11×19cos^2∠BAC-2^2×3^3×5^3cos∠BAC+2^2×7×293+2^3×3^2×5^2√42=0
このcos∠BACの4次式を満たすcos∠BACは図より、
cos∠BAC≒-0.8
と予想できる。
4次の係数3^4×5^4と定数項2^2×7×293+2^3×3^2×5^2√42から推定すると、
cos∠BAC=-(2^2×7×293+2^3×3^2×5^2√42)/(3^3×5^4)
=-(2051+1800√42)/16875
=0.81281974857……
sin∠BAC=√{16875^2-(2051+1800√42)^2}/16875
△ABC=240√{16875^2-(2051+1800√42)^2}/16875
=16√{16875^2-(2051+1800√42)^2}/1125
=139.803668209……
前
>>215cos∠BACの符号を訂正。
>>182 △OAB=12×√(30^2-12^2)=12×6√21=72√21
△OAC=10×√(30^2-10^2)=10×20√2=200√2
△ABC=四角形OCAB-△OBC
=△OAB+△OAC-△OBC
=72√21+200√2-△OBC
△ABC=(1/2)AB×ACsin∠BAC
=(1/2)24×20sin∠BAC
=240sin∠BAC
△OBC=(30^2/2)sin∠BOC
=450sin∠BOC
=450sin2∠BPC(円周角)
=450sin2∠BAC
=900sin∠BACcos∠BAC
△ABC=72√21+200√2-900sin∠BACcos∠BAC
=240sin∠BAC
(900cos∠BAC+240)sin∠BAC=72√21+200√2
sin∠BAC=(18√21+50)/(225cos∠BAC+60)
(18√21+50)^2/(225cos∠BAC+60)^2+cos^2∠BAC=1
3^4×5^4cos^4∠BAC+2^2×3^3×5^3cos^3∠BAC-3^2×5^2×11×19cos^2∠BAC-2^2×3^3×5^3cos∠BAC+2^2×7×293+2^3×3^2×5^2√42=0
このcos∠BACの4次式を満たすcos∠BACは図より、
cos∠BAC≒-0.8
と予想できる。
4次の係数3^4×5^4と定数項2^2×7×293+2^3×3^2×5^2√42から推定すると、
cos∠BAC=-(2^2×7×293+2^3×3^2×5^2√42)/(3^3×5^4)
=-(2051+1800√42)/16875
=-0.81281974857……
sin∠BAC=√{16875^2-(2051+1800√42)^2}/16875
△ABC=240√{16875^2-(2051+1800√42)^2}/16875
=16√{16875^2-(2051+1800√42)^2}/1125
=139.803668209……
前
>>216 >>217 やっぱり違うか。
だいたいcos∠BACがこの辺の値だし、
係数から因数分解して出る値だと思うんだよ。
△ABC=240√{1-(7×293+2×3×3√42)/(3^3×5^3)}
=143.545752721……
それかもう少し大きいか。
前
>>218訂正。
>>182 △ABC=240sin∠BAC
=240√(1-((2^2×7×293+2^3×3^2×5^2×√42)/(3^4×5^4))^2)
=220.742462147……
前
>>220 B,Cから外接円に直径BB',CC'および、
外接円の中心について△ABCと点対称な△A'B'C'を描くと、
△AC'A'=20×40√2/2=200√2
△AA'B'=24×12√21/2=144√21
△ABC=△AC'A'+△AA'B'-△A'B'C'
(1/2)24×20sin∠BAC=200√2+144√21-(1/2)40√2×12√21sin∠B'AC'
=240sin∠BAC=200√2+144√21-240√42sin∠BAC
sin∠BAC=(200√2+144√21)/(1+√42)
=(2624√2+656√21)/41
=64√2+16√21
>>198の△ABC=64√2+16√21=163.830879111……と同じになった。
前
>>221 >>182 cos∠BAC=-0.68262866296……
∠BAC=133.049399076……°
と推測する。
前
>>222 >>182 △ABCの外接円の中心をOとすると、
△OABはABを底辺とする二等辺三角形だから、
ピタゴラスの定理より、
△OAB=(1/2)24√(30^2-12^2)
=12√756
=12×6√21
=72√21
同様に△OAC=(1/2)20√(30^2-10^2)
=200√2
四角形OCAB=72√21+200√2
なぜこうなるかは題意により略すしかないが、
弦BCを挟んで∠BACと対峙する∠BOCの円周角は、
向かいあう円周角∠BACの外角と等しいことが関係していて、
△ABCと△OCBの面積比は24×20:30×30
=4×2:5×3
=8:15
△ABC=(8/23)四角形OCAB
=(576√21+1600√2)/23
=213.1437087……
前
>>224訂正。
∠BOCは中心角だから。
BC=2Rsin∠BAC=60sin∠BAC
△ABC:△BPC=24×20:60√(60^2-BC^2)
△ABC=24×20/{24×20+60√(60^2-BC^2)/2}
=480/{480+30√(3600-BC^2)}
=16/{16+√(3600-BC^2)}
ヘロンの公式より△ABC=√s(s-24)(s-20)(s-BC)
s=(24+20+BC)/2
2s=44+BC
s=BC/2+22
s-24=BC/2-2
s-20=BC/2+2
s-BC=-BC/2+22
△ABC=√(484-BC^2/4)(BC^2/4-4)
=16/{16+√(3600-BC^2)}
{16+√(3600-BC^2)}√(484-BC^2/4)(BC^2/4-4)=16
{256+32√(3600-BC^2)+3600-BC^2}(484-BC^2/4)(BC^2/4-4)=16^2=256
{32√(3600-BC^2)+3856-BC^2}(484-BC^2/4)(BC^2/4-4)=256
{32√(3600-BC^2)+3856-BC^2}(122BC^2-BC^4/16-1936)=256
前
>>225 >>182 △ABCの外接円の中心をOとすると、
△OABはABを底辺とする二等辺三角形だから、
ピタゴラスの定理より、
△OAB=(1/2)24√(30^2-12^2)
=12√756
=12×6√21
=72√21
同様に△OAC=(1/2)20√(30^2-10^2)
=200√2
四角形OCAB=72√21+200√2
なぜこうなるかは題意により略すしかないが、
弦BCを挟んで∠BACと対峙する∠BOCの円周角∠BPCは、
向かいあう円周角∠BACの外角と等しいことが関係していて、
△ABCと△PBCの面積比は、
24×20:12√21×40√2
=1:√42
△ABCと四角形OCABの面積比は、
△ABC:四角形OCAB=1:(1+√42/2)
△ABC=四角形OCAB/(1+√42/2)
=2(72√21+200√2)/(2+√42)
=2(72√21×200√2)(√42-2)/38
=(1512√2+256√21)/19
=174.285804432……
前
>>227 円に内接する四角形の一つの内角は、
それと向かいあう角の外角と等しい。
おお、文字数がおうた。
こうだった。
思いだした。
前
>>228 sin∠BAC=sin(1/2)∠BOC=sin∠BPC
△ABC=(1/2)AB×ACsin∠BAC
=(1/2)24×12sin∠BAC
=144sin∠BAC
△BPC=(1/2)PB×PCsin∠BPC=2△OCB
四角形OCAB=72√21+200√2
=△ABC+△OCB
=△ABC+(1/4)PB×PCsin∠BAC
=144sin∠BAC+(1/4)12√21×40√2×sin∠BAC
=(144+120√42)sin∠BAC
sin∠BAC=(72√21+200√2)/(144+120√42)
=(9√21+25√2)/(18+15√42)
=(9√21+25√2)(5√42-6)/3(6+5√42)(5√42-6)
=(945√2-150√2+250√21-54√21)/3(1050-36)
=(795√2+196√21)/3×1014
=(795√2+196√21)/3042
=
∠BAC=
結局は三角関数を使っている。
前
>>229 sin∠BAC=0.6648535358918……=sin138.328905864°
これでいいか?
修正
外接円の中心をOとする.
AとOを通る直線と,Aを除く,外接円との交点をDとする.
BC=a,AC=b,AB=c,AD=x,BD=y, CD=zとする.
ピタゴラスの定理より
c^2+y^2=x^2 (1)
同様に
b^2+z^2=x^2 (2)
i) ∠BACが鈍角の場合
トレミーの定理より
ax=by+cz (3a)
(1)(2)(3a)より
a=b√(1-(c/x)^2)+c√(1-(b/x)^2)
b=20,c=24,x=60を代入して
a=4√21+16√2
ヘロンの公式より
s=(a+b+c)/2=2√21+8√2+22
S=√(s(s-a)(s-b)(s-c))
p=2√21+8√2とおくと,s=p+22,a=2pであるから
S=√((22^2-p^2)(p^2-4))
p^2=32√2√21+212よりq=√2√21とおくとp^2=32q+212であるから
S=√((272-32q)(208+32q))
=2^4 * √(8q+53)
=2^4 * (4√2+√21)
≒163.8308791
ii) ∠BACが鋭角の場合
トレミーの定理より
cz=ax+by (3b)
(1)(2)(3b)より
a=-b√(1-(c/x)^2)+c√(1-(b/x)^2)
b=20,c=24,x=60を代入して
a=-4√21+16√2
ヘロンの公式より
s=(a+b+c)/2=-2√21+8√2+22
S=√(s(s-a)(s-b)(s-c))
p=-2√21+8√2とおくと,s=p+22,a=2pであるから
S=√((22^2-p^2)(p^2-4))
p^2=-32√2√21+212よりq=√2√21とおくとp^2=-32q+212であるから
S=√((272+32q)(208-32q))
=2^4 * √(-8q+53)
=2^4 * (4√2-√21)
≒17.18845687
前
>>230修正。
>>182 (i)∠BACが鈍角の場合、
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2×24×20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA={30-√(900+225×4×41)}/225
=(30-30√42)/225
=(2-2√42)/15
cos^2A=(4+168-8√42)/225
=(172-2√672)/225
sinA=√(225-168+2√672)/15
=√(57+2√672)/15
=(√32+√21)/15
△ABC=(1/2)AB×ACsinA
=(1/2)24×20(√32+√21)/15
=16(4√2+√21)
=64√2+16√21
=163.830879111……
(ii)∠BACが鋭角の場合、
△ABCの面積は3辺が(10,24,30)の三角形の面積の2倍だから、ヘロンの公式より、
△ABC=2√s(s-10)(s-24)(s-30)
s=(10+24+30)/2=32
△ABC=2√32×22×8×2
=2×32√2
=64√2
=212.263986583……
(i)(ii)より示された。
前
>>233訂正。
>>182 ∠BACが鋭角の場合、
弧ABのあいだに頂点Cがある。
△ABC=(1/2)BCsin∠ACB
=10BC(24/60)
=4BC
余弦定理より、
BC^2+20^2-24^2=2×20BCcos∠ACB
BC^2-176=40BC√(1- sin^2∠ACB)
=40BC√{1-(24/60)^2}
=40BC√0.84
=0.8BC√21
辺々二乗しBC^4-352BC^2+30976=13.44BC^2
BC^4-365.44BC^2+30976=0
BC^2=365.44-√{(365.44)^2-30976}
△ABC=4√[365.44-√{(365.44)^2-30976}]
=26.8846039699……
>>238 歩いてない(笑
ところで、この場を借りて要望
ケーキの問題とサル石
http://2chb.net/r/math/1609937007/l50 2chの聡明でまともな連中よ、このサル石というアホに
ケーキを食べ尽くすことはできない。
1/2+1/4+1/8+…は1にはならない。
ということを教えてやってくれ(笑
さて、冬休みも終わったので、次の問題を出すことにする。
作図題二題 その6
①
正方形に内接する正三角形を作図せよ。
但し正方形の頂点と正三角形の頂点が一致する場合は除く。
②
三角形に内接する正方形を作図せよ。
但し正方形の一辺は三角形の底辺と接しているとする。
これからは毎週金曜日に出題しようかと考えている。
なぜ一週間に一問しか出題しないかといえば、
そんなにたくさん出題できるほどネタがないからである(笑
前
>>240 >>182 ∠BACが鈍角のとき△ABC=64√2+16√21=163.830879111……
∠BACが鋭角のとき△ABC=(1728√21+336√37)/73=61.4735513145……
前
>>242訂正。
>>182 ∠BACが鈍角のとき△ABC=64√2+16√21
=163.830879111……
∠BACが鋭角のとき(計算ミスをしていた)
△ABC=5.23593234214……
ちょっとちっさいか?
前
>>242訂正。
>>182 ∠BACが鈍角のとき△ABC=64√2+16√21
=163.830879111……
∠BACが鋭角のとき△ABC=36√2-12√7
=19.1626725127……
前
>>244 >>182 ∠BACが鈍角のとき△ABC=64√2+16√21=163.830879111……
∠BACが鋭角のとき△ABC=64√2-16√21=17.1884568726……
手こずった。
前
>>245過程。
>>182 ∠BACが鈍角の場合、
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2×24×20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA={30-√(900+225×4×41)}/225
=(30-30√42)/225
=(2-2√42)/15
cos^2A=(4+168-8√42)/225
=(172-2√672)/225
sinA=√(225-168+2√672)/15
=√(57+2√672)/15
=(√32+√21)/15
△ABC=(1/2)AB×ACsinA
=(1/2)24×20(√32+√21)/15
=16(4√2+√21)
=64√2+16√21
=163.830879111……
∠BACが鋭角の場合、
弧ABのあいだに頂点Cがある。
△ABC=(1/2)BCsin∠ACB
=10BC(24/60)
=4BC
△ABCにおいて正弦定理よりsinB=20/60=1/3だから、
cosB=2√2/3
20^2-(BC/3)^2={24-(2√2/3)BC}^2
400-BC^2/9=(24-2BC√2/3)^2
BC^2-96BC√2/3+176=0
BC^2-32BC√2+176=0
BC=16√2-√(512-176)
=16√2-√336
=16√2-4√21
△ABC=4BC
=64√2-16√21
=17.1884568726……
鈍角のときと鋭角のときが±違うだけで部分的に対称なかたちになったから、
あってる気がする。
これを作図だけで解けって。
イナよ、三角関数を使ってもいいなら、
フツーの高校生でも、30分もあれば解くぞ(笑
②の問題だって、あることに気付きさえすれば、
今の高校生でも、5分で解くだろう(笑
ところが、その、あることに、なかなか気付かないのである(笑
>182②は「QDとACは平行」という条件をどう導くか、がポイントだな。
実は、射影幾何学(複比)の問題。
または、高校生ならメネラウスの定理か。
ところで、①だけど、
三角関数(余弦定理や正弦定理など)を使うことと、
ピタゴラスの定理を使うことは本質的に同じだよ。
前
>>248 余弦定理とピタゴラスの定理は二乗するけど、
正弦定理は二乗しないところが違うと思う。
>>251 すまん。正確には、
三角関数の余弦定理や正弦定理などを使って問題①を解くことも、
ピタゴラスの定理を含む初等幾何の方法で解くことも、
本質的には同じ
だな。
大雑把にいって、
ピタゴラスの定理 <-> 余弦定理
三角形の面積 <-> 正弦定理
ってところか。
>>250 いい線いっているが、②の問題は射影幾何学(複比)とは関係がない(笑
>>253 それは、複比を使っても決して解けないという意味かい?ww
証明は必ずしも1つではないよ。
多分他にも解法はあるだろうね。
あなたの解答はおそらくメネラウスの定理を使うものじゃないかな?
>250で言ったのは、
「QDとACは平行」が”ある条件”と同値であることを
メネラウスの定理を使って示すことができるが、
複比のある知識を使っても可能だということ。
どちらも射影幾何学の範疇にある定理。
前
>>251 今日は△ABC=519.330645275……だったか、
おっきなりすぎたんでもっかいやり直す。
前
>>255 俺は俺が解いた答案が好きだ。
ハートがきゅんきゅんする。
なんども解いた。
もうすぐそこまで解けてる。
>>254 複比を使って解けるかどうかは考えたことはないが、
そんな難しい知識がなくても解ける問題である(笑
中高生向け問題と銘打っているのは、
射影幾何学(複比)のような、高校では教えない知識を必要とする問題ではないからだ。
あることに気付きさえすれば、フツーの高校生でも簡単に解ける問題である。
前
>>256たったの一行だぜ。たった一行多いだけで書きこめないんだぜ。どうかしてるぜ。
>>182 ∠BACが鈍角のとき、
外接円の中心をOとして、
△ABCにおいて正弦定理より、
24/sin∠BOA=30/sin(π/2-∠BOA/2)
5sin∠BOA=4sin(π/2-∠BOA/2)
=4cos∠BOA/2
半角の公式より、
sin∠BOA=(4/5)√{(1+cos∠BOA)/2}
△OACにおいて正弦定理より、
20/sin∠COA=30/sin(π/2-∠COA/2)
3sin∠COA=2sin(π/2-∠COA/2)
=2cos∠COA/2
半角の公式より、
sin∠COA=(2/3)√{(1+cos∠COA)/2}
△ABC=四角形OCAB-△OBC
=72√21+200√2-450sin(∠BOA+∠COA)
加法定理より、
sin(∠BOA+∠COA)=sin∠BOAcos∠COA+cos∠BOA
sin∠COA
=(4/5)cos∠COA√{(1+cos∠BOA)/2}+(2/3) cos∠BOA√{(1+cos∠COA)/2}
余弦定理より、
cos∠BOA=(900+900-576)/(2×30×30)
=1224/1800
=153/225
=51/75
=17/25
cos∠COA=(900+900-400)/(2×30×30)
=1400/1800
=7/9
sin(∠BOA+∠COA)=(4√21/25)(7/9)√(21/25)+(2/3)(17/25)√(8/9)
=28√21/(25×9)+68√2/(25×9)
△ABC=72√21+200√2-450(28√21+68√2)/(25×9)
=72√21+200√2-56√21-136√2
=16√21+64√2
=163.830879111
∠BACが鋭角のとき、
△ABC=△OBC+△OAC-△OAB
=(1/2)(30×30)(sin∠BOC+sin∠COA-sin∠BOA)
=450sin∠BOC+200√2-72√21
=450sin(∠BOA-∠COA)+200√2-72√21
加法定理より、
sin(∠BOA-∠COA)=sin∠BOAcos∠COA-cos∠BOAsin∠COA
=sin∠BOA(900+900-400)/(2×30×30)-{(900+900-576)/(2×30×30)}sin∠COA
=sin∠BOA(7/9)-(17/25)sin∠COA
sin∠BOA=√(1-17^2/25^2)
=√(625-289)/25
=√336/25
=4√21/25
sin∠COA=√(1-7^2/9^2)
=√(81-49)/9
=√32/9
=4√2/9
sin(∠BOA-∠COA)=(4√21/25)(7/9)-(17/25)(4√2/9)
=(28√21-68√2)/(25×9)
△ABC=450(28√21-68√2)/(25×9)+200√2-72√21
=2(28√21-68√2)+200√2-72√21
=(200-136)√2-(72-56)√21
=64√2-16√21
=17.1884568726……
>>257 この問題、射影幾何学の知識があれば、
あることに気づくのはそう難しくはないけど。
高校の教科書の知識(メネラウスの定理など)だけから、
これを考えつくのは相当難しいと思うわ。ww
知っててよかった射影幾何学
ってとこかな。
>>259 ID:q1OxLAtx君よ、このスレの問題はひとまず置いといて、
ケーキの問題とサル石
http://2chb.net/r/math/1609937007/l50 このスレのサル石というバカに、
ケーキを食べ尽くすことはできない。
1/2+1/4+1/8+…は1にはならない。
ということを教えてやってくれ(笑
このバカを説得できるという自信があるなら投稿してほしい(笑
次のことを証明せよ。
任意の△ABCがある。
AC上に点Dを取り、BDを底辺とし、頂角Eが∠Aに等しい二等辺△EBDを作る。
同様に、AB上に点Fを取り、CFを底辺とし、頂角Gが∠Aに等しい二等辺△GFCを作る。
そうすると、E、A、Gは一直線上にある。
この問題は、正攻法でも解けるが、
幾何に通じた人なら、一瞬で解ける問題である。
前
>>258 >>261 △EBDと△GFCにおいて、
∠B=∠D=∠F=∠C=(π-∠A)/2
2角が等しいから、
△EBD∽△GFC
射影幾何学よりE,A,Gは一直線上にある。
前
>>262別解。
>>261 GFの延長線とEBの交点をH、
EDの延長線とGCの交点をIとすると、
六角形BCIDFHについて、
これら6頂点が同一円周上にあるならば、
ブレーズ・パスカル(当時16歳)の定理によると、
対辺BHとID,HFとCIの延長線の交点E,G
およびDFの延長線とCBの延長線の交点Jの3点は同一直線上にある。
次にAがEG上にあることを示すには、
BFとCDが対辺となるような、
同一円周上に6頂点を持つ六角形を描く必要があると思うが、
おそらく可能だ。
>>262 >射影幾何学よりE,A,Gは一直線上にある。
そんなことは言えない(笑
>>263 的外れ(笑
前
>>263 >>261 題意にしたがって作図すると、
相似な二等辺三角形△EBD∽△GFCの、
頂点E,GのあいだにAがあり、
定規に鉛筆を当てEA方向に引くと、
一瞬で延長線上にGがあるとわかる。
>>265 イナよ、そりゃ作図すれば誰でも
E、A、Gが一直線上にあることは分るのである(笑
問題は、なぜそうなるか、だ(笑
それを証明せよ、というのが数学の問題である(笑
直角三角形の一辺の、斜辺への正射影の長さが、
他の一辺の長さに等しいような、直角三角形を作図せよ。
前
>>265 >>267 📐このように2辺が等しい三角定規をうすく正確に縁取りし、
📏直線定規を使って引きなおし、
三角を尖らせる。
前
>>268 >>267 3辺の比をa,b,c,a<b,a^2+b^2=c^2,sinθ=a/cとおくと、
cosθ=b/c=a/b
c=b^2/a
sinθ=a/c=a^2/b^2=(a/b)^2=cos^2θ=1-sin^2θ
sin^2θ+sinθ-1=0
sinθ=(-1+√5)/2=1.2360679/2=0.6180339……
定規とコンパスにより正五角形を作図し、
頂角から対角線に垂線を下ろすと、
θ=36°の直角三角形が描ける。
前
>>269 >>261 EAもGAも、
BCと平行なんじゃね?
つまりどっちかに傾く理由が、
自然界的にないんだよ。
前
>>270 >261
BCとAGは平行じゃない。
BCとEGも平行じゃない。
メネラウスの定理かなぁ。
イナよ、残念ながら、今のところ、全部外れている(笑
前
>>273 >>261 △ABCは任意だし、点Dも点Fも任意となると、
相似な二等辺三角形が連続写真のように大きさを変え、
それらの頂点は点Aの左右に連なっていく。
まるで接弦定理のように同じ大きさの角を、
ぴったり横付け。
∴EAGは一直線に並ぶ。
前
>>275修正。
>>261 △ABCおよび点D,点Fは任意だから、
点DをACの端点Aにとると∠EDB=∠EAB=(1/2)(180°-∠A)
点FをABの端点Aにとると∠GFC=∠GAC=(1/2)(180°-∠A)
∠EAB+∠A+∠GAC=(1/2)(180°-∠A)+∠A+(1/2)(180°-∠A)=180°
∴点E,点A,点Gは一直線上にある。
>>276 そんな答えでは20点(笑
そんな特殊な場合に成り立つことを証明しても証明とは言えない(笑
どんな場合にも成り立つことを証明しなければ証明とは言えない(笑
∠Aが鈍角な△ABCがある。
辺BC上に、AD×AD=BD×DCとなる点Dを作図せよ。
前
>>276 >>278 Dにコンパスの針を刺して鉛筆が✏Aを通過するように回してBCの延長線との交点B',C'をBB'=CC'となるようにとれればいいから、そのように刺す。
前
>>279違うなぁ。長さじゃないもんね、割合だもんね。
前>>280
>>261
メネラウスの定理で解けないかな。
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;/∩∩ ∩∩ /\;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;/((^o`-。-))/「;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;/っц'υ⌒υ/|;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;∥ ̄UUυυ∥ |;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;∥ □ □ ∥ /|;;;;;;;;;;;;;;;;;;;;;
;;;;;∥____∥/ |;;;;;;;;;;;;;;;;;;;;;
 ̄ ̄ ̄ ̄ ̄∥ |;;;;;;;;;;;;;;;;;;;;;;;
□ □ □ ∥ /|;;;;;;;;;;;;;;;;;;;;;;
_____∥/ |;;;;;;;;;;;;;;;;;;;;;;
 ̄ ̄ ̄ ̄ ̄∥ ,|;;;;;;;;;;;;;;;;;;;;;;;
□ □ □ ∥,彡ミ、 ;;;;;;;;;;;;;;;;;;;;;
_____∥川` , `; ;;;;;;;;;;;;;;;;;;;;;
_____∥/U⌒U、 ;;;;;;;;;;;;;;;;;;;;
 ̄ ̄ ̄ ̄ ̄ ̄;_~U U~ ;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; イナよ、メネラウスでは解けない(笑
>>276の要領で考えればいいのだ。
それが正攻法。
しかし正攻法でなくても、分る人には一瞬で分る問題である。
前
>>281 >>282 自分がメネラウス言うたんやないか。
よう言わんわ。
図描いてだれでも一瞬で、
E,A,Gが一直線に並ぶなぁ思うがな。
イナよ、僕はメネラウスなどと言ったことはない(笑
それは別人のレスだ(笑
長方形ABCDの辺AB上に点Pが与えられている。
辺CD上に点Qを取り、四角形APQDと四角形PBCQの面積比が
√2:1 となるようにせよ。
但しPは、そのような作図が可能な位置に与えられているとする。
△ABCに内接する△PQRを作図せよ。
但し△PQRの各辺は△ABCの各辺に対して垂直でなければならない。
〔補題〕
放物線上にない点Pをとる。
Pを通る2直線L1、L2を曳く。
L1と放物線の交点を A,B とし
L2と放物線の交点を C,D とする。
このとき AP・BP = CP・DP は (一般に) 成り立た
ない。....orz
 ̄ ̄
しかし、放物線の軸と垂直な座標軸をとり
A,B,C,D, P の座標を a,b,c,d, p とすれば
(p-a)(p-b) = (p-c)(p-d)
[分かスレ465-985,986]
>>172 >>269 定規とコンパスにより正五角形を作図する方法
ARを直径とする円Xを描く。
これに内接する正五角形 ABCDEA を作図しよう。
A (-1, 0)
C (cos(36), sin(36))
D (cos(36), -sin(36))
R (1, 0)
T (1/2, 0)
とする。
第二余弦定理より
CT^2 = 1 + 1/4 - cos(36) = 5/4 - φ/2 = 5/4 - 29/36 = 4/9,
CT = DT = 2/3,
直径ARの4等分点Tを中心とし、ARの1/3を半径とする円Yを描く。
円X と 円Y の交点を C および D とする。
ACの垂直2等分線と円Xの交点を B とする。
ADの垂直2等分線と円Xの交点を E とする。
弦AB = BC = CD = DE = EA, (終)
http://suseum.jp/gq/question/3233 次のことを証明せよ。
任意の△ABCの内部に点Pがある。
Pから各辺に下ろした垂線の足をD、E、Fとし、円DEFを描き、
円DEFが各辺と再び交わる点をQ、R、Sとすると、
Q、R、Sに於いて各辺に立てた垂線は一点で交わる。
(略証)
円DEFの中心を O とし、
点Oから各辺に下ろした垂線の足を L, M, N とする。
∠OLD = ∠OLQ = 90゚, OD=OQ より
DL = LQ,
すなわち、点Lは DQ の中点である。
POの延長線と、点Qで辺BCに立てた垂線 との交点を X とすれば
PD // OL // XQ
中点連結定理により
PO = OX
すなわち、点Xは 点Oに関して 点Pと対称な点である。
∴ 点Q,R,S で各辺に立てた垂線は、この点で交わる。(終)
* なお、点Pが⊿ABCの垂心のときは
Q,R,S は各辺の中点であり、そこで立てた垂線は外心で交わる。
この円は九点円である。
〔類題〕
⊿ABCの内部に点Pをとる。
APの延長と辺BCの交点を D,
BPの延長と辺CAの交点を E,
CPの延長と辺ABの交点を F とする。
円DEFと辺BC, CA, AB の交点 (≠ D,E,F) をそれぞれ Q,R,S としたとき、
AQ, BR, CS は一点で交わる。
ただし、たとえば円DEFが辺BCに接している場合には
Q=D と考えるものとする。(木戸晶一郎氏による)
数学セミナー, Vol.50, No.3, 日本評論社 (2011/Mar)
NOTE 「九点円の拡張」p.66-67
(略証)
AD,BE,CFは一点Pで交わるので、チェヴァの定理より
(AF/FB)(BD/DC)(CE/EA) = 1 … (1)
また、方べきの定理より
AF・AS = AE・AR
だから
AF/EA = RA/AS.
同様に、
BD/FB = SB/BQ, CE/DC = QC/CR
これらを (1) に代入すれば
(RA/AS)(SB/BQ)(QC/CR) = 1,
すなわち
(AS/SB)(BQ/QC)(CR/RA) = 1
よって、チェヴァの定理の逆により、
AQ, BR, CS は一点で交わる。 (終)
>>291 正解(笑
このスレは完全に無視されていると思っていたが、
そうでもないことが分っただけでもうれしい(笑
では次の問題。
任意の四角形ABCDがあり、その内部に点Pがあり、
四角形の面積が、APCによって二等分され、
またBPDによっても二等分されているという。
点Pの位置を求めよ。
どうもです。
◇の面積がAPCによって二等分される。
∴ Pは BDの中点を通りACに平行な直線上にある。
◇の面積がBPDによって二等分される。
∴ Pは ACの中点を通りBDに平行な直線上にある。
∴ P は上記2直線の交点にある
>>278 辺ABの延長線上に AB = BB' となる点B' をとる。
辺ACの延長線上に AC = CC' となる点C' をとる。
(⊿AB'C' は、⊿ABC をAの周りに相似拡大したものである。相似比2)
⊿ABCの各辺の垂直二等分線の交点 (外心) をOとして、円ABC を描く。
円ABC と B'C' の交点の一つを D' とする。
AD' と辺BCの交点を D とすると AD = DD'
方べきの定理より
AD^2 = AD・DD' = BD・CD
>>267 (-1/2, ±1/8) を中心とする半径 9/8 の円周を描く。
x軸との交点のうち 小さい方の解は
(-φ, 0) = (-1.618034, 0)
(-φ, 0) と A(1, 0) を直径の両端とする円周を描く。
y軸との交点は B(0, ±√φ) = (0, 1.27202)
A - O(0,0) - B が求める直角三角形。
cos(A) = sin(B) = 1/φ = 0.618034
sin(A) = cos(B) = 1/√φ = 0.786151
>>286 ADの中点M と BCの中点N を結ぶ。
MNとPQの交点を X とすれば
◇APQD : ◇PBCQ = (AP+DQ)/2 : (PB+QC)/2 = MX : XN
∴ MN を √2:1 に内分する点を X とし、PX の延長線と CD の交点をQとする。
ID:HUD3ElaW
>>297以外は正解(笑
>>297は正解かどうか不明だが、座標とか三角法を用いているので不可とする。
では次の問題。
次のことを証明せよ。
鋭角△ABCの垂心をHとし、中線AMの延長が、
円BHCと交わる点をKとすると、MはAKの中点である。
AB, AM, AC を Aの周りに2倍に延長した線分を AB', AM', AC' とする。
⊿ABCと⊿M'CB は、点Mについて対称である。
⊿M'CBの垂心を H' とすれば
BH' ⊥ CM' // AB'
CH' ⊥ BM' // AC'
M'H' ⊥ BC // B'C'
は⊿AB'C' の各辺を垂直に二等分する。
∴ 点H' は ⊿AB'C' の外心 (外接円 の中心) Oである。
円AB'C' を頂点Aに向かって半分に収縮した円ABCは、外心Oを通る。
つまり、点H' を通る。
円ACH'B を点Mについて反転すれば 円M'BHC となる。
∴ 点M' は、中線AMの延長線が 円BHC と交わる点、つまりKである。
定義により、点Mは AM' の中点である。
>>300 なかなかユニークな解法だが、正解(笑
では次の問題。
次のことを証明せよ。
四角形ABCDが円に内接している。
A、B、C、Dに於ける円の接線の交点をP、Q、R、Sとすると、
四角形ABCDの対角線の交点と、
四角形PQRSの対角線の交点は一致する。
対角線AC,BDの交点をXとし、辺BC,DAの延長線の交点をYとする。
6角形 A'ABB'CD が2次曲線に内接している (A'≒A, B'≒B) とする。
パスカルの定理より、接線AA',BB'の交点Pは、直線XY上にある。
6角形 ABC'CDD' が2次曲線に内接している (C'≒C, D'≒D) とする。
パスカルの定理より、接線CC',DD'の交点Rも、直線XY上にある。
∴ 交点XはPR上にある。
同様にして XはQS上にもあるから、題意は成り立つ。
(参考)
郡 敏昭:「射影平面の幾何学」 (1988)
発行 遊星社, 発売 星雲社
6章 §2 パスカルの定理 系6.6 p.110-112
>>302 パスカルの定理は円に内接する六角形に関する定理で、
>>301の問題とは異なる。
また
>>301の問題はA、B、C、Dに於ける接線を使用した問題であり、
その点もパスカルの定理とは異なる。
ゆえに不可とする。厳密解とはいえない。
定点A、Bを通り、定円Cと外接する正方形を作図せよ。
但し、Aはその正方形の一頂点であるとし、
円Cは、その正方形と外接可能な位置にあるとする。
定点Aから引いた二接線のなす角が定角αで、
定点Bから引いた二接線のなす角が定角βであるような円の中心の軌跡を求めよ。
次のことを証明せよ。
△ABCのAでABに接し、かつ内心Oを通る円が、
BCとその延長と交わる点をD、Eとすると、
OCは∠DOEを二等分する。
春休みなので、中高生向け問題を二問
①大円の中に小円がある。
但し二円は同心円でもなく、接してもいない。
この二円の相似の中心を求めよ。
②平面上に二つの相似な三角形がある。
但し二つの三角形の対応辺は平行ではない。
この二つの三角形の相似の中心を求めよ。
〔例2.4.6〕
辺の長さが a,b,c である三角形において,
面積⊿ ≦ (3/4)abc/√(aa+bb+cc),
佐藤(訳) 「美しい不等式の世界」 朝倉書店 (2013) p.89
(略証)
⊿ = (1/4)√{4(aabb+bbcc+ccaa) - (aa+bb+cc)^2} (Heron)
= (1/4)√{4(xy+yz+zx) - (x+y+z)^2}
≦ (1/4)√{9xyz/(x+y+z)} (Schur-1)
= (3/4)abc/√(aa+bb+cc),
* Schur-1
F_1(x,y,z) = (x+y+z)^3 - 4(x+y+z)(xy+yz+zx) + 9xyz
= x(x-y)(x-z) + y(y-z)(y-x) + z(z-x)(z-y) ≧ 0,
〔公式425〕
三角形の内心I、重心G、垂心H、G-Hの中点M、O-Hの中点N とすると
OI^2 = R(R-2r), (Chapple-Euler)
MH^2 - MI^2 = (2/3)r(R-2r),
NI = (1/2)(R-2r),
rは内接円の半径、Rは外接円の半径
等号成立は正△のとき。
[分かスレ466- 425, 495, 678, 690]
(下) の略証
三角形の外接円を重心Gのまわりに (-1/2)倍した円は、
各辺の中点など(*)を通り、9点円とよばれる。
9点円の中心N, 半径は R/2.
内接円の中心I, 半径はr.
[定理31]
三角形の9点円は内接円に接する。(Feuerbachの定理)
∴ NI = (1/2)(R-2r),
(参考書)
清宮俊雄 著「モノグラフ 15.幾何学」矢野健太郎 監修, 科学新興社 (1968/Sep)
§10. p.41
のちに科学新興新社から改訂版が発行された。(1988/Mar)
*) 垂足 (各頂点から対辺に下した垂線の足) と 各頂点と垂心Hの中点を合わせて
9点を通る。
(参考書)
矢野健太郎 著 「幾何の有名な定理」 数学ワンポイント双書36, 共立出版 (1981/Dec)
10 フォイエルバッハの定理 p.103-111
数セミ増刊 「数学100の定理」 日本評論社 (1983/Oct)
「九点円」 p.12-13
点Aがあり、その下方に直線gがあり、g上に点Bがある。
gの下方にgと平行な直線hがある。
Aを通る直線がg、hと交わる点をP、Qとするとき、
BP=BQとなるように直線APQを引け。
但し、Ah間の距離はAB間の距離より短いとする。
このスレは群論のスレらしいし、ネタもなくなってきたので、
出題するのはここらでやめようと思うが、最後に少し書いておこう。
>>125の問題は〇〇〇〇〇の定理というらしい。
面白い問題だと思っていたが、まさか名前が付いているとは思わなかった。
>>302の回答について再考してみたが、やはり間違いである。
パスカルの定理は、次の二つの場合で成り立つ。
①対辺の交点で成立。この場合、交点はすべて円外にある。
②パッブスの定理と同様の結び方で成立。この場合、交点はすべて円内にある。
>>302の回答は①と②をごちゃ混ぜにしている。
〔問題〕
平面上に2つの円
(x-1)^2 + y^2 < 1,
(x+1)^2 + y^2 < 1,
がある。
これらの円をともに内部に含む三角形のうち、
面積が最小のものはどのような三角形か。
[高校数学の質問スレPart414.215]
x<0, x>0 を別々に考え、あとで合体してよい。
直角⊿の 直辺a, b 斜辺c とすると 面積S=ab/2.
内接円の半径rは
r = 2S/(a+b+c)
≦ 2S/{2(1+√2)√S} (*)
= (√S)/(1+√2),
∴ S ≧ (1+√2)^2 = 3 + 2√2,
* a + b + c = a + b + √(aa + bb)
≧ (1+1/√2)(a + b)
≧ (2+√2)√(ab)
= 2(1+√2)√S,
等号成立は a=b すなわち 直角二等辺⊿ のとき
[高校数学の質問スレPart414.222]
〔類題〕
空間内に2つの球
(x-1)^2 + y^2 + z^2 < 1,
(x+1)^2 + y^2 + z^2 < 1,
がある。
これらの球をともに内部に含む四面体のうち、
体積が最小のものはどのような四面体か。
x軸方向に伸びる傾角aの谷の上に2つの球を並べる。
z = |y| tan(a) - z1, z1 = -1/cos(a),
y方向に伸びる、傾角bの屋根を葺く。
z = z2 - |x| tan(b), z2 = (1+sin(b))/cos(b),
四面体のサイズは
⊿x = 2(z2-z1)/tan(b)
⊿y = 2(z2-z1)/tan(a),
⊿z = (z2-z1),
体積は
V(a,b) = (1/6)⊿x・⊿y・⊿z = (2/3)(z2-z1)^3 /(tan(a)・tan(b)),
Vが最小となるのは
a = 1.001631319 (57.38924722°)
b = 0.679837919 (38.95184353°)
のとき
⊿x = 9.77200177
⊿y = 5.05410762
⊿z = 3.94981057
V = 32.5127002274793
これは球の体積 (4π/3)*2 の 3.880917716 倍
〔出題2〕
rは 0<r<1 を満たす定数、θは 0<θ<π を満たす定数とします。
xy平面に2点 P。=(0,0), P_1=(1,0) をとり、
__________
xy平面内の折れ線P。P_1 P_2 … P_n …で次の条件を満たすものを考えます。
_____
・n=1,2,3,…に対して、P_n P_{n+1} = r^n であり、
_____ _____
2つの辺 P_{n-1} P_n と P_n P_{n+1} のなす角が θ または -θ である。
この折れ線が P_2 以後にx軸と交差しないとき、rとθの間に成り立つ関係式を求めてください。
ただし、「交差する」とは1点のみを共有することとします。
0 < θ << 1 の場合
z = r・e^(iθ) とおくと
y(P_n) r sinθ - rr Σ[k=0,n-1] r^k・sin(kθ)
= Im{z - rrΣ[k=0,n-1] z^k}
= Im{z - rr(1-z^n)/(1-z)}
= Im{z - rr(1-z~)/|1-z|^2}
= Im{z - rrz/|1-z|^2}
= Im{z - rrz/(1-2r cosθ +rr)}
= Im{z} (1-2r cosθ)/|1-z|^2
> 0
∴ r・cosθ ≦ 1/2.
〔問題〕
ABCD を円に内接しない四角形とします。
ABCDの対辺の積 AB・CD, AD・BC と 対角線の積 AC・BD =L
を三辺の長さとする三角形が存在することを示して下さいです。
(Lに対する内角は A+C, B+D のうち 180°より小さい方)
(略解)
A+C<180° の場合
頂点Dを中心として
⊿ABDをCD倍して回転
⊿BCDをCD倍して回転
⊿ACDをBD倍
して同長の辺を重ね、⊿ B1-X-B2 を作る。
B1X = AB・CD,
B2X = AD・BC,
B1B2 = AC・BD = L,
また
∠X = A + C, ∠B1 + ∠B2 = B,
LCとともに、CFTのもう一つの主要一般化の一つである遠アーベル幾何学とIUT理論を研究するために、
あえて海外に目を向ける必要がないことは、未来の数学者を志す若い日本人にはこの上なく大きな祝福と言わざるを得ない!
↑
伊原エッセイで伊原先生にダメ出しされていますね。
数学の遠アーベル幾何学と全く新しい理論IUT理論の違いも明確でなく罵倒とホラの類です。
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?https://i.imgur.com/kdxv5LD_d.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?https://i.imgur.com/kdxv5LD_d.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?https://i.imgur.com/9ALyp85.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?https://i.imgur.com/RM13GLl.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?https://i.imgur.com/7zoipRZ.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/X9VGHMY.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/hhhQLHO.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/kKLGvWE.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/JaJlr02.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/U4Y3yOJ.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/utt7kpC.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/vu2xPBY.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/MTfZikX.jpg)
![幾何 [無断転載禁止]©2ch.net ->画像>17枚](https://rz.anime-tube.win/pic.php?http://i.imgur.com/NHNoHXy.jpg)