◎正当な理由による書き込みの削除について: 生島英之とみられる方へ:
面白い問題おしえて~な 27問目 YouTube動画>1本 ->画像>46枚
動画、画像抽出 ||
この掲示板へ
類似スレ
掲示板一覧 人気スレ 動画人気順
このスレへの固定リンク: http://5chb.net/r/math/1532793672/
ヒント:5chスレのurlに http://xxxx.5chb.net/xxxx のようにbを入れるだけでここでスレ保存、閲覧できます。
〔前スレ.964〕
log(2) = 0.30103000,log(3) = 0.47712125 が与えられている。
ここから log(11) の小数第2位の値を求めよ。
>>3 (20/9)^3 = 8000/81 < 11 < 100/9 = (10/3)^2,
3 {1+log(2)-2log(3)} < log(11) < 2 {1-log(3)},
これに数値を入れて
3 * 0.346787486 < log(11) < 2 * 0.522878745
1.04036246 < log(11) < 1.04575749
なお log(11) ≒ 1.041392685
そういえば前スレに貼った画像の閲覧数から、このスレの人口は30人くらいだと分かった
前スレ
>>1000 >
>>998 >テンソル積でうまく表現できるかもですね。
>いま思いついたんだけどGを可換有限群としてGの元gに対応する不定元Agを用意しておいてg行h列がAghである行列にすればよさそう。
>GがZ/2Zをn個直積した場合が今回の例でG=Z/nZの場合が巡回行列の行列式の理論になる。
>その行列式はGの既約指標x(g)にたいしてΣ[g] x(g)Agの形の一次式をn個の指標全体でかけ合わせたものになると思う。
>それで今回の話も巡回行列の行列式の理論も同様に説明できるみたい。
うひゃあ
一挙に一般化しちゃえるのですね素晴らしい
最後のところの証明って付けられますか?
>>4 訂正
(20/9)^3 = 8000/729 < 11
でした。
前スレ993補足
a_1=7
a_(n+1)=a_n+gcd(n+1, a_n)
{a_n}=7,8,9,10,15,18,19,20,21,22,33,36,37,38,39…
https://oeis.org/A106108 b_n=a_(n+1)-a_n
{b_n}=1,1,1,5,3,1,1,1,1,11,3,1,1,1…
https://oeis.org/A132199 c_1=1
c_(n+1)=c_n+lcm(n+1, c_n)
{c_n}=1,3,6,18,108,216,1728,3456,6912,41472,…
https://oeis.org/A135504 d_n=(c_(n+1)/(c_n)-1
d_n=2,1,2,5,1,7,1,1,5,…
https://oeis.org/A135506 おまけ
パズル
10,11,12,13,14,15,16,17,20,22,24,31,100,121,10000,1111111111111111
の16項からなる数列の定義は?
A = Σ[k=0 → ∞] {t^(3k)}/{(3k)!}
B = Σ[k=0 → ∞] {t^(3k+1)}/{(3k+1)!}
C = Σ[k=0 → ∞] {t^(3k+2)}/{(3k+2)!}
を簡単な形で表せ。
>>6 GがZ/2Z×Z/2Zの場合(前スレ
>>994)と同じ。
――
g行h列がAghである行列をMとしxをGの指標とする。
n=#Gとする。
g行目(g≠e)をx(g)倍してe行目にたすとe行目はh^(-1) = h^として
Σ[g]x(g)Agh = Σ[k]x(k)x(h^)Ak = x(h^)Σx(k)A(k)
でe行目がすべてΣx(k)A(k)の倍数だからdet MはD(x) = Σx(k)A(k)でわりきれる。
D(x)の全体は一次独立であったからMはΠ[x]D(x)の倍数で(Ae)^nの係数を比較して
det M = Π[x]D(x)
をえる。
――
>>10 0<t<1の場合、(-∞,0]で切ったlog zの分岐をとって
Σ[k]t^(3k)/(3k)
=(1/3)(Σ[k](t)^k/k + Σ[k](ωt)^k/k + Σ[k](ω^2t)^k/k)
=log (1-t) + log (1-ωt) + log (1-ω^2t)
Σ[k]t^(3k+1)/(3k)
=(1/3)(Σ[k](t)^k/k + ω^2Σ[k](ωt)^k/k + ωΣ[k](ω^2t)^k/k)
=log t + ω^2log ωt + ωlog ωt^2
Σ[k]t^(3k+2)/(3k)
=log t + ωlog ωt + ωl^2og ωt^2
|t|<1の一般の場合はtの偏角に応じて分岐の切り目を変えればいける希ガス。
多分|t|=1でもt≠1ならAbelの定理でいける希ガス。
https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%BC%E3%83%99%E3%83%AB%E3%81%AE%E9%80%A3%E7%B6%9A%E6%80%A7%E5%AE%9A%E7%90%86 自然数nについてn^5-nが5の倍数であることを示せ。(有名問題)
素数pについて一般化できる。
任意の自然数は4個の平方数の和として表せるという。
170以上の自然数はちょうど5個の正の平方数の和として表せることを示せ。
なお、34から169までの自然数もちょうど5個の正の平方数の和として表せることは個別に確認できる。
>>10 >>13
ω = exp(i(2π/3)) = (-1+i√3)/2,
ω~ = exp(i(-2π/3)) = (-1-i√3)/2,
とおくと
A(t) = (1/3){exp(t) + exp(ω・t) + exp(ω~・t)}
= (1/3)exp(t) + (2/3)exp(-t/2)cos((√3)t/2),
A '(t) = C(t) = (1/3)exp(t) + (2/3)exp(-t/2)cos((√3)t/2 + 2π/3),
A "(t) = B(t) = (1/3)exp(t) + (2/3)exp(-t/2)cos((√3)t/2 + 4π/3),
A '''(t) = A(t).
簡単ぢゃねぇ? >>3 >>4 (10/3)^2 - 11 = 81/729 = 1/9,
11 - (20/9)^3 = 19/729
直線で近似すると
1.04036246・0.81 + 1.04575749・0.19 = 1.0413875 < log(11)
ある整数の五乗となる数を五乗数と呼ぶことにする。
13個の五乗数の和で任意の整数を表せることを示せ。
3.891156823326853818078262556719905049852981445670139299627728956
>>22 Wiki 情報ではVaughan and Wooleyの結果で17個以内で出来るってのは示されてるらしいけど13個で出来るん?
(x-1)^3+(x+1)^3+(-x)^3+(-x)^3=6x.
a=a^3+6((a-a^3)/6).
あ、整数か、負の数使うのありなのね。
なら頑張って見ます。
>>17 できた。
3平方定理は既知とする。
http://integers.hatenablog.com/entry/2017/07/05/172017 以下を除く正の整数は5個の正の平方数の和として表せることを示す。
1,2,3,4,6,7,9,10,12,15,18,33
n≦72のとき。
計算機で確認できる。
以下ではn≧72とする。
n≡0 (mod 8)のとき n-1-1 ≡ 6 (mod 8)よりn-1-1は3個の正の平方数で表せる。
n≡2 (mod 8)のとき n-4-4 ≡ 6 (mod 8)よりn-4-4は3個の正の平方数で表せる。
n≡3 (mod 8)のとき n-4-4 ≡ 3 (mod 8)よりn-4-4は3個の正の平方数で表せる。
n≡4 (mod 8)のとき n-1-9 ≡ 6 (mod 8)よりn-1-9は3個の正の平方数で表せる。
n≡5 (mod 8)のとき n-9-9 ≡ 3 (mod 8)よりn-9-9は3個の正の平方数で表せる。
n≡6 (mod 8)のとき n-4-4 ≡ 6 (mod 8)よりn-4-4は3個の正の平方数で表せる。
n≡7 (mod 8)のとき n-4-16 ≡ 6 (mod 8)よりn-4-16は3個の正の平方数で表せる。
n≡1 (mod 72)のとき n-4-36 ≡ 33 (mod 72)よりn-4-36は3個の正の平方数で表せる。
n≡17 (mod 72)のとき n-4-36 ≡ 57 (mod 72)よりn-4-36は3個の正の平方数で表せる。
n≡25 (mod 72)のとき n-4-36 ≡ 57 (mod 72)よりn-4-36は3個の正の平方数で表せる。
n≡33 (mod 72)のとき n-36-36 ≡ 33 (mod 72)よりn-36-36は3個の正の平方数で表せる。
n≡41 (mod 72)のとき n-4-4 ≡ 33 (mod 72)よりn-4-4は3個の正の平方数で表せる。
n≡49 (mod 72)のとき n-16-36 ≡ 69 (mod 72)よりn-16-36は3個の正の平方数で表せる。
n≡57 (mod 72)のとき n-36-36 ≡ 57 (mod 72)よりn-36-36は3個の正の平方数で表せる。
n≡65 (mod 72)のとき n-4-4 ≡ 57 (mod 72)よりn-4-4は3個の正の平方数で表せる。
以上によりnが9の倍数でない場合は示された。
>>26 一般のとき。
n = 9^em (mは9の倍数でない)となるe,mをとる。
mは9の倍数でない奇数であるから1,3,7,15,33の場合を除いては5個の正の平方数の和として表せる。
よってnも表せる。
m=1ならn≧73よりe≧4ゆえn=81・9^(e-4)かつ81=1+4+4+36+36ゆえよい。
m=3ならn≧73よりe≧2ゆえn=27・9^(e-1)かつ27=1+4+4+9+9ゆえよい。
m=7ならn≧73よりe≧2ゆえn=63・9^(e-1)かつ63=1+1+9+16+36ゆえよい。
m=15ならn≧73よりe≧1ゆえn=135・9^(e-1)かつ135=1+1+16+36+81ゆえよい。
m=33ならn≧73よりe≧1ゆえn=297・9^(e-1)かつ297=1+4+4+144+144ゆえよい。
>>21 これ
>>24がほとんど答えやね。
f:Z/480Z→Z/480Zをf(x) = x^5で定めればこれは全射である。
(∵Z/32Z、Z/3Z,Z/5Z上で言えれば十分である。容易ゆえ略。)
よって整数Nに対しN-a-5= 480nを満たす整数a,nがとれる。
このとき
(-n-1)^5+(1-n)^5+(-n-2)^5+(-n+2)^5+(-n-2)^5+(-n+2)^5+(n+3)^5+(n-3)^5+n^5+n^5+n^5+n^5=480n
であるから
N = a^5+(-n-1)^5+(1-n)^5+(-n-2)^5+(-n+2)^5+(-n-2)^5+(-n+2)^5+(n+3)^5+(n-3)^5+n^5+n^5+n^5+n^5
である。
>>21 再挑戦
f:Z/2880→Z/2880は奇数の類かつ3の倍数でない場合に限れば全射である。
(∵Z/64Z、Z/9Z、Z/5Zについてしめせばよい。以下のように計算機でたしかめられる
length $ filter odd $ sort [mod (n^5) 64|n<-[0..63]] -> 32
sort [mod (n^5) 9|n<-[0..8]] -> [0,0,0,1,2,4,5,7,8]
sort [mod (n^5) 5|n<-[0..4]] -> [0,1,2,3,4]。)
与えられたNに対しaを
N≡0 (mod 2)、N≡0 (mod 3)のとき1。
N≡1 (mod 2)、N≡0 (mod 3)のとき2。
N≡0 (mod 2)、N≡1,2 (mod 3)のとき3。
N≡1 (mod 2)、N≡1,2(mod 3)のとき0。
とすればN-a^5は偶数でも3の倍数でもない。
よってN-a^5≡b^5 (mod 2880)を満たす整数bがとれる。
このときN-a^5-b^5=2880nとおけば
N = a^5+b^5+(n+5)^5+(n-5)^5+(-n-4)^5+(-n+4)^5+(-n-3)^5+(-n+3)^5+n^5+n^5
である。□
10個でいけた?
>>30 正解です。すごい、越された…想定していたのは
(n+8)^5 + (n-8)^5 - (4n+1)^5 - (4n-1)^5 + 2・(4n)^5 - 2・n^5 = 40920n = 2^3・3・5・11・31n
を利用するものでした。(この式だとmod11,31でどうしても残り5つの五乗数が必要になります)
>>17 N-169 が4個の平方数の和のとき
13^2 をたす。
N-169 が3個の平方数の和のとき
5^2 + 12^2 をたす。
N-169 が2個の平方数の和のとき
3^2 + 4^2 + 12^2 をたす。
N-169 が平方数のとき
1^2 + 2^2 + 8^2 + 10^2 をたす。
N-169=0 のとき
1^2 + 2^2 + 2^2 + 4^2 + 12^2.
(//ja.wikipedia.org/wiki/四平方定理)
N.C.Ankeny: "Sums of three squares" (1957) は2次形式の理論を使うし、難しそう。
>>17 >>32 〔ラグランジュの四平方定理〕(1770)
すべての自然数は高々四個の平方数の和で表わされる。
オイラーの四平方恒等式
(aa+bb+cc+dd) (ww+xx+yy+zz)
= (aw+bx+cy+dz)^2 + (ax-bw+cz-dy)^2 + (ay-bz-cw+dx)^2 + (az+by-cx-dw)^2
により、各々高々四個の平方数の和に表わされる二数の積は、高々四個の平方数の和で表わされる。
従って、全ての素数に関して高々四個の平方数の和で表わされることを証明すれば十分である。
素数2に関しては 2 = 1^2 + 1^2 より明らかであある。
次に奇素数pについて証明する。
p-1 が法pに関して平方剰余であれば、
s^2 ≡ -1 (mod p)
s^2 + 1^2 + 0^2 = f・p
となる {s,f} が存在する。
p-1 が非剰余であれば、1≦k<p-1 で kが平方剰余、k+1が非剰余となるものが存在する。
(-1)(k+1) は二個の非剰余の積であるから平方剰余である。従って、
s^2 ≡ k (mod p)
t^2 ≡ -(k+1) (mod p)
s^2 + t^2 + 1^2 = f・p
は解 {s,t,f} をもつ。
その解の中でfが最小になるものを選ぶと f=1 であることを証明する。(無限降下法?)
(以下略
>>16の正解
(証明1)
mod 5で
n≡0のときn^5-n=0≡0
n≡1のときn^5-n=0≡0
n≡2のときn^5-n=30≡0
n≡3のときn^5-n=240≡0
n≡4のときn^5-n=1020≡0
よってn^5-n≡0 ■
(証明2)
n^5の下1桁とnの下1桁は一致するからn^5-nは10の倍数
よってn^5-nは5の倍数 ■
(証明3)
唐突だがn^5-n+5(-n^3+n)を考えると
n^5-5n^3+4n
=n(n^4-5n^2+4)
=n(n^2-1)(n^2-4)
=n(n+1)(n-1)(n+2)(n-2)
連続する5数のうちいずれかは5の倍数だからn^5-n+5(-n^3+n)は5の倍数
よってn^5-nも5の倍数 ■
(一般化)
素数pについて、nがpと互いに素のときn^(p-1)-1はpの倍数(フェルマーの小定理)
よってn(n^(p-1)-1)は常にpの倍数 ■
>>32正解
元ネタはWikipediaのその記事
(模範解答)
問題文より、任意の自然数は高々4個の正の平方数の和として表せる。
また、169は
169=13^2=5^2+12^2=3^2+4^2+12^2=1^2+2^2+8^2+10^2
のように1個から4個の正の平方数の和として表せる。
170以上の自然数nについて、
n-169がk個の正の平方数の和として表せるとき、169を4-k個の正の平方数の和として表せば、
nはちょうど5個の正の平方数の和として表せる。 ■
>>26 Kはちょうど3個の正の平方数の和で表せる⇒8を法としてK≡0,1,2,3,4,5,6
は真だけど
逆は言えないんじゃないかなあ
>>16の類題
自然数nについてn^8-n^2が9の倍数であることを示せ。
>>36 逆の証明が
>>26のリンク先にあるやん。
(x^2+4)/(x^2-4)が純虚数になる複素数xとは?
図形的に見ると計算もほとんど無くおわる
>>40 X^2が±4にならない絶対値が2の複素数だから
|x|=2、x≠±2、2i
ヒント大杉
>>37 n^8 -n^2 = nn(n^3 +1)(n^3 -1),
n=3m のとき nn = 9mm ≡ 0 (mod 9)
n=3m+1 のとき n^3 -1 = (3m+1)^3 -1 ≡ 0 (mod 9)
n=3m-1 のとき n^3 +1 = (3m-1)^3 +1 ≡ 0 (mod 9)
>>40 0 = 2 Re{ (xx+4)/(xx-4) }
= (xx+4)/(xx-4) + (x~x~+4)/(x~x~-4)
= 2(|x|^4 -16)/{(xx-4)(x~x~-4)}
= 2(|x|^4 -16)/{(x+2)(x-2)(x~+2)(x~-2)}
= 2(|x|^2 +4)(|x|+2)(|x|-2)/(|x+2||x-2|)^2
∴ |x|=2,x≠±2
>>37 n^8 - n^2 = nn(n^6 -1),
n=3m のとき nn = 9mm ≡ 0 (mod 9)
nが9と素であるとき n^6 -1 = n^φ(9) -1 ≡ 0 (mod 9)
ここに、φ(9) = 6 は 1~8 のうち9と素であるものの数(オイラーのtotient函数)
>>37は
>>34のように解き方は色々あるが、例えば
mod 9で
n^2≡0,1,4,-2
k≡0のときk^4-k=0≡0
k≡1のときk^4-k=0≡0
k≡4のときk^4-k=252≡0
k≡-2のときk^4-k=18≡0
この形式の問題をどうやって作ったかというと
nが3の倍数のときn^3≡0
その他のときn^3≡1,-1
みたいなのを見つけて来て
n^2(n^3-1)(n^3+1)=n^8-n^2
という式を組み立てた
次数が小さいほど芸術点が高い
>>34 (さらなる一般化)
素数pについて、φ(p^k)=p^k-(p^k)/p=(p^(k-1))(p-1)だから
nがpと互いに素のときn^{(p^(k-1))(p-1)}-1はp^kの倍数(オイラーの定理)
よって[n^k][n^{(p^(k-1))(p-1)}-1]は常にp^kの倍数 ■
>>26 1≦n≦33 のとき
1, -
2, -
3, -
4, -
5, (1,1,1,1,1)
6, -
7, -
8, (1,1,1,1,2)
9, -
10, -
11, (1,1,1,2,2)
12, -
13, (1,1,1,1,3)
14, (1,1,2,2,2)
15, -
16, (1,1,1,2,3)
17, (1,2,2,2,2)
18, -
19, (1,1,2,2,3)
20, (1,1,1,1,4), (2,2,2,2,2)
21, (1,1,1,3,3)
22, (1,2,2,2,3)
23, (1,1,1,2,4)
24, (1,1,2,3,3)
25, (2,2,2,2,3)
26, (1,1,2,2,4)
27, (1,2,2,3,3)
28, (1,1,1,3,4)
29, (1,1,1,1,5), (1,1,3,3,3), (1,2,2,2,4)
30, (2,2,2,3,3)
31, (1,1,2,3,4)
32, (1,1,1,2,5), (1,2,3,3,3), (2,2,2,2,4)
33, -
>>26 34≦n≦72 のとき
34, (1,2,2,3,4)
35, (1,1,1,4,4), (1,1,2,2,5), (2,2,3,3,3)
36, (1,1,3,3,4)
37, (1,1,1,3,5), (1,3,3,3,3), (2,2,2,3,4)
38, (1,1,2,4,4), (1,2,2,2,5)
39, (1,2,3,3,4)
40, (1,1,1,1,6), (1,1,2,3,5), (2,3,3,3,3)
41, (1,2,2,4,4), (2,2,2,2,5)
42, (2,2,3,3,4)
43, (1,1,1,2,6), (1,1,3,4,4), (1,2,2,3,5)
44, (1,1,1,4,5), (1,3,3,3,4), (2,2,2,4,4)
45, (1,1,3,3,5), (3,3,3,3,3)
46, (1,1,2,2,6), (1,2,3,4,4), (2,2,2,3,5)
47, (1,1,2,4,5), (2,3,3,3,4)
48, (1,1,1,3,6), (1,2,3,3,5)
49, (1,2,2,2,6), (2,2,3,4,4)
50, (1,1,4,4,4), (1,2,2,4,5)
51, (1,1,2,3,6), (1,3,3,4,4), (2,2,3,3,5)
52, (1,1,3,4,5), (2,2,2,2,6), (3,3,3,3,4)
53, (1,1,1,1,7), (1,1,1,5,5), (1,2,4,4,4), (1,3,3,3,5), (2,2,2,4,5)
54, (1,2,2,3,6), (2,3,3,4,4)
55, (1,1,1,4,6), (1,2,3,4,5)
56, (1,1,1,2,7), (1,1,2,5,5), (1,1,3,3,6), (2,2,4,4,4), (2,3,3,3,5)
57, (2,2,2,3,6)
58, (1,1,2,4,6), (1,3,4,4,4), (2,2,3,4,5)
59, (1,1,2,2,7), (1,1,4,4,5), (1,2,2,5,5), (1,2,3,3,6), (3,3,3,4,4)
60, (1,3,3,4,5)
61, (1,1,1,3,7), (1,1,3,5,5), (1,2,2,4,6), (2,3,4,4,4), (3,3,3,3,5)
62, (1,2,2,2,7), (1,2,4,4,5), (2,2,2,5,5), (2,2,3,3,6)
63, (1,1,3,4,6), (2,3,3,4,5)
64, (1,1,1,5,6), (1,1,2,3,7), (1,2,3,5,5), (1,3,3,3,6), (2,2,2,4,6)
65, (1,4,4,4,4), (2,2,2,2,7), (2,2,4,4,5)
66, (1,2,3,4,6), (3,3,4,4,4)
67, (1,1,2,5,6), (1,2,2,3,7), (1,3,4,4,5), (2,2,3,5,5), (2,3,3,3,6)
68, (1,1,1,1,8), (1,1,1,4,7), (1,1,4,5,5), (2,4,4,4,4), (3,3,3,4,5)
69, (1,1,3,3,7), (1,3,3,5,5), (2,2,3,4,6)
70, (1,1,4,4,6), (1,2,2,5,6), (2,2,2,3,7), (2,3,4,4,5)
71, (1,1,1,2,8), (1,1,2,4,7), (1,2,4,5,5), (1,3,3,4,6)
72, (1,1,3,5,6), (1,2,3,3,7), (2,3,3,5,5), (3,3,3,3,6)
>>43
1~q-1 のうち qと素であるもの(正則元)の全体は乗法群Gをなす。
単位元は 1、 #G = φ(q)
n∈G が生成する巡回部分群を <n> = H とすると、
#H | #G (←ラグランジュの定理)
n∈G の位数はφ(q)の約数。
∴ n^φ(q) ≡ 1 (mod q) -1≦α≦1とする.
円の面積を2等分する曲線Cについて、
Cの長さをL、Cにより区切られた円周の短い方の長さをSとする
(1)L+αSが最小となるようなCが存在することを示せ.
(2)L+αSが最小となるとき、Cと円周のなす角はarcsin(α)となることを示せ.
(3)円の半径を1として、L+αSの最小値を求めよ.
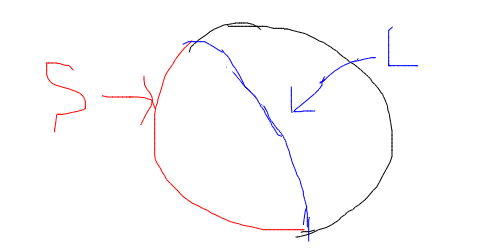
>>50 (2)については円でなくても一般のC^1曲線でも成り立ちますがそれだとあまりに証明が難しいので円にしました
α=0のときCは直径じゃないの?
そのときなす角はπ/2だと思うけど、arcsin(0) = 0になってしまう??
>>52 あーごめんなさいarccos(α)の間違いでした
正の整数 n,k について、
n√2の整数部分を数列{an}とする。
また、全体を正の整数として、{an}の補集合を小さいものから順に並べたものを{bk}とする。
このとき、n=kにおいてbk-an=2nとなることを、(1/√2)+1/(2+√2)=1となることを利用して証明せよ。
>>1解けたよ。前スレの952
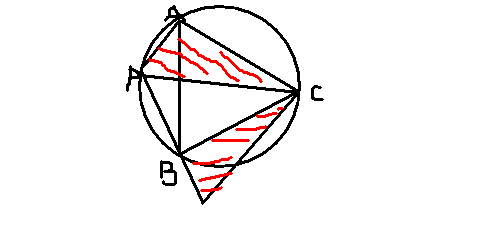
正五角形の対角線と正六角形を二分する線が一致するように正五角形内部に正六角形の半分を描くと、
分岐点と頂点を結ぶ線分の長さは(対角線の半分)か(1-対角線の半分)のどちらかになる。
分岐点と分岐点の距離は(対角線の半分)。
5つの頂点を結ぶ曲線(シオマネキのハサミのような)
=1+(対角線の半分)×3+(1-対角線の半分)×2
=1+{(1+√5)/4}×3+{1-(1+√5)/4}×2
=1+(3/4)(1+√5)+(1/2)(3-√5)
=(13+√5)/4
=3.8090167……
>>57 分岐点と頂点を結ぶ線分の短い方の長さは(1-対角線の長さ)にはなりませんよ
A=分岐点と頂点を結ぶ線分の長い方
B=分岐点と頂点を結ぶ線分の短い方
C=正五角形の一辺
とすると
AとCの挟角が12°ってことが分かって
余弦定理を使えばBの長さは0.30266...になる
そうするとネットワークの長さは4.0323...になって単に辺のみを結ぶよりも長くなってる
1,2,3,5,6,9,11,17,29,41を除く4の倍数ではない自然数は4つの正の平方数の和で表される事を示せ。
>>59 辺のみの解4より大きくなるのは、分岐点の角ぜんぶが120°になってないからで、そのAとBの角が120°になるように長さを調整すると、正弦定理より
A=0.85810…
B=0.24007…
分岐点と分岐点の距離は 1-B
これらからネットワークの長さは3.95629…
4未満にはなる
>>57 >>59 正五角形を P1-P2-P3-P4-P5
正六角形の半分を P1-Q2-Q3-P4 とする。
分岐点の角ぜんぶが 120゚ にはなっていない。
>>61 A は対角線 P1-P4 の半分で
A = (1/4)tan(72゚) = (1/4)√(5+2√5) = 0.769420884293813350642572644009227456
P2-Q2,P3-Q3 は第二余弦定理から
B = √{AA -2AC・cos(12゚) +CC} = 0.2946084067614508837941816613267963
P1-P2-P3-P4 は
C = 1
したがってネットワークの長さは
3A + 2B + C = 3.897479466404341819516081254681275 < 4
単に辺のみを結ぶよりも長くなるのは おかしい。
>>62 訂正スマソ
A は対角線 P1-P4 の半分で
A = 1/{4sin(18゚)} = (1+√5)/4 = 0.809016994374947424102293417182819
P2-Q2,P3-Q3 は
B = √{AA+CC-2AC・cos(12゚)} = 0.2680157330941872201843362931855557
辺 P1-P2-P3-P4 は
C = 1
したがってネットワークの長さは
L = 3A + 2B + C = 3.96308244931321671267555283792 < 4
>>57
[前スレ.952] の解は
正五角形 P1-P2-P3-P4-P5 の一辺 P1-P5 に
1×A の長方形P1-Q2-Q4-P5 を貼る。
点Q3 を
∠P1-Q2-Q3 = 120゚
∠Q2-Q3-Q4 = 120゚
∠Q3-Q4-P5 = 120゚
となるようにとる。
分岐点の角ぜんぶが 120゚ になるように A,B を決める。
P1-Q2、Q4-P5 は 正弦定理より
A = (2/√3)sin(42゚)
= 0.772645471408608606145454411856338206414855596502316039236
P2-Q2、P4-Q4 は 正弦定理より
B2 = B4 = (2/√3)sin(18゚) = (√5-1)/(2√3)
= 0.356822089773089931941969843046087873981686075246868366421
P3-Q3 は
B3 = tan(72゚)/2 -1/(2√3) - A
= (1/2)√(5+2√5) -1/(2√3) - A
= 0.477521162584205212885116485911137977764694599631516736273
したがって、ネットワークの長さは
2A + (2/√3) + B2 + B3 + B4 =
= 3.891156823326853818078262556719905049852981445670139299627728956 >>22 >>3 の出題者です, 遅くなりました.
私はlog2, log3を小数第4位までしか与えていないのですが, 其れは置いておきまして, 想定解は
11・9<100, 11⁵>160000
此等に常用対数を取って評価するものです.
>>64 >>57のほうが小さいよ。
前
>>57 最初は大きくなると思ってあきらめてました。が120°に注意して作図しなおしたら実際は小さくなりました。
左右非対称だというヒントにもかなっていると思います。
>>67 >>57の想定は間違っていると言う話をしている
つまり、角度を120°にしたとき、
2つの分岐点の距離と、分岐点から頂点への距離は異なる
同じと考えてそこから計算するのは間違い
>>3 20^(4/5) /10 = (8/5)^(1/5) < 11/10 < (4/3)^(1/3),
∴ (8/5)^(1/15)・(4/3)^(2/9) < 11/10 < (8/5)^(1/17)・(4/3)^(4/17),
∴ 1.04137216 < log(11) < 1.0414044
なお log(11) ≒ 1.041392685
x1,・・・,xn はすべてm以下の自然数
y1,・・・,ym はすべてn以下の自然数
このとき {xi|1≦i≦n},{yj|1≦j≦m} からそれぞれいくつかの数を選んで
それらの和が等しくなるようにできることを示せ
m=nの場合はある本に載ってた。
ほとんどそのままの論法でいけた。
>>73 > ある本に載ってた。
構わん、続けたまえ!
zi=z1+‥+zi、wj=y1+‥+yj とする。
zn≦wmとしてよい。
各1≦i≦nに対して
y j(i-1)<xi≦yj(i)
をみたすj(i)がとれる。
この時各iに対し0≦y(j(i))-xi≦n-1である。
=0が成立するiがあるときには、主張は正しいから≠0とする。
このときyj(1)~yj(n)は全て1~n-1であるから相異なるi1、i2でyj(i1)=yj(i2)となるものがとれる。以下ry
>>68圧倒的多数らしい右のハサミが大きい(左利き?)シオマネキのオスを、分岐点が正五角形の下方に水平に並ぶように描きました。
前
>>67分岐点の角度を120°にするという発想は当初なかったんですが、前スレの左右対称のカブトガニのような図を見て、(最小値は0.89……)分岐点については理にかなってると考えを改めざるをえませんでした。
左右非対称だというヒントで、シオマネキのオスの形を描きなおしました。
正五角形の中に正六角形の半分を描きます。シオマネキの胴体です。分岐点の角度を120°にしたということは正六角形なんで辺の長さは同じ。
分岐点と分岐点の距離は正五角形の対角線(正六角形を二分する線)の半分です。
分岐点から下方の頂点に引いた短い線は、右下か左下にこの短い線の正三角形ができるように平行線を描くことで、
(1-対角線の半分)
と直感しました。
∴1+(対角線の半分)×3+(1-対角線の半分)×2
=1+(3/4)(1+√5)(1/2)(3-√5)
=(13+√5)/4
>>75の後半ことごとくzとwがxとyになってる。
エスパーしてちょ
次の方程式が持つ整数解の個数は有限か、無限か。
1 + 3x^2 + 4y^3 - 108z^6 = 0
>>79 (x,y,z) = (0,3t^2,t)が解だから無限個。
>>55 a_n=a,b_n=b と略す。
{1,2,…,b} のb個のうち {a_k} に含まれるものの数は [(b+1)/√2] 個
{1,2,…,b-1} のb-1個のうち {a_k} に含まれるものの数は [b/√2] 個
∴ [b/√2] = [(b+1)/√2] = n-b,
n-b ≦ b/√2, (b+1)/√2 < n-b+1,
n - (1 -1/√2) < (1 -1/√2)b ≦ n,
(2+√2) を掛けると題意から
n(2+√2) -1 < b ≦ n(2+√2),
一方、定義から
-n√2 ≦ -a < -n√2 +1,
辺々たして
2n-1 < b-a < 2n+1
∴ b-a = 2n.
>>83 訂正
∴ [b/√2] = [(b+1)/√2] = b-n,
>>79 (|x|,y,|z|) = (5,2,1) (1,-1,0)
有限っぽい…
学部1~2年レベル置いとく
⑴V,Wを有限次元K線形空間とする。f:V→Wの基底ℬ,ℬ'に関する表現行列がAである時、fの双対f *の基底ℬ'*,ℬ*に関する表現行列を求めよ
⑵任意の対称形式b:V×V→Kに対し
て、Kの標数が2でなければ直交基底が存在する事を示せ
⑶L^p[0,1]をp乗可積分な関数全体とする。この時、||f||={∫[0,1]|f|^pdx}^(1/p)でノルムを入れる。このノルムによる単位球面S={f:||f||=1}はコンパクトではない事を示せ。
但し、ここでいう積分は全てリーマン積分で考える
1+3(6z^2-1)^2+4(3z^2-1)^3-108z^6=0。
>>87 正解です。
abc conjecture のちょっとした一般化に n conjecture なるものがあるのですが、
この式のzに何を代入しても良いことから、強い方の n conjecture の反例"に近いもの"(
すなわち和が0になるような整数の四つ組であって、どの二つ組の最大公約数も高々4であるもの)がいくらでも構成できます。
この最大公約数の最大を4から1にできないかなとは考えてるけどこれがなかなか難しい…
>>86 (3)正の整数nに対して f_n(x) の値を
2^n (2^(-n+1) - 2^(-pn) < x < 2^(-n+1) の時)
0 (それ以外)
と定めたら、f_n∈S かつ ||f_n-f_m||=2 となるので、
{f_n}_n=1,2,… のどの部分列も収束しない。
したがってSは点列コンパクトでないためコンパクトでない。
数値ちがう。
そもそも最小性の証明出来てないから話にならん。
aを1でない実数とする。
[tan(log|log√√√√‥√a|]
において√の数を変化させるとき上式は全ての実数値を取りうることを示せ。
>>92 え?これが出来たら自然数から実数への全射が出来ることにならない? 濃度に反するんだが
稠密の間違いじゃないの?
カッコが対応してないのも気になるが、
一番外側のカッコがガウス記号のつもりなら、「全ての実数値」は「全ての整数値」の間違いだったりするのかな?
>>93 ×すべての実数値
○すべての整数値
orz
>>79 1 + 3x^2 + (1/2)(x-1)^3 - (1/2)(x+1)^3 = 0,
1 + 3x^2 + 4{(x-1)/2}^3 - 108{(x+1)/6}^3 = 0,
>>92 >>95 a>0,a≠1,√がn個あるとする。
log|log(√√√√…√a)| = log|(1/2^n)log(a)|
= log|log(a)| - log(2^n)
= log|log(a)| - n・log(2),
これはnの等差数列である。
次は tan だから mod π で考えよう。
上式にπ/2 を加えてπで割った ( log|log(a)| - n・log(2) + π/2)/πの小数部分を c_n とおく。
任意の有限区間(α,β)内に或る c_n が存在することを示そう。
〔補題〕
0≦α<β≦1 に対し、α < c_n < β をみたす自然数nが存在する。
(略証)
[ 1/(β-α) ] + 1 = m とおくと、β-α > 1/m
鳩ノ巣原理により
c_1,c_2,…,c_{m+1} の中に |c_i - c_j| < 1/m となる i<j がある。
n を j-i ずつ増減すれば、c_n はある公差(<1/m)で増減する。
∴ m/2回以内にc_nは区間 (α,β) に到達し、補題が成立する。(終)
>>97 正解です。いろいろ問題文不備あったけどエスパーしていただいて申し訳ない。
問題は
an = -n (log2)/π + (log | loga |)/πの小数部
がどうなるか?
です。
用意した解答。
――
はLindemannの定理から(log2)/π は無理数。
https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%B3%E3%83%87%E3%83%9E%E3%83%B3%E3%81%AE%E5%AE%9A%E7%90%86 よってWeylの一様分布定理
http://integers.hatenablog.com/entry/2016/07/30/140137 により任意の0≦α<β≦1に対し
lim[n→∞] #{n | α < an < β} /n = 1/(β - α)
が成立することから主張が成立。
――
ホントは上のサイトで紹介されているKroneckerの定理でも証明できるのですが、なんといってもWeylの発見したワイルの基準(Weyl's criterion)が美しく素晴らしい。
はじめて見たときはちょっと感動しました。
>>98 訂正
× lim[n→∞] #{n | α < an < β} /n = 1/(β - α)
○ lim[N→∞] #{n | α < an < β , n≦N }/N = 1/(β - α)
>>97 鳩ノ巣原理のところを、
0 < |c_i - c_j| < 1/m となる i≠j がある。
と訂正。
Lindemann により log(2)/π が無理数だから。
カブトガニ型の左右対称な分岐点3つの経路の値を確認した。
(斜め線4つ)=(1+√5)/2×(2/√3)
=(1+√5)/√3
(短い縦線)=(正五角形の高さ)-(中央と左右の分岐点の水平距離)(1/√3)-(長い縦線)
=√[{(1+√5)/2}^2-(1/2)^2}]-1/2√3-(長い縦線)
(長い縦線)=(左右の頂点の高さ)-(左右の頂点と左右のの分岐点の水平距離)×(1/√3)
=√[1-{(1+√5)/4 -(1/2)}^2]-{(1+√5)/4 -(1/2)}(1/√3)
=(1/4)√(10+2√5)-(√5-1)/4√3
(最小値)=(1+√5)/√3+(1/2)√(5+2√5)-1/2√3+(1/4)√(10+2√5)-(√5-1)/4√3
=(1+2√5)/2√3+(1-√5)/4√3+(1/4)2√(5+2√5)+(1/4)√(10+2√5)
=(1/4){2√(5+2√5)+√(10+2√5)+(1+√5)√3}
≒(1/4)(6.15536707+3.80422607+5.60503415)
=3.89115682……
前
>>90 1-6, 2-5, 3-4が向かい合った, 1~6までの各数を揃えた6面サイコロを作る.
サイコロの1つの角c_nを共有する3面の数を合計した数をS_nとする.
(1)1つの角を共有する3面の数の組合せは何通り取れるか?
(2)S_nの最小値, 最大値を求めよ.
又サイコロを如何に作れど, S_nが最小値, 最大値を取る組み合わせの3面が必ず存在することを示せ.
>>102 (1) 8通り
(2) 8つの角に現れる数はいかなるサイコロでも8つの角それぞれの計は
1+2+3=6、 1+2+4=7、 1+5+3=9、 1+5+4=10、
6+2+3=11、6+2+4=12、6+5+3=14、6+5+4=15。
最小値は6,最大値は15。
>>103 正解です.
(ii)は鳩ノ巣原理使った解答想定していたけど, 8通りだと書き出す方が確かに早かった.
>>97 >>98 〔Kroneckerの稠密定理〕
c を無理数とする。
0≦α<β≦1 である任意の区間(α,β) に対して α< {nc} <β を満たす自然数nが存在する。
http://mathtrain.jp/kronecker a[1]=1/2
a[n+1]=a[n]/(1+a[n])^2
で与えられる数列について、
(1)極限値lim[n→∞] na[n] を求めよ。
(2)次の極限が0でない有限値に収束するような正の有理数pの値を求めよ。
lim[n→∞] {a[n]-(1/n)(a[1]+a[2]+...+a[n])}*(n^p)
>>106 (2)解無しになるんじゃないの?
(1)は数値実験で1/2っぽいけど、だとすると a[n] ~ 1/(2n) で (1/n)(a[1]+a[2]+...+a[n]) ~ (log n)/(2n) にならない?
>>107 (1)は確かに1/2だが証明を与えてほしい
(2)は解無しもありだが本当にそうなのかを説明してほしい
大学入試問題からヒントを得た問題だが高校生には難しすぎるだろうと思ってここに出してみた
(1)
lim a[n] = 0 は容易。
e>0 に対しa[n] < e (∀n ≧ N)であるNをとって
1/a[n+1] = 1/a[n] + 2 + a[n]
1/a[n] + 2 < 1/a[n+1] <1/a[n] + 2 + e
∴ 2(n - N) + 1/a[N] < 1/a[n] < (2+e)(n-N) + 1/a[N]
∴ 2 ≦ liminf 1/(na[n]) ≦ limsup 1/(na[n]) ≦ 2 + e
eは任意であったから主張は示された。
(2)
(1)と同様にe,Nをとって
Σ[k:N~n]1/((2+e)(n-N) + 1/a[N]) ≦ Σ[k:N~n]a[k] ≦ Σ[k:N~n] 1/((2+e)(n-N) + 1/a[N])
より
1/(2+e) ≦ liminf Σ[k:1~n]a[k]/log n ≦ limsup Σ[k:1~n]a[k]/log n ≦ 1/2
eは任意であったから
lim Σ[k:1~n]a[k]/log n = 1/2。
∴解無し。
R^nの凸集合A,Bについて,A⊂Bならば Aの境界の表面積≦Bの境界の表面積 となることを証明せよ
>>110 以下凸体Vに対しその表面積をS(V)と書く。
e>0をとる。
Aにふくまれる凸多面体A'でS(A)<S(A') + eなるものをとる。
A'の各面Fに対しFを底面とする柱で側面が底面と垂直であり、A'の外側に伸びるものをC_Fとする。
C_Fが切り取るBの表面をT_Fとする。
このとき
S(A) - e ≦ S(A') = Σ (Area of F) ≦ Σ (Area of T_F) ≦ S(B)。
eは任意であったから S(A) ≦ SI(B)。
>>111 なるほど
想定していた解答はガウスの発散定理を使うものでしたがこれでも完璧ですね
正解です
>>112 あざっす。想定解面白そう。教えて下さい。
>>109 訂正
(2)
e>0をとる。
(1)よりn≧Nにたいして(2-e)/n ≦ a[n] ≦ (2+e)/nを満たすNをとる。
Σ[i:1~N]a[i] = Sとおけば
S+(2-e)(log n - log N -1/n) ≦ Σ[i:1~n]a[i] ≦ S+(2+e)(log n - log N)。
2-e ≦ liminf Σ[i:1~n] a[i]/log n ≦ liminf Σ[i:1~n]a[i]/log n ≦ 2+e。
eは任意であったからlim Σ[i:1~n] a[i]/log n = 2。
∴解無し。
>>113 以下想定解答です
Aは滑らかとして十分(軟化などをする)
dを∂Aに対する符号付き距離関数,すなわち
d(x):=dist(x,∂A) (=inf{dist(x,y) | y∈∂A}) (x∈A) , -dist(x,∂A) (x∈A^c) とする
x∈∂Aのとき,∇d(x)は∂Aの外向き単位法線ベクトルとなる
また,∇・∇d(x)=△d(x)は∂Aの点xにおける平均曲率となる
また,Aは凸より,任意のt<0に対して,{x∈R^n | d(x)=t}も凸
滑らかな凸集合の平均曲率は正より,△d(x)≧0 (x∈A-B)
A⊂Bより,0≦∫_(B-A) △d(x) dx=∫_B △d(x)dx-∫_A △d(x)dx
ガウスの発散定理より n_S(x)をSの外向き単位法線べクトルとすれば,
∫_B △d(x)dx-∫_A △d(x)dx=∫_(∂B) ∇d(x)・n_(∂B)(x) dS-∫_(∂A) ∇d(x)・n_(∂A)(x) dS
≦S(∂B)-S(∂A) (∵∇d(x)・n_(∂A)(x)=n_(∂A)(x)・n_(∂A)(x)=1 (x∈∂A) ,∇d(x)・n_(∂B)(x)≦|∇d(x)||n_(∂B)(x)|≦1 (x∈∂B))
よってS(∂A)≦S(∂B)
>>116 なるへそ。
{x∈R^n | d(x)≦t}が凸。なので△d(x)≧0 (foy x not in A)。
こんなの成り立つのか。知らなんだ。面白い。
この
>>116 >∇・∇d(x)=△d(x)は∂Aの点xにおける平均曲率
とかの周辺の話って勉強できるおすすめの教科書ってありますか?
なるへそ。有向距離d(x)を
d(x) = (x~∂A の最短距離), x∈A
=-(x~∂A の最短距離), x∈A^c
= 0 x∈∂A
とおく。
∇d(x) = (∂Aの外向き法線単位ベクトル), x∈∂A
∇・∇d(x) = (∂Aの平均曲率), x∈∂A
等距離面 {x∈R^n | d(x)=t} も凸
滑らかで凸 ⇒ (∂Aの平均曲率) = ∇・∇d(x) ≧ 0, (x∈A でない)
こんなの成り立つのか。知らなんだ。面白い。
∂Aが滑らかで凸 ⇒ 等距離面も滑らかで凸 ⇒ (等距離面の平均曲率) = ∇・∇d(x) ≧ 0, (x∈A でない)
>>117 あーごめん間違いをエスパーしてくれてありがとう
そうだね{d≦t}とB-A上だね
>>118 うーんちょっと洋書で申し訳ないんだけど
Carlo MantegazzaのLecture Notes on Mean Curvature Flowなんかには詳しく載ってるよ
A:単位球(半径=1)
B_n:Aに外接する正n面体
とすると
S(∂A) = 4π,
S(∂B_4) = (√3)(L_4)^2 = 24√3, (L_4 = 2√6)
S(∂B_6) = 6(L_6)^2 = 24, (L_6 = 2)
S(∂B_8) = (2√3)(L_8)^2 = 12√3 = 20.7846097 (L_8 = √6)
S(∂B_12) = 3√(25+10√5)(L_12)^2 = 16.650873 (L_12 = 0.898056)
S(∂B_20) = (5√3)(L_20)^2 = (60√3)/φ^4 = 15.16216843 (L_20 = (2√3)/φ^2 = 1.323169)
π < 3.7905421
>>124 単位円と、それに外接する正n角形の面積を比べた方がいいな…
n=6 正6角形
π < 6 tan(π/6) = 2√3 = 3.4641016
n=8 正8角形
π < 8 tan(π/8) = 8(√2 -1) = 3.3137085
n=12 正12角形
π < 12tan(π/12) = 12(2-√3) = 3.2153903
球に外接する多面体のデータなら前スレ642にあるな
数値の信憑性は定かではないが……。
女体信仰から始まったのか?モノに執着もあるし、怖い自然もある。異種と出会うこともまれながら、愛した思い出もある。
円に内接する正三角形ABCと劣弧AB上の点PについてAP+BP=CPを示せ。

>>129 トレミーの定理より
AP・BC + BP・AC = CP・AB。
∴ AP+BP=CP。
>>130 正解(想定解)
>>131 正三角形CPDを描くと、∠CPB=∠CAB=∠60°だからBは辺PD上
二辺夾角相等より△CAP≡△CBD
AP+BP=BD+BP=DP=CP
正解
別スレで出題したのですがこちらの方が適当かなと思いまして、こちらで出題します。
「問題」
2つの円CとDは相異なる2点で交わっている。これによりCとDの和集合である領域は、CおよびDの円弧により3つの領域に分割される。
すなわち、
Cの内部かつDの外部である領域P、
Cの内部かつDの内部である領域Q、
Cの外部かつDの内部である領域R、
に分割される。
このとき、CとDがどのような交わり方をしていても、次の(条件)を満たすような直線lが必ず存在するか。
(条件)
・lは領域P、Q、Rのどの内部も通る。
・lの領域Kに含まれる部分の長さをL[K]とおくとき、次の等式が成り立つ。
L[P]=L[Q]=L[R]
いくつかの赤玉と白玉の入った袋がある。
以下の試行(T)を繰り返す
(T) : 無作為に玉を一つ取り出し赤玉ならその玉と白玉一個を追加して袋にもどし、白玉ならそのまま取り除く。
この試行をn回行った後の白玉の個数をXnとする。
最初赤玉a個の状態であったとしてlim[n→∞] E(Xn)を求めよ。
――
別スレの問題を改題。
とりあえずいろいろ収束すると仮定すればlim[n→∞] E(Xn)はさらっと求まりますが、収束証明が難しい。
私、出来なくて知ってる限りのそ関連ありそうな単語でいろいろググったらやっと出きた。
>>134 訂正
最初赤玉a個の状態であったとしてlim[n→∞] E(Xn)+ E(X(n+1))を求めよ。
>>134 赤玉の個数は永遠に変わらないa個のまま
Xnの時点で
赤がでる確率a/(Xn+a)
Xn+1=Xn+1
白がでる確率Xn/(Xn+a)
Xn+1=Xn-1
E=lim E(Xn)が存在すれば
E=(E+1)a/(E+a)+(E-1)E/(E+a)=(E^2+(a-1)E+a)/(E+a)=E-(E-a)/(E+a)
E=a
>>134 最初の時点での白玉の個数をb個とする
n回の試行中x回赤玉がy回白玉がでているときn=x+yで
Xn=b+x-y
しかし
(x,y)→(x+1,y)と遷移する確率はa/(a+b+x-y)
(x,y)→(x,y+1)と遷移する確率は(b+x-y)/(a+b+x-y)
Xn≧0よりy≦x+b
またもちろん0≦x,y
n次行列値関数 A(t)、B(t) が、dA(t)/dt = A(t)B(t)-B(t)A(t) をみたすとき、
tr(A^k) はtに依らない定数であることを示せ。ただしkは自然数とする。
>>134 数値実験結果(赤玉3個、白玉0個から始めた場合の n :1001~1010の E(Xn))。
http://codepad.org/TRA2Qa3r 1001 : 6.501239
1002 : 6.498761
1003 : 6.501239
1004 : 6.498761
1005 : 6.501239
1006 : 6.498761
1007 : 6.501239
1008 : 6.498761
1009 : 6.501239
1010 : 6.498761
>>138 dA(t)/dt = A(t)B(t)-B(t)A(t)
の両辺のtraceをとって
d/dt trA(t) = tr (A(t)B(t)-B(t)A(t)) = 0。
>>140 訂正。
これは玉の総数の期待値。つまりE(赤玉の個数+X_n)でした。
>>138 dA(t)/dt = A(t)B(t) - B(t)A(t),
d/dt {A(t)^k} = Σ[j=1,k] A(t)^(j-1) {A(t)B(t) - B(t)A(t)} A(t)^(k-j)
= Σ[j=1,k] A(t)^j・B(t)・A(t)^(k-j) - A(t)^(j-1)・B(t)・A(t)^(k+1-j)
= A(t)^k・B(t) - B(t)・A(t)^k,
∴ 任意の多項式 P(x) について
d/dt P(A(t)) = P(A(t))B(t) - B(t)P(A(t)),
∴ tr{P(A(t))} は一定。
〔問題670〕
nを自然数、xを実数とするとき
[nx] ≧ Σ(k=1,n) [kx]/k
を示せ。ただし [x] はガウス記号である。
[前スレ.670,680+684+717]
>>144
[a+b] = [a] + [b] + [{a}+{b}] ≧ [a] + [b],
j≧2 のとき
S_j = (j-1)・[jx] - 2Σ(k=1,j-1) [kx]
= Σ(k=1,j-1) ( [jx] - [kx] - [(j-k)x] )
≧ 0,
f(x) = [nx] - Σ(k=1,n) [kx]/k
= Σ(j=2,n-1) (1/j - 1/(j+1))・S_j + (1/n)・S_n
≧ 0, g:ℤ →ℤとして,
∀n; g(g(g(g(n))))=2n
を満足するg(n)を挙げよ.
gは一意的だろうか.
f=gg
ffn=2n
f2n=fffn=2fn
f(2n+1)を任意に選ぶと
f2^k(2n+1)=2^kf(2n+1)
gg2^k(2n+1)=2^kgg(2n+1)
>>146 奇素数pを任意に固定する。
f(0)=0 とし、 0 でない整数 n = m・p^k (mはpと互いに素な整数) に対して f(n) の値を
2n/(p^3) (kが4で割って3余る時)
pn (それ以外)
と定めれば、f は満たすべき性質を満たす。
また、奇素数 p は任意であったから、一意的ではない。
>>146 Sを1と素数の集合し、S=∪Tiを4元ずつのdisjoint unionとする。T={a,b,c,d}をそのうちの一つとして
f(a2^i)=b2^i、f(b2^i)=c2^i、f(c2^i)=d2^i、f(d2^i)=a2^(I+1)、f(0)=0
とすれば良い。
0337 卵の名無しさん 2018/08/12 08:03:01
数学板にあった問題をこのスレの趣旨に合わせて改変。
あるド底辺シリツ医に
学力考査で入学した学生(学力学生)と任意の寄付や縁故による加点で入学した学生(裏口学生)がいるとする。
無作為に一人選んで調査して以下の「浄化操作」をする。
・調査対象の学生が裏口学生なら退学させる。
・調査対象の学力学生ならそのまま在籍させて裏口学生を一人追加入学させる。
この「浄化操作」を n 回行った後の裏口学生の人数を Un とする。
最初に学力学生10人、裏口学生90人がいるとしてn→∞としたときの Un の期待値を求めよ。
>>141 意味不明。
>>143 > = Σ[j=1,k] A(t)^j・B(t)・A(t)^(k-j) - A(t)^(j-1)・B(t)・A(t)^(k+1-j)
> = A(t)^k・B(t) - B(t)・A(t)^k,
一般にA(t)とB(t)は可換でない。
>>147 一瞬グラフみて「え?10.5近辺に収束するはずなんだけど」と思ってあせりました。
グラフ下の方切れてるんですね。
赤10,白90からスタートした場合のCでの数値実験。
http://codepad.org/ALVNXu5t ――
1001 : 10.500000
1002 : 10.500000
1003 : 10.500000
1004 : 10.500000
1005 : 10.500000
1006 : 10.500000
1007 : 10.500000
1008 : 10.500000
1009 : 10.500000
1010 : 10.500000
――
ちなみに収束してるようにみえますが±1/(2 exp 20)の幅で奇数項と偶数項で振動するはずです。
しかし奇数項+偶数項は収束します。
収束性を仮定すると赤10の場合なぜ奇数項+偶数項が21に収束するかは割と簡単に示せると思います。
>>154 (下)
意味不明。
(t) を略して書くと、
= Σ[j=1,k] {A^j・B・A^(k-j) - A^(j-1)・B・A^(k+1-j)}
= {A^k・B - A^(k-1)・BA} + {A^(k-1)・BA - A^(k-2)・BAA} + ……
+ {AAB・A^(k-2) - AB・A^(k-1)} + {AB・A^(k-1) - B・A^k}
= A^k・B - B・A^k,
一般にA(t)とB(t)は可換でない。
(1)
d/dt tr A(t) = tr d/dt A(t)
を示せ。
(2)
tr AB = tr BA
を示せ。
>>135 EXn+EXn+1は振動しない?
EX2n+E2n+1とかではなくて?
>>159 振動しません。
十分大きいnでは
……x,y,x,y,x,y,x,y……
のような形になるので。
振動幅ごくわずかですけど。
もっというなら各 i に対し
lim P(X_{2n-1} = i)、lim P(X_{2n} = i)
はすべて収束します。
それを使えば
>>135 の答えは割と簡単。
問題は収束性。
ネットで調べまくって、いや~偉い人は偉いなぁとしみじみ思いました。
行列の成分表示を使わない trace って、どう定義されるんだっけ?
つまり、-(固有値の総和)のことなんだけど、これを一次変換の変換の性質を表す言葉を使った定義。
>>161 射影変換の場合はその階数だと思うけど…
一般の場合はどうするか?
数列{a[n]}は上に有界かつ単調増加である。
この数列の極限値をαとするとき、同じ極限値に収束する定数でない数列{b[n]}で、以下の性質を持つものを考える。
(A)ある自然数kが存在し、m>kであるすべての自然数mに対して、|b[m]-α| < |a[m]-α| が成り立つ。
(B)ある2次多項式f(x)が存在し(2次の係数は0でない)、b[n]=f(a[n])と表される。
(1)性質(A)を持つ{b(n)}が存在することを示せ。
(2)性質(A),(B)をいずれも持つような{b(n)}は存在するか。
>>155 これは lim[n→∞] E(Xn)のグラフ。
>>163 ・f(α) = α
・a1≦x<αにおいてfは単調増加、x<f(x)<α
であるfをとれば良い。
>>155 赤10,白90からスタートして
n回試行後のXnの期待値X[n]は
X[0]=90
red=10
X[i+1] = (X[i] +1)*red/(X[i]+red) + (X[i] - 1)*X[i]/(X[i]+red)
で10に収束するように思えるんだけど。
> Xn <- function(n,red=10,white=90){
+ X=numeric()
+ X[1]=white
+ for(i in 1:n){
+ X[i+1] = (X[i] +1)*red/(X[i]+red) + (X[i] - 1)*X[i]/(X[i]+red)
+ }
+ return(X[n+1])
+ }
> sapply(c(100,200,300,400,500),Xn)
[1] 24.22034 10.17547 10.00105 10.00001 10.00000
>>166 その漸化式がおかしい。
X(0) = 90、X(1) = 992/10
までは正しくでるけどその漸化式では
X(2) = 54809 / 620。
でも正しくは
P(2回目で玉98個) = 89/110、
P(2回目で玉100個) = 2011/1111、
P(2回目で玉102個) = 1/101
なので
X(2) = 546621/5555。
訂正
P(2回目で玉100個) = 2011/11110、
>>145
[nx] - Σ(k=1,n) [kx]/k = Σ(j=2,n) c_j・S_j
とおく。c_2 ~ c_n は定数。
まず [nx] を含むのは S_n だけ。
1 - 1/n = (n-1)c_n,
c_n = 1/n,
次に [(n-1)x] を含むのは S_n と S_{n-1}.
-1/(n-1) = (n-2)c_{n-1} - 2c_n,
c_{n-1} = 1/(n-1) - 1/n,
さらに [jx] を含むのは S_n ~ S_j.
-1/j = (j-1)c_j - 2(c_{j+1} + … + c_n)
= (j-1)c_j - 2/(j+1),
c_j = 1/j - 1/(j+1), (2≦j<n) >>148 >f2^k(2n+1)=2^kf(2n+1)
ff(2n+1)=2(2n+1)
f(2n+1)=2^k(2m+1)とすると
ff(2n+1)=f2^k(2m+1)=2^kf(2m+1)=2(2n+1)より
k=1,f(2m+1)=2n+1
または
k=0,f(2m+1)=2(2n+1)
そこで
A={2m+1|f(2m+1)が奇数}
B={2n+1|f(2n+1)が奇数の2倍}
と定めるとABは可算集合ですべての奇数はどちらか一方のみに所属
逆に奇数をどちらも可算のA,Bに分けて
h:A→B:isoを任意に取り
2m+1∈Aに対してf(2m+1)=h(2m+1)=2n+1,f(2n+1)=2(2m+1)と定義し2べき倍に拡張すれば
fは所定の性質ffn=2nを持つ
しかし
gg(2n+1)=2(2m+1)
gg(2m+1)=2n+1
および
gg2n=2ggn
>>168 ご指摘通り、
2回めが赤でも
1回めが赤で2回めが赤の場合と
1回めが白で2回めが赤の場合で
期待値は異なりますね
御助言ありがとうございました。
>>168 X(n)は球の総数として
P(2回目で玉100個) になるのは99→100の場合と101→100の場合があって
前者は90/100*10/99、後者は10/100*91/101で異なりますね。
御指摘に従ってコードを書き直しました。
X <- function(n,red=10,white=90){
rw=red+white
p=list()
total=list()
total[[1]]=c(rw-1,rw+1)
p[[1]]=c(white/rw,red/rw)
if(n > 1){
for(i in 1:n){
total[[i+1]]=c(total[[i]]-1,total[[i]]+1)
p[[i+1]]=c(p[[i]]*(total[[i]]-red)/total[[i]], p[[i]]*red/total[[i]])
}
}
return(sum(p[[n]]*total[[n]]))
}
計算結果は合致しました。
> X(2)
[1] 98.40162
> 546621/5555
[1] 98.40162
プログラムとしては間違っていないと思うのですが、メモリー不足になって実用性はありませんでした。
f:R^2→R が原点で連続ならば
lim(x→0)lim(y→0)f(x,y)=lim(y→0)lim(x→0)f(x,y)
は成り立つか?
>>140
省エネ化してRに移植
# 確率を行列化
rm(list=ls())
X = function(n,r=10,w=90){
# s[i,j]
rw=r+w # 試行前総玉数
J=rw+n # jの上限
s=matrix(0,nrow=n,ncol=J) # i回試行後に総数がj個である確率の行列
s[1,rw-1]=w/rw ; s[1,rw+1]=r/rw # 1回試行後
if(n > 1){
for(i in 2:n){
for(j in r:J){ # jはr未満にはならない
# if(j==1) s[i,j] = s[i-1,j+1]*(j+1-r)/(j+1)
if(j==J) s[i,j] = s[i-1,j-1] * r/(j-1)
else s[i,j] = s[i-1,j-1] * r/(j-1) + s[i-1,j+1]*(j+1-r)/(j+1)
}
}
}
total=sum((r:J)*s[n,r:J])
white=total-r
return(c(total=total,white=white))
}
X(2)
546621/5555
vX=Vectorize(X)
vX(1000:1010)
> vX=Vectorize(X)
> vX(1000:1010)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
total 20.5 20.5 20.5 20.5 20.5 20.5 20.5 20.5 20.5 20.5 20.5
white 10.5 10.5 10.5 10.5 10.5 10.5 10.5 10.5 10.5 10.5 10.5 >>175 例えば f(x,y) の値を
|x| (x,yがどちらか一方のみが有理数の時)
0 (それ以外の時)
と定めればfは原点で連続であるが、x≠0 の時に lim(y→0)f(x,y) は定義されないため、二行目の等式が成り立つことはない。
{n}=1111...111と定義する(nは自然数であり、10進法表記したときに1がn個並んでいる)。
(1){n}=3^a(aは自然数)となることはあるか。
さらに、自然数kおよび非負整数mに対し、以下の等式を満たす非負整数a及び整数b(bは1または2である)がただ1つに定まるとき、a,bを決定せよ。
ただ1つに定まらない場合はaの最大値を述べよ。
ただしaは非負であり、bは1または2とする。
(A){3k}=(3^a)*(3m+b)
(B){3(k+1)}=(3^a)*(3m+b)
(C){3(k+2)}=(3^a)*(3m+b)
>>167 1000~1010回試行をそれぞれ100回繰り返して平均をだすシミュレーション結果で10.5近辺で振動したから
シミュレーションのコードは正しいと思う。

>>150-151 で
奇数m、(m,p)=1、非負整数j≧0 に対し
T_(m,j) = {m・p^(4j),m・p^(4j+1),m・p^(4j+2),m・p^(4j+3)} = {a,b,c,d}
としたものが
>>149 >>140 精度上げて計算。
赤10,白90スタート。
http://codepad.org/d3B4hPPi 1001 : 0000020.50000000103057681723857863179375573
1002 : 0000020.49999999896942319451989818931917708
1003 : 0000020.50000000103057681669136956653754163
1004 : 0000020.49999999896942319399815481629102060
1005 : 0000020.50000000103057681619390677994098141
1006 : 0000020.49999999896942319352384265899269428
1007 : 0000020.50000000103057681574166788303501812
1008 : 0000020.49999999896942319309264978872148864
1009 : 0000020.50000000103057681533054161312050221
1010 : 0000020.49999999896942319270065627029311700
>>176 Rは16桁が限度
> print(data.frame(total),digits=16)
total
1001 20.50000000103054
1002 20.49999999896938
1003 20.50000000103054
1004 20.49999999896938
1005 20.50000000103054
1006 20.49999999896938
1007 20.50000000103054
1008 20.49999999896938
1009 20.50000000103054
1010 20.49999999896938
丁度4個の元から成る, 乗法単位元を持つ可換とも限らない環R=({0,1,x,y},+,×)の演算表を以下に4つ作った.
但し, (1)~(4)で定義される環は互いに同型でないとし, 加法単位元を0, 乗法単位元を1と書いた.
表の残りを埋め, (1)~(4)の環構造を決定せよ.

>>183 4元からなる代数をRとしてk={1,1+1,…}のなす環はZ/2Z、Z/4Zのいずれか。
後者のときはR=Z/4Z。
kが2元体のときt∈R\kをとってR=k[t]はk上の2次元の代数で可換。
Rが零因子を持たないときはRは4元体。
Rが冪零根基をもつときはRはk[x]/(x^2)、持たないときはkΠk。
(2)はkが2元体でないのでZ/4Z。
(4)は残り3つのうちy^2=yがkの元でない解をもつのでkΠk。
(3)は残り2つのうちx^2がkの元でないのでF4。
(1)は残りのひとつk[x]/(x^2)。
整数から複素数への写像 f であって、次を満たすものはいくつ存在するか:
任意の整数 x, y について f(xy+1) = f(x+y) + f(x)f(y) が成り立つ。
高添沼田(葛飾区青戸6-23-21ハイツニュー青戸103号室)の挑発
高添沼田の親父「関東連合文句があったらいつでも孫を金属バットで殴り殺しに来やがれっ!! 関東連合の糞野郎どもは俺様がぶちのめしてやるぜっ!! 賞金をやるからいつでもかかって来いっ!!糞バエ関東連合どもっ!! 待ってるぜっ!!」 (挑戦状)
>>185 f(x) = 0, x-1, xx-1,
3つ以上
>>178 (1)
{n} = (10^n - 1)/9,
(解1)
nの素因数をpとすると
{p} | {n}
p=2 のとき
{p} = 11、{n}は11の倍数。
p=3 のとき
{p} = 111 = 3・37、{n}は37の倍数。
p>3 のとき
{p} = Σ[k=0,p-1] 10^k ≡ Σ[k=0,p-1] 1 = p ≠ 0 (mod 3)
∴ 3以外の素因数をもつ。
(解2)
題意より
10^n - 3^(a+2) = 1
n=1 のとき
a=0 となり不適。
n≧2 のとき
カタラン予想(ミハイレスクの定理)により、等式は成り立たない。
2直線l,mに対してsl+tmで表される直線は確かにl,mの交点を通る直線だが、逆にl,mの交点を通る直線は全て上の形で表されることを初等的に示せ。
(集合っぽくで書けば{sl+tm|s,t:実数}⊂{l,mの交点を通る直線全体}は成り立つが逆向きの包含関係は成り立つことを示せ。)
例えば:
2直線l,mの交点をPとし、各々の方向ベクトルをa,bとする。Pを通る任意の直線l'に対し、l,mは一点で交わるのでa,bは一次独立。l'の方向ベクトルcに対しある実数s,tが存在しc=sa+tbと表せる。このs,tに対しsl+tmで表せる直線を考えればこれはl'と一致している。
初等的とは、高校レベルです
Hilbertの零点定理などはやめてください。
背景としては、2直線の交点を通る任意の直線は2直線の(陰関数表示の)実数倍の和で表せる、みたいなことを使った問題を見ました。(つまり逆を使ってる)これって初等的に簡単に示せるのか?というものです
方向ベクトル使うのは良さそうですが、さすがにこれだけだと方向ベクトルの線型結合であって多項式の線型結合ではないけど続ければいけるかな。
0,1,2から無作為に1つの数字を選び、それを左から順に並べたものをa[1],a[2],...,a[n]とする。
このとき、1の位が0で、小数点以下第1位から順にこれらの数を並べ実数
0.a[1]a[2]a[3]...
を作る。このとき以下の確率を求めよ。
P( 1/9 < lim[n→∞] 0.a[1]a[2]a[3]... a[n] < 11/54)
f(a,b)g(x,y)-g(a,b)f(x,y)=0は(a,b)を通る。
2018×2019×2020×2021+aが平方数となるような最小の自然数aを求めよ
>>197 n(n+1)(n+2)(n+3)+1=(nn+3n+1)^2
>>192 簡単なことをある一定レベルの表記で書けと言う問題は
数学じゃないよ
いいかげん自然数という用語を廃止した方が良いと思う
>>197 平成31年て四か月だけあるのかな?
2018×2019×2020×2021+a=(2019-1)×2019×2020×(2020+1)+a
=(2019^2-2019)×(2020^2+2020)+a
=(2019×2020)^2-2020・2019・2020+2019・2019・2020-2019・2020+a
=(2019×2020)^2-2・2019・2020+a
a=2・2019・2020
=8076000+80760
=8156760
>>204 なんで既に答えが出てる問題のしかも間違って答えわざわざのせるん?
前
>>204 2018×2019×2020×2021+a=2018×(2018+1)×(2018+2)×(2018+3)+a
=(2018^2+3・2018)(2018^2+3・2018+2)+a
=(2018^2+3・2018+b)^2
(2+9)2018^2+6・2018+a=(2b+9)2018^2+6b・2018+b^2
b=1
∴a=b^2=1
あってるような。違うかも。
>>185の答え:7つ。
f(xy+1) = f(x+y) + f(x)f(y) …[0]
x=y=1 とすれば f(1)=0.
x=y=0 とすれば f(0)=0,-1.
f(0)=0 の場合、[0]において y=0 とすれば f(x)=0 が導けるので、以降 f(0)=-1 と仮定する。
y=-1 とすると、 f(-x+1) = f(x-1) + f(x)f(-1). …[1]
この x を 2-x に置き換えれば
f(x-1) = f(1-x) + f(2-x)f(-1).
足しあわせて
f(-1)(f(x)+f(2-x))=0.
(i) f(-1)≠0 の時
f(x)+f(2-x)=0. (特に、f(2)=1.)
これと [1] より f(x+1) + f(-1)f(x) + f(x-1) = 0.
これは三項間漸化式であり、f(0)=-1, f(1)=0 は決定されているので、関数fはf(-1)=:aの値で全て決まる。漸化式より、 f(-2) = 1 - a^2,
f(-3) = a^3 - 2a.
[0] で x=2, y=-2 とすれば、 f(-3) = -1 + f(-2) となるので、
a^3 + a^2 - 2a = 0.
a≠0 より、 a=1,-2.
これに対応するfはそれぞれ
f(x)=(xmod3)-1, (ただしxmod3はxを3で割った余り。以降同様)
f(x)=x-1
となるが、このどちらも[0]を満たす。
(ii)f(-1)=0 の時
[1]よりfは偶関数となるので、
f(m)= f(2m-3) - f(m-2)f(2) ([0]において x=m-2, y=2)
= f(-2m+3) - f(m-2)f(2)
= f(m-3) + f(m-1)f(2) - f(m-2)f(2). (x=m-1, y=-2)
これは四項間漸化式であり、 f(-1)=f(1)=0, f(0)=-1 は全て決定されているので、関数fはf(2)=:bの値で全て決まる。
漸化式よりf(3) = b^2 - 1,
f(4) = b^3 - b^2 - b,
f(5) = b^4 - 2b^3 - b^2 + 2b.
また、[0]でx=y=2を代入すると f(5)=f(4)+b^2 となるから、bについて解くと b=3,1,0,-1 となる。これに対応するfはそれぞれ
f(x)=x^2-1,
f(x)=-cos(πx/2),
f(x)=(x^2 mod3)-1,
f(x)=(xmod2)-1
となり、このいずれも[0]を満たす。
以上より、求めるfの個数は7つである。
>>209 そうです、ごめんなさいオリジナルなんです
最近数オリとかの関数方程式にはまってて自分も何か作ってみようかと思って色々いじってたら、
整数値しかとれない制約をつけた時に思いの外難易度が上がったので、試しにと思いついた二乗関連の恒等式から1つ作ってみたものです
問題をコピペしてくるしか能が無い出題者は悔い改めて(クソデカブーメラン)
連続した2018個の正整数の和として表され、かつ連続した2018個の正整数の積としても表される整数は存在するか。
>>213存在しないんじゃないの。前
>>206 和より積のほうが圧倒的に大きい。
1+2+3+……+2018=2019×1009=2019000+18171=2037171<1000・1001・1002<1・2・3・……・2018
2+3+……+2018+2019=2021×1009=2021000+18189=2039189<1001・1002・1003<2・3・……・2019
和より積のほうが圧倒的に大きい。宇宙のように膨張する。
>>203 自然数という用語が問題なのではなく、平然と拡大解釈(誤用)して改めない人たちが問題では?(特に一部の某基礎論…)
>>207 それで用は足りますね。
>>213 連続した2018個の正整数の和は、1009個の奇数を含むから、奇数。
連続した2018個の正整数の積は偶数。
空間において次の不等式を満たす点(x,y,z)全体からなる領域の体積を求めよ。
8≦(1+x^2)(1+y^2)(1+z^2)≦125
>>216 0≦x、0≦y、0≦zの領域の体積を8倍する。
キッチンのコーナーからゴキブリが顔を出すぐらいのスペースをあけてモルタルを満遍なくなめらかに塗るか蜘蛛の巣を張るイメージ。
y=0のとき、
(7-x^2)/(1+x^2)≦z^2≦(124-x^2)/(1+x^2)
x軸、y軸、z軸近辺は、√7から2√31の領域が題意を満たす。
点(1,1,1)と点(2,2,2)のあいだの領域が題意を満たす。
y=tのとき、
(7-x^2)/(1+t^2)(1+x^2)≦z^2≦(124-x^2)/(1+t^2)(1+x^2)
今0≦zなので、
√{(7-x^2)/(1+t^2)(1+x^2)}≦z≦√{(124-x^2)/(1+t^2)(1+x^2)}
lim(t=0→∞)Σ(x=0~∞)√{(124-x^2)/(1+t^2)(1+x^2)}-√{(7-x^2)/(1+t^2)(1+x^2)}
パス。
>>218 K(a) = {(1+x^2)(1+y^2)(1+z^2)≦a}、R(a,t) = K(a) ∩ {z=t}
とおく。
Area of R(a,t)
= Area of {(1+x^2)(1+y^2) ≦ a/(1+t^2)}
= Area of {1+r^2 + (1/4)r^2sin 2θ ≦ a/(1+t^2)}
= (a/(1+t^2) - 1)/2∫[θ]1/(1+(1/4)sin2θ)dθ
= 2π(a/(1+t^2) - 1)/√5
∴ Vokume of V(a) = 2∫[0,√(a-1)] 2π(a/(1+t^2) - 1)/√5 dt = …
∴ V(125) - V(8) = …
>>214 2組の「連続した2018個の正整数」が同じとは限らないよ。
>>218 (1+xx)(1+yy)
= 1 + rr + (xy)^2
= 1 + rr + {(1/2)rr sin(2θ)}^2
= 1 + rr + (1/8)r^4 {1-cos(4θ)},
>>198 n(n+3) = (nn+3n+1) - 1,
(n+1)(n+2) = (nn+3n+1) + 1,
辺々掛ける
>>220 下
撤回
>>208 >>210 7つとも実の整数解。(とくに周期解は {-1,0,1}のどれか)
複素数を持ち出す理由ないんぢゃね?
>>194 今回はl,mの交点Pを通る任意の直線がlとmの定数倍の和で表せる事を示したいです。つまりPを通る任意の直線l'に対してある実数s,tが存在してl'=sl+tmとなる事を示せば良いです。
なのでまずPを通る任意の直線l'を一つとってきてl'=sl+tmを満たす実数s,tの存在を示す…というのがオーソドックスな解法だと私は思いました
>>218
a/(1+tt) = 1+1/kk (k>0) とおくと
Area of R(a,t)
= Area of {(1+xx)(1+yy) ≦ 1+1/kk }
= 4∫[0,1/k] √{(1+1/kk)/(1+xx) - 1} dx
= -i(4/k) E(i・arcsinh(1/k) ; -kk)
= -i(4/k) E(i・log[1/k + √(1+1/kk)] ; -kk)
= ?
ここに
E(φ ; kk) = ∫[0,φ] √{1 - kk・(sinθ)^2} dθ
は第二種の楕円積分
E(iφ ; -kk) = i∫[0,φ] √{1 + kk・(sin(iθ))^2} dθ
= i∫[0,φ] √{1 - kk・(sinhθ)^2} dθ >>216 の近似値
V(125) = 479.6672
V(8) = 33.6566
V(125) - V(8) = 446.0106
>>223 まず、等式 l'=sl+tm が何を表す式なのかをはっきりさせないと、誰も答えてくれないだろう。
(1){}内はある無限小数において循環する部分を表す。0.{14159}を互いに素な正整数p,qを用いてq/pの形で表せ。
またその場合のpの桁数Nを求めよ。
(2)分母がN桁の整数である既約分数全体の集合をSとする。Sの要素で|3+r-π|を最小にする有理数rは(1)のq/pかどうか判定せよ。π=3.14159265358979...は既知としてよい。
Prelude Data.Ratio> (atan 1)*4 - (fromRational $ 208341 % 66317)
1.2235634727630895e-10
>>227 (1) p=99999,q=14159,N=5
(2) 3+(q/p)-π= -1.237675634×10^(-6)
行列の指数関数に対して、以下は成り立つか?成り立たないなら反例を挙げよ。
(1) e^A e^B = e^B e^A ならば、AB = BA.
(2) e^A e^B = e^B e^A ならば、e^(A+B) = e^A e^B.
0.1415926535…を連分数展開すると
[0;7,15,1,292,1,1,1,2,…]
深いところで打ち切るほど、より近似的な規約分数を与える
[0;7,15,1]=16/113=0.1415929…
[0;7,15,1,292]=4687/33102=0.1415926530…
[0;7,15,1,292,1]=4703/33215=0.1415926539…
[0;7,15,1,292,1,1]=9390/66317=0.1415926534…
[0;7,15,1,292,1,1,1]=14093/99532=0.1415926536…
[0;7,15,1,292,1,1,1,2]=37576/265381=0.141592653581…
特に|3+14093/99532-π|=2.9…*10^-11
>>231 素晴らしい解答です。14159/99999から平均を使って一回だけ近似する方法を考えていましたが、鮮やかです。
3 + 14159/99999 - π = -1.23767563409687122747・10^(-6) >>229
3 + 9390/66317 - π = -1.22356532942188597930・10^(-10) >>228
3 + 14093/99532 - π = 2.91433849348569181311・10^(-11) >>231 円周率の近似値として355/113より誤差が小さい分数の中で、最も分母が小さいものは何か?
*Main> sort [(b,a,abs $ pi - a/b) | a<-[1..400],b<-[1..113],(abs $ pi-a/b) <= (abs $ pi - 355/113)]
[(113.0,355.0,2.667641894049666e-7)]
3 + 16/113 - π = 2.667641890624223・10^(-7)
3 + 4495/31746 - π = -1.1997151645821・10^(-8)
3 + 4703/33215 -π = 3.3162780624607・10^(-10)
>>236 99733/31746 ではありません。
34906585/11111111
≒3.14159268
π≒3.14159265
前
>>238 ! Fortran 95
program pi
implicit none
integer :: p,q
real(8) :: a,b,r,s
a=dacos(-1D0)
b=dabs(a-355D0/113D0)
do p=1,40000
do q=1,p
r=3D0+dble(q)/dble(p)
s=dabs(a-r)
if (s<b) then
write(*,*) 3*p+q,"/",p,"=",r,s
stop
end if
end do
end do
stop
end program pi
52163 / 16604 = 3.1415923873765359 2.6621325721620792E-007
>>241 正解
分母がkの分数で、値がπに最も近いものは、[kπ]/k か [kπ+1]/k のどちらか。([x]はガウス記号)
kを1から変化させながら、この近似分数を発生させ、誤差を計る。
最小誤差が更新したときに、出力するようにしたのが、次のプログラム。
http://codepad.org/uDLvmZr4 出力結果から分かるように、 52163/16604 が答。
355/113 が桁数のわりに異常に精度が高いことが確認できると思う。
>>234 2π-355/113から355/113の間にある分数を虱潰しに探させて最初に見つかった分数を出してみた。
options(digits=16)
a=355
b=113
(U=a/b) # 3.141592 92
(L=2*pi-a/b) # 3.141592 39
f <- function(n){
m=0
x=m/n
while(x<U){
if(L<x) return(m-1)
x=m/n
m=m+1
}
return(NULL)
}
n=1
while(is.null(f(n))){
if( !is.null(f(n)) ) break
n=n+1
}
cat(f(n),'/',n,'\n')
f(n)/n
> cat(f(n),'/',n,'\n')
52163 / 16604
> f(n)/n
[1] 3.141592387376536
3 + 16/113 - π = 2.667641890624223・10^(-7)
3 + 2351/16604 - π = -2.6621325746395047764・10^(-7)
相加平均すると
3 + 531327/(2・113・16604) - π = 2.75465799235917364424・10^(-10)
>>242 正解の出し方ありがとうございました。
Rにはガウス記号にあたるfloorという関数があるのでこれでやってみました。
a=355
b=113
f <- function(k){
dk=abs(floor(k*pi)/k-pi)
dk1=abs(floor(k*pi+1)/k-pi)
min(dk,dk1)
}
d=abs(a/b-pi)
k=1
while(f(k)>=d){
if(f(k)<d) break
k=k+1
}
k
> k
[1] 16604
虱潰しと違って瞬時に答がでました。
問題読み間違えた orz
http://codepad.org/GHLm2A9a main = do
print $ head [(d,x,y) | d<-[1..], let y = fromInteger d, let x = fromInteger $ floor $ y*pi, x/y > 2*pi -355/113]
print $ head [(d,x,y) | d<-[1..], let y = fromInteger d, let x = fromInteger $ ceiling $ y*pi, x/y < 355/113]
(16604,52163.0,16604.0)
(33215,104348.0,33215.0)
>>242 [kπ-1]/k は 考えなくていい?
二項係数 nCr を C[n,r] で表すとき、
Σ[k=0 to 2n] C[2(n-k),n-k]*C[2k,k] = 4^n を証明せよ。
f(x)=1/√(1-x)を二項展開してf(x)^2=1/(1-x)の係数比較。
>>248 Lv.1:計算で証明
Lv.2:組合せの考え方で証明
>>247 kπ に一番近い整数を求めたい訳ですが、数直線上に kπ を印し、そこから左に進んで
最初に見つかる整数か、そこから、右に進んで最初に見つかる整数 のどちらかです。
ガウス記号を使うと、前者は、[kπ]で表せるし、後者は、[kπ+1]です。
切り捨て関数といえるガウス記号を使う限りでは、[kπ-1]は考慮する必要がありません。
もし、ガウス記号ではなく、四捨五入関数を使うのであれば、それに放り込んだものが、最も近い整数だし、
切り上げ関数Ceil()を使うのであれば、Ceil(kπ)か、Ceil(kπ-1)のどちらかということになります。
>>243 アイデアを拝借して、プログラムを組んでみました。
分数の目標となる範囲をあらかじめ設定し、仮に設定した分数の値が大きすぎれば、分母を大きくし、
小さすぎれば、分子を大きくし、...を繰り返し、範囲に収まる分数を探すという方法です。
http://codepad.org/JrigZqIn 242の方法は、分母 n までチェックする場合、2n の候補を調べていましたが、
この方法は、あと、もう一工夫入れることで、(3/2)n 位の候補のチェックで済みそうで、
よりよいアルゴリズムだと思います。
>>251 初歩的な質問にご丁寧に解説いただいてありがとうございました。
>>251 虱潰し解の過程でに少数表示から分数表示に変換するスクリプトを書いてみた。
LU2fra <- function(L,U){
f <- function(n){
m=0
x=m/n
while(x<U){
if(L<x) return(m-1)
x=m/n
m=m+1
}
return(NULL)
}
n=1
while(is.null(f(n))){
if( !is.null(f(n)) ) break
n=n+1
}
cat(f(n),'/',n,'\n')
f(n)/n
}
dec2fra <- function(digit,precision=1e-3){
L=digit*(1-precision)
U=digit*(1+precision)
LU2fra(L,U)
}
走らせてみた。
> dec2fra(0.3333)
1 / 3
[1] 0.333333333
> dec2fra(0.1538)
2 / 13
[1] 0.153846154
> dec2fra(0.2040)
10 / 49
[1] 0.204081633
> dec2fra(pi,1e-5)
355 / 113
[1] 3.14159292
そこそこ使える。
等面四面体の切断面の面積をできる限り手間なく求める方法はないでしょうか。
直方体に埋め込んでもかなりの計算量で困っています。
>>256 埋め込んで座標設定しても計算が面倒というなら統一的なうまい方法はないんじゃね
>>256 三点の座標を入力したら三角形の面積を計算するプログラム組めばいんじゃない?
Rで書くとこんな感じ
area3 <- function(A,B,C){
a=sqrt(sum((B-C)^2))
b=sqrt(sum((C-A)^2))
c=sqrt(sum((A-B)^2))
s=(a+b+c)/2
return(sqrt(s*(s-a)*(s-b)*(s-c)))
}
2以上の自然数nに対して、
1+2^(1/2)+3^(1/3)+...+n^(1/n)
は無理数であることを証明せよ
>>262 チェビシェフの定理からn/2 より大きく、n以外である素数pがとれる。
KをQにi^(1/i)(1 ≦i≦ n 、i ≠p)を添加して得られる体のガロア閉包、MをQにp^(1/p)を加えたガロア閉包、L=KMとするとGal(K/Q)の位数はpを割らないのでp^(1/p)はKにはふくまれない。
ここで tr[L/M](2^(1/2)+‥n^(1/n) はp^(1/p)[L:K] であるから主張は示された。
>>216 >>218 >>225 Wolfram先生に訊きました。
K(a) = { (x,y,z) | (xx+1)(yy+1)(zz+1)≦a},
V(a) = 8∫[0,√(a-1)]∫[0,√(a-1)] √{[ a/(xx+1)(yy+1) - 1]/2 + | a/(xx+1)(yy+1) - 1 |/2} dx dy,
V(125) = 479.663
V(8) = 33.657
辺々引いて
V(125) - V(8) = 446.006
>>262 最小多項式は
P_1(x) = x -1,
P_2(x) = x^2 -2x -1,
P_3(x) = x^6 -6x^5 +9x^4 -2x^3 +9x^2 -60x +50,
P_n(x) = P(x-a) P(x-aω) P(x-aω^2) …… P(x-aω^{n-1}),
ただし P(x) = P_{n-1}(x), a=n^(1/n), ω = exp(2πi/n).
空間の原点をO、点(10,0,0)をAとする。
Oからの距離が1以上2以下の点全体からなる領域をD、aを正の数としてAからの距離がa以上(a+1)以下の点全体からなる領域をD_aとおく。
DとD_aとの共通部分の体積が最大となるとき、[a]を求めよ。
ただし[x]でxを超えない最大の整数を表す。
共通部分はxy平面で切った図形の回転体だから、7≦a≦9と10≦a≦12の場合の面積(それぞれa=8,a=11で最大)を比較すればいいが
ちょっとめんどくさい
>>266 たとえばn=4のとき4^(1/4)=2^(1/2)になるから、それ一般にQ上規約にならんでしょ?
>>267 (1,2)と(a,a+1)が一致するときじゃないのか?
>>267 O (0,0,0)
A (L,0,0)
Aからの距離がa以下、Oからの距離がb以下 である点全体からなる領域の体積をV(a,b) とする。
・a+b ≦ L のとき V(a,b) = 0
・|a-b| ≧ L のとき V(a,b) = (4π/3)・min{a,b}^3
・|a-b| ≦ L ≦ a+b (△条件)のとき
2球面の交差円を含む平面を x=c とすると
c = (LL-aa+bb)/2L,
L-c = (LL+aa-bb)/2L,
V(a,b) = (π/3)(2a+L-c)(a-L+c)^2 + (π/3)(2b+c)(b-c)^2
= (π/12L)(a+b-L)^2 {(a+b+L)^2 -4aa +4ab -4bb)}.
>>267 DとD_aとの共通部分の体積は V(a+1,2) - V(a,2) - V(a+1,1) + V(a,1)
質問スレの問題
http://2chb.net/r/math/1534342085/374 くじ引きと料金に関する質問です
1)30%で当たる1回300円のくじ引き
2)60%で当たる1回800円のくじ引き
くじ引きは毎回戻して同じ確率で引く
当たりは一度だけ引けば良い場合
どちらの方が安く当たりを引く確率が高いですか?
を少し変えてみた。
くじ引きと料金に関する質問です
1)100本中30本当たりの1回1000円のくじ引き
2) 50本中30本当たりの1回2000円のくじ引き
くじ引きは戻さないで次のくじを引く
どちらの方が安く当たりを引く確率が高いですか?
4チームで総当たり戦を行う。引き分けは無いとすると、
(1) 結果は何通りあるか?
(2) そのうち上位2チームが決まらないものは何通りあるか?
(3)
アジア大会の野球競技ではSuper Roundが行われており、日本はあと1勝でもすれば決勝進出、2戦とも負けても台湾が全勝かつ中国が韓国に勝てば同率2位である。
現時点での各チームの勝敗はどうなっているか?
ごめん、(3)訂正
アジア大会の野球競技ではSuper Roundが行われており、日本は次の試合を勝てば決勝進出、負けても台湾が全勝かつ中国が韓国に勝てば同率2位である。
現時点での各チームの勝敗はどうなっているか?
試合が終わったので解答
(1)
「勝数の合計は必ず6になる」という必要条件を考慮して数え上げると
勝-敗
A:3-0, B:2-1, C:1-2, D:0-3 24通り
A:3-0, B:1-2, C:1-2, D:1-2 4通り ★
A:2-1, B:2-1, C:2-1, D:0-3 4通り ★
A:2-1, B:2-1, C:1-2, D:1-2 6通り
計38通り
(2)
★をつけた8通り
(3)
日○-●中
台○-●韓
韓○-●日
なお、さっき台湾vs中国の試合が終わり
台○-●中
>>271 >>272
V(a,2) - V(a,1)
= 0 (a≦L-2)
= (π/12L)(a+2-L)^2 {(a+2+L)^2 -4(aa -2a -4)} (L-2≦a≦L-1)
= (π/12L)(a+2-L)^2 {(a+2+L)^2 -4(aa -2a -4)}
- (π/12L)(a+1-L)^2 {(a+1+L)^2 -4(aa -a +1)} (L-1≦a≦L+1)
= (π/12L)(a+2-L)^2 {(a+2+L)^2 -4(aa -2a -4)} - (4π/3) (L+1≦a≦L+2)
= 0 (L+2≦a)
a = 10.1267741 のとき
V(a+1,2) - V(a+1,1) - V(a,2) + V(a,1) = 9.9571649074689 (最大)
V(a+1,2) - V(a+1,1) = 24.6422247200042
V(a,2) - V(a,1) = 14.6850598125353
V(a+1,2) = 28.8310149247906
V(a+1,1) = 4.1887902047864 = 4π/3,
V(a,2) = 17.0995582899984
V(a,1) = 2.4144984774631
>>267
[a] = 10 >>276 4チームの勝数で区別したとき、
3210 24通り
3111 8通り
2220 8通り
2211 24通り の合計64通りとカウントすべき
合計6試合あり、それぞれ二通りのパターンがあるから、2^6で64通り。38通りな訳がない。
3111or2220の8通りは、どのチームが全勝or全敗するかで4通り、
残り三チームの三すくみが右回りか左回りかで2通りあり、合計8通り
2211の24通りは、3210型の結果において、1位のチームと4位のチームの対戦の結果が
ひっくり返った場合に相当するので、3210型と同じ24通りになります。
△ABCの各頂点から対辺に下ろした垂線の足をS,T,Uとする。
AS+BT+CU=AS・BT・CUとなる三角形の形状を決定せよ。
>>280 なんか問題変じゃね?
外接円の半径をRとして
AS = 2R sin B sin C、
BT = 2R sin C sin A、
CU = 2R sin A sin B
だから
与式 ⇔ (sin B sin C + sin C sin A + sin A sin B)/(sin A sin B sin C)^2 = 4R^2
A,B,Cに何入れても与式を成立せしめる R が存在して形状なんか決定できない希ガス。
>>260 4点の座標を入力したらそれらを結ぶ四面体の体積を求めるRのスクリプトを書いてみた。
但し、高さの算出は近似計算
改造歓迎
library(nleqslv)
Tetra <- function(O=c(1/2,sqrt(3)/6,sqrt(2/3)),A=c(0,0,0),B=c(1,0,0),C=c(cos(pi/3),sin(pi/3),0)){
fn <- function(x,O,A,B,C){
AO=A-O
BO=B-O
CO=C-O
HO=x[1]*AO+x[2]*BO+(1-x[1]-x[2])*CO # H on triangle ABC
AB=B-A
AC=C-A
c(HO%*%AB,HO%*%AC) # HO vertial to AB and AC
}
fn1 <- function(x) fn(x,O,A,B,C)
x=nleqslv::nleqslv(c(1/3,1/3),fn1)$'x'
AO=A-O
BO=B-O
CO=C-O
HO=x[1]*AO+x[2]*BO+(1-x[1]-x[2])*CO
h=sqrt(sum(HO^2))
a=sqrt(sum((B-C)^2))
b=sqrt(sum((C-A)^2))
c=sqrt(sum((A-B)^2))
s=(a+b+c)/2
base=sqrt(s*(s-a)*(s-b)*(s-c))
V=1/3*base*h
return(V)
}
>>280 AS=1、BT=x、CU=yとおくと、題意より、
1+x+y=xy
y=(x+1)/(x-1)
∥∩∩∥∩∩ ∥∴
( (`)(^o^))∥x>1
(っ[ ̄]っц)∥y>1
「 ̄ ̄ ̄ ̄ ̄]∥即ち
□/_UU__UU□∥ △ABCは鈍角三角形 次の条件を満たす関数f(x)が存在すればそれを求め
存在しなければそれを証明せよ
(1) 実数全体で微分可能
(2) x≠0 なる任意の実数 x に対して x^2 f’(x)=f(x)
(3) f(1)=1
>>284 f '(x)/f(x) = 1/xx,
log f(x) = c - 1/x,
f(x) = e^(c -1/x),
f(1)=1 より c=1
f(x) = e^(1 -1/x)
x=0 で微分可能ではないだろうな。
>>282 4点の座標が判っているなら、ベクトルの三重積(の絶対値の1/6)で体積求まりますよ。
つまり、一つの点が原点になる様に平行移動して、残り三点を
(x1,y1,z1),(x2,y2,z2),(x3,y3,z3) としたら、
V=(1/6) | x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1 |
>>287 ありがとう御座います。スクリプトの検証に使わせていただきます。
>>287 ご教示の通りにスクリプトを書いたら僅か4行で済みました。
ありがとうございました。
tetrahedron <- function(O=c(1/2,sqrt(3)/6,sqrt(2/3)),A=c(0,0,0),B=c(1,0,0),C=c(cos(pi/3),sin(pi/3),0)){
AO=A-O
BO=B-O
CO=C-O
as.numeric(abs(pracma::cross(AO,BO) %*% CO)/6)
}
どれも一致しました。
> sqrt(2)/12
[1] 0.1178511301977579
> Tetra()
[1] 0.1178511301977579
> tetrahedron()
[1] 0.1178511301977579
前
>>283 AS=1
BT=x>1
CU=y>x>1
とすると、
1+x+y=xy
y=(x+1)/(x-1)
=1+2/(x-1)>1
y-x=(x+1)/(x-1)-x
={(x+1)-x(x-1)}/(x-1)
=(1+2x-x^2)/(x-1)>0
1+2x-x^2>0
1<x<1+√2
x=1.1のときy=21
x=2.4のときy=17/7=2.42857……>1+√2
1<x<1+√2<y
三つの垂線の大小を、
AS<BT<CUとすると、
AS<BT<AS+√2<CU
前
>>290 AS=1
BT=x>1
CU=y>x>1
とすると、
1+x+y=xy
y=(x+1)/(x-1)
=1+2/(x-1)>1
y-x=(x+1)/(x-1)-x
={(x+1)-x(x-1)}/(x-1)
=(1+2x-x^2)/(x-1)>0
1+2x-x^2>0
1<x<1+√2
x=1.1のときy=21
x=2.4のときy=17/7=2.42857……>1+√2
1<x<1+√2<y
直角三角形の相似かな。
鋭角三角形でも可能なような。
>>284 f(x)の値を
e^(1-1/x) (x>0 の時)
0 (x≦0 の時)
と定めればこのfは条件を満たす。
>>292 まったりと地雷踏んでくれてありがとう。
そう定義すると
x=0 に対しても x^2 f ’(x) = f(x)
が成り立ってしまうから。
>>293 成り立っていると、どうししてダメなの?
高校数学でつ。
nは自然数とする。1から5nまでの数字がそれぞれ書かれた5n枚のカードから2枚選んでその数字をx、yとする。
x^2+y^2
の一の位が7となる確率をPnとするとき、極限値
lim(n→∞)(25Pn/2)⁵ⁿ
を求めよ。
>>299 xx+yy の一の位が 7
⇔ xx, yy の一の位が {1,6} または {6,1}
⇔ x, yの一の位が {1または9, 4または6} または {4または6, 1または9}
5n枚のカードのうち、一の位が 1または9 のものは n枚。
一の位が 4または6 のものは n枚。
Pn = 2/25.
1.
>>296 >>284 (2) は x=0 に対しては … が成り立たないことを示唆する。
>>284 (2) が
任意の実数 x に対して x^2 f ’(x)=f(x)
だっから
>>292 で正解だが…
>>301 >
>>284 (2) は x=0 に対しては … が成り立たないことを示唆する。
バカバカしい。
>>301 君、命題の裏が恒真だと思ってる?
高校数学からやり直した方がいいよ
>>299 カードは戻すの?戻さないの?
あと極限の式を正確に書け
ただの宿題なら質問スレへ
>>299 1枚目のカードを戻さない場合は
Pn = 2nn/{5n(5n-1)},
(25/2)Pn = 1/(1 - 1/5n)
lim(n→∞) {(25/2)Pn}^(-5n) = lim(n→∞) (1 - 1/5n)^(5n) = 1/e,
lim(n→∞) {(25/2)Pn}^(5n) = e,
f'(x)が全実数で定義できるが0で連続じゃないって相当性質悪い関数しかなさそうだが
x=0 でも成立つのに、わざわざ「x≠0 なる任意の実数xに対して」と言うところがキモ。
緩めても他の解が出てくるわけぢゃないし。
>>301 例えば、(リーマン)積分では有界閉区間上の連続関数f:[a,b]→Rを扱うけど、このときfは[a,b]以外では定義されてたら(もしくは連続だと)駄目なんですね?
群準同型f:G→Hの定義にf(e)=eという条件があるけど、これはg∈Gについて「g=eならばf(g)=e」という条件だから、g≠eのときf(g)=eとなったら駄目なんですね?
つまりker(f)={e}となって、群準同型は常に単射になるんですね?
……アホか
>>305 指摘ありがとう
二枚のカードは同時に取り出します
自作問題なんです気を付けます、、、
>>306 正解です
>>301 x≠0で云々、というのは、x=0のときについては何も言ってないよね?
確かに一般的な感覚とはずれてますが
>>308 同じ結果我得られるなら仮定はできるだけ緩くするのは当然だろ
何いってんの
>>308 緩めて他の解がでてこないなら益々あかんやろ。
出てくるなら ”それは解を尽くせてないからダメ” といえなくはないけど。
(正解)
① … 2*{(2n-1)*(2n)/2} = 4n^2-2n 試合
② … 2*{n^2} = 2n^2 試合
③ … 2 試合
総試合数は 6n^2-2n+2 試合
(別解1)
A組上位とB組下位、B組上位とA組下位の間の試合( 2n^2 試合)が省略、三決と決勝が追加されると考えて、
8n^2-2n-2n^2+2 = 6n^2-2n+2 試合
(別解2)
①と②で各チーム必ず (2n-1)+n = 3n-1 回戦うから (3n-1)*4n/2 = 6n^2-2n 試合
③の2試合を足して 6n^2-2n+2 試合
今年の大会だと
U12アジア選手権 4n = 8 22 試合
U-15野球W杯 4n = 12 50 試合
U18アジア選手権 4n = 8 22 試合(予定)
U-23野球W杯 4n = ? ?? 試合(未定)
アジア競技大会 野球 4n = 8 22 試合(ただし3チームが最後の1枠を争う予選が3試合あった)
女子野球W杯 4n = 12 50 試合
10人を空部屋なしで5部屋を割り当てる、但し、各部屋の定員は3人とする。割り当て方は何通りあるか。
(10!/(2!2!2!2!2!)/5! + 10!/(3!2!2!2!1!)/3! + 10!/(3!3!2!1!1!)/2!/2! ) * C[10,5]
まちがえた
(10!/(2!2!2!2!2!)/5! + 10!/(3!2!2!2!1!)/3! + 10!/(3!3!2!1!1!)/2!/2! ) * P[10,5]
(10!/(2!2!2!2!2!)) /5! = 945,
(10!/(3!2!2!2!1!)) /3! = 12600,
(10!/(3!3!2!1!1!)) /(2!2!) = 12600,
945 + 12600 + 12600 = 26145,
26145 * 5! = 3137400,
>>316 各部屋に一人ずつ5人入れると、その入れ方は5!=120通り。
あとから入る5人の入れ方は、
1、1、1、1、1が1通り
2、1、1、1、0が5×4=20通り
2、2、1、0、0が5×(4C2)=5×4!/2!=30通り
だが、だれがどの部屋に入るか公平に決めないといけないから、
1、1、1、1、1が5!=120通り
2、1、1、1、0が20×(5C2)×3!=1200通り
2、2、1、0、0が30×5×(4C2)=900通り
合計2220通り
先に入るかあとから入るかは確率1/2だから二倍すると、
(120+2220)×2=4680通り
先に入るかあとから入るかで公平さは変わらない。
前
>>320 結果的にその部屋に決まるなら、先に入ろうがあとから入ろうが同じ。
2340通り
まず初めに最初に部屋に入る人を選ばないといけないから、
(10C5)×2340
=10×9×8×7×6×2340
=70761600
前>>321
部屋に名前をつけて検証する。部屋を(北西)(北)(西)(中央)(東南の角部屋)の五つとする。
人に①~⑩の番号を振る。(北西)(北)
┏━━┳━━┓
┃① ┃② ┃
┃ ┃⑥④┃
┣━━╋━━╋━━┓
┃③ ┃⑤⑨┃⑦⑩┃
┃ ┃⑧ ┃ ┃
┗━━┻━━┻━━┛
(西)(中央)(東南の角部屋)
試しに①~⑩の被験者に順に部屋に入ってもらった。このとき、①~⑥まではどこでも入れたんですんなり入ってくれたが、⑦が困った。一部屋いっぱいで。つまり(北)が。つまり4択という不公平感。⑩にいたっては3択だった。
5^6×4^3×3=300万通り
一回の施行で少なくともこれだけある。何千通りじゃ足りない。 前
>>325 一回の施行というか試行で300万通りという値を得たが、少なくとも300万通りあるんであって、実際はもう少し変わった部屋割りが可能だから増えると感じた。つまり二人部屋を多くしたりとかほかのパターンがある。
>>319この値は信憑性がある。
>>134>>135
解答です。
ネットで見つけた素晴らしいNoteに依ります。
---- 解答例 ----
以下では初期配置における玉の総数が偶数である場合を考える。
奇数の場合はE(X[2n])とE(X[2n-1])の結論が逆となるだけである。
自然数 j で玉が j 個ある状態を表すとする。系を HMC([1]、p3) と考える。
まず不変分布 π[n] ([1]、p11)を求める。
π[n] = aπ[n-1]/(n-1+0) + (n+1-a)π[n+1]/(n+1+0)
である。ただしp/(q+0) = lim[ε→0]p/(q+ε)である。
f(x) = Σπ[n]x^n、g(x) = Σπ[n]/(n+0)x^nとおけば
(x-1)g′(x)=a x-x g(x)
となり、これを解いてg(x) = Ax^ae^(ax) を得る。よって
f(x) = xg′(x) = Aa(x + 1)x^ae^(ax) である。
ここで f(1) = 1 により
f(x) = (x+1)x^ae^(ax) / (2e^a)
を得る。以上によりこの HMC は π[n] = f (1) < ∞ を満たす不変分布を持つから、正再帰的 HMC ([1]、p13)である。
また p_{aa}^(2) > 0、奇数 n に対して p_{aa}^(n) = 0 で あるから周期は 2 である。([1]、p5)
以上により初期の玉の総数が偶数であることから
lim[n→∞]E(X[2n])
= f′(1) + f′(-1)
= 1 {e^a +2a+2a+(-1)^ae^(-a)}/(2e^a)
= 2a + 1/2 + (-1)^a/(2e^a)
lim[n→∞]E(X[2n-1])
= f′(1) - f′(-1)
= 1 {e^a +2a+2a-(-1)^ae^(-a)}/(2e^a)
= 2a + 1/2 - (-1)^a/(2e^a)
である。([1]、p19)
ref.
[1] マルコフ連鎖、
https://www.komazawa-u.ac.jp/~toshi/teaching/TIT/note1.pdf
[2] a=10、玉の総数が100の場合、
>>182、
----
どうも東大の講師の方の講義のレジュメのようです。
収束証明とか感動的です。
カップリングとか言われたらわかるけど、こんなん絶対思いつかん。
しまった。リンクまちがった。
赤10、白90のより精密な数値シュミレーション例
>>181。
1001 : 0000020.50000000103057681723857863179375573
1002 : 0000020.49999999896942319451989818931917708
1003 : 0000020.50000000103057681669136956653754163
1004 : 0000020.49999999896942319399815481629102060
1005 : 0000020.50000000103057681619390677994098141
1006 : 0000020.49999999896942319352384265899269428
1007 : 0000020.50000000103057681574166788303501812
1008 : 0000020.49999999896942319309264978872148864
1009 : 0000020.50000000103057681533054161312050221
1010 : 0000020.49999999896942319270065627029311700
ちなみに
1/(2e^10) = 1.030576811219279e-9
>>330 さらに訂正。
lim[n→∞]E(X[2n])
= f′(1) + f′(-1)
= {e^a +2ae^a+2ae^a+(-1)^ae^(-a)}/(2e^a)
= 2a + 1/2 + (-1)^a/(2e^a)
lim[n→∞]E(X[2n-1])
= f′(1) - f′(-1)
= {e^a +2ae^a+2ae^a-(-1)^ae^(-a)}/(2e^a)
= 2a + 1/2 - (-1)^a/(2e^a)
まだあるかもだけどエスパーしてちょ。
(北西)(北) 前>>329
┏━━┳━━┓部屋割り
┃①②┃④⑤┃ だな。
┃③ ┃⑥ ┃
┣━━╋━━╋━━┓
┃⑦⑧┃⑨ ┃⑩ ┃
┃ ┃ ┃ ┃
┗━━┻━━┻━━┛
(西)(中央)(東南の角部屋)
「奥から詰めてください」学級委員の指示で北西と北が三人部屋になった。「空き部屋を作らないように」
⑦と⑧は仲良しだから喜んだ。
⑦「どの部屋を選ぶか最初の奴らは5通りだが、俺ら入るときは三人部屋ができてて3通りしかないだろ」
⑧「不公平だな。部屋の決め方がまず5!通りある。あとは5部屋をそれぞれ何人ずつにするか」
⑦「今回は3、3、2、1、1だ」
⑧「ほかに3、2、2、2、1と2、2、2、2、2があるな」紙に書きながら言う。
⑨「俺が計算してやろうか」襖をあけた⑨が言った。
⑦「入ってくるなよ」これを拒んだ。
⑨「おお」うなずいて、「人数変わってデータが狂うからな」手をのばし、⑧から紙を受けとると、なにか書いた。
『(10!/3!・3!・2!・1!・1!・2!・2!
+10!/3!・2!・2!・2!・1!・3!
+10!/2!・2!・2!・2!・2!・5!)×5!
={(10×9×8×7×6×5)/(3×2×2)+(10×9×8×7×6×5)/(2×3×2)+(10×9×8×7×6×5×4×3)/(2×2×2×2×5!)}×5!
={(5040/4)×2+(5040×90)/(2×2×5!)}×5!
={2520+(2520×9)/24}×5!
={2520+(2520×3)/8}×5!
=2520×(11/8)×5!
=2520×11×5×3
=12600×33
=330000+66000+18000+1800
=396000+19800
=415200
あれ、計算間違いかな?
(シッピン)(グニ)
41も52も吉数なんだが。 Prelude> let fact x = product [1..x]
Prelude> (* (fact 5)) $ sum [div (fact 10) (product $ map fact a) | a<-[[2,2,2,2,2,5],[3,2,2,2,1,3],[3,3,2,1,1,2,2]]]
3137400
前
>>333計算間違いだ。
『(10!/3!・3!・2!・1!・1!・2!・2!
+10!/3!・2!・2!・2!・1!・3!
+10!/2!・2!・2!・2!・2!・5!)×5!
={(10×9×8×7×6×5)/(3×2×2)+(10×9×8×7×6×5)/(2×3×2)+(10×9×8×7×6×5×4×3)/(2×2×2×2×5!)}×5!
={(10×9×4×7×5)×2+(10×9×7×3)/2}×5! ={25200+945)×5!
=26145×5×4×3×2
=26145×120
=2614500+522900
=3137400(通り)
コンピュータに数えさせました。
library(gtools)
n=5
r=10
c=3
perm=permutations(n,r,rep=T)
tail(perm)
g <- function(x) all(1:n %in% x)
system.time(g(perm[1:1e6,])) # fast
i=which(apply(perm,1,g)) # lengthy
perm5=perm[i,]
tail(perm5)
j=length(i)/factorial(5)
h <- function(x) max(table(x)) <= c
k=which(apply(perm5[1:j,],1,h))
length(k)
length(k)*factorial(5)
l=which(apply(perm5,1,h)) # lengthy
length(l)
答は>319の通り
> length(l)
[1] 3137400
>>336 最初と最後を書くとこんな感じ
> head(perm53) ;tail(perm53)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 1 2 2 2 3 3 4 5
[2,] 1 1 1 2 2 2 3 3 5 4
[3,] 1 1 1 2 2 2 3 4 3 5
[4,] 1 1 1 2 2 2 3 4 4 5
[5,] 1 1 1 2 2 2 3 4 5 3
[6,] 1 1 1 2 2 2 3 4 5 4
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[3137395,] 5 5 5 4 4 4 3 2 1 2
[3137396,] 5 5 5 4 4 4 3 2 1 3
[3137397,] 5 5 5 4 4 4 3 2 2 1
[3137398,] 5 5 5 4 4 4 3 2 3 1
[3137399,] 5 5 5 4 4 4 3 3 1 2
[3137400,] 5 5 5 4 4 4 3 3 2 1
10人を5部屋に割り当てるときに空室があってもよいが1部屋の定員は3とすると 4229400通り数えられた。
library(gtools)
n=5
r=10
c=3
perm=permutations(n,r,rep=T)
tail(perm)
h <- function(x) max(tabulate(x))<=c
idx3=which(apply(perm,1,h))
perm3=perm[idx3,]
tail(perm3) # 定員3空室可
> tail(perm3)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[4229398,] 5 5 5 4 4 4 3 3 2 3
[4229399,] 5 5 5 4 4 4 3 3 3 1
[4229400,] 5 5 5 4 4 4 3 3 3 2
>
g <- function(x) all(1:n %in% x)
system.time(apply(perm3[1:1e5,],1,g)) # fast
idx35=which(apply(perm3,1,g))
perm35=perm3[idx35,]
tail(perm35) # 定員3空室不可
> tail(perm35)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[3137398,] 5 5 5 4 4 4 3 2 3 1
[3137399,] 5 5 5 4 4 4 3 3 1 2
[3137400,] 5 5 5 4 4 4 3 3 2 1
g <- function(x) all(1:n %in% x) #
system.time(apply(perm[1:1e5,],1,g)) # fast
i=which(apply(perm,1,g)) # lengthy
perm5=perm[i,] #定員なし空室不可
> tail(perm5)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[5102998,] 5 5 5 5 5 5 4 2 3 1
[5102999,] 5 5 5 5 5 5 4 3 1 2
[5103000,] 5 5 5 5 5 5 4 3 2 1
今回はこれぐらいにしといてやる。前>>335口ほどにもない易問やったなぁ。
((-.-)
(っц)~
「 ̄ ̄ ̄]台風も最大いうほどたいしたことないし。もうそろそろ日本海か。
○田くん、さびしなったはんのかな。知り合いも知り合いやよな。敵に言わんといて言うたはんのにや。頼れるもんなくなっていくんはきついやろで。でも記録は記録なんやろ。逃走の。 ニュー速+でみつけた問題
男が90人女は10人、医学部を受験しました。学力は同程度だと仮定します。合格できるのは10人です。
では女の合格率が男と同程度以上になる確率はいくらでしょう?
女子が1人以上合格すると(女子の合格率)≧(男子の合格率)となる
女子が1人も合格しない確率は(1/2)^10=1/1024
求める確率は1-1/1024=1023/1024
>>341 man=90
woman=10
pass=10
total=man+woman
p=pass/total
i=0:10
#
女子>男子
> sum((choose(woman,i)*choose(man,pass-i)/choose(total,pass))*(i/woman > (pass-i)/man))
[1] 0.2615285
女子=男子
> sum((choose(woman,i)*choose(man,pass-i)/choose(total,pass))*(i/woman == (pass-i)/man))
[1] 0.4079953
女子<男子
> sum((choose(man,i)*choose(woman,pass-i)/choose(total,pass))*(i/man > (pass-i)/woman))
[1] 0.3304762
______」|
( -~-) |
_'``'____」
 ̄ ̄ ̄ ̄ ̄ ̄ ̄今宵は嵐じゃ。あしたは暑くなる。寝るぞ。前>>341すでに同程度言うたはるやろ。同程度以上になる確率は1/2(二分の一)や。不正はあかん。公平やないと。それが試験ちゅうもんや。 男子900人受験、女子100人受験、定員100人のときはこうなった。
> sum((choose(woman,i)*choose(man,pass-i)/choose(total,pass))*(i/woman > (pass-i)/man))
[1] 0.4160339
> sum((choose(woman,i)*choose(man,pass-i)/choose(total,pass))*(i/woman == (pass-i)/man))
[1] 0.1389853
> sum((choose(man,i)*choose(woman,pass-i)/choose(total,pass))*(i/man > (pass-i)/woman))
[1] 0.4449808
>>344 コインを4回投げて表が必ず2回でなくちゃ不正なのか?
3回だったらどうすんの?
>>346 コインを3回投げたら1回表、1回裏、残りはコインが立たなくちゃ不正なのか?
>>341 興味が湧いたので
定員10人受験生100人でそのうち女子の数が変化したときに
男女の合格率のどちらが高くなるかの確率をグラフにしてみた。

______」|
(-゚- ) |
_'``'____」
 ̄ ̄ ̄ ̄ ̄ ̄ ̄アンカー間違えた。前々>>344前>>340合格率が同じってことは男10人女1人だ。同程度以上になる確率が1/2、同程度未満になる確率が1/2、あわせて1。これが公平ってことだ。
が実際には片寄りが出る。なぜなら男女別で審査してないから。同じ問題を同じ条件で解くと同程度になるはずだが実際はやってみないとわからない。
ただ男から10人、女から1人を選ぶような条件付きの試験じゃないってことだ。男が11人受かることもあれば、女が2人受かることもある。 前
>>349違うな。訂正。
男が10人受かることもあれば、女が2人受かることもある。
以前は、このスレだけは多少なりとも参加する価値があったんだがな。
この惨状。
数学板だから、空気が読めなくても数学ができれば別にいいんだが
空気が読めなくてバカでコテハンでイキリ厨房っていうね…
>>344 たまーに まともなことも言う。
製造業、建設業、商業… 世に職業はいろいろあるが、大学の売り物は公正さぐらいしかない。
それを損なっては、仕事のないトクニンの溜まり場でしかなくなる。
自分らの値打ちを自ら下げてどうする。
学生は、くれぐれもこういう真似をしないように。
では問題です。[前スレ
>>535]
〔問題100〕
a, b, c, d が正のとき
(a-b)(a-c)/(a+b+c)
+ (b-c)(b-d)/(b+c+d)
+ (c-d)(c-a)/(c+d+a)
+ (d-a)(d-b)/(d+a+b)
≧ 0,
を示せ。
IMO-2008 Short list A.7
不等式bot(@inequalitybot) [100] ☆12
まぁこの手の問題はアルゴリズムが発見されてるからなぁ。
>>354 [前スレ.961]
煩雑で汚い解答の例
(1) まづ a-c, b-d の斉2次式で表わす。
2 (左辺) = F (a-c)^2 + H (a-c)(b-d) + G (b-d)^2,
ここに
F = 1/(c+d+a) + 1/(a+b+c),
G = 1/(b+c+d) + 1/(d+a+b),
H = 3{ -(a+c)/(c+d+a)(a+b+c) + (b+d)/(d+a+b)(b+c+d)},
とおいた。この斉2次式が正定値となる条件は、
(判別式) = HH - 4FG < 0,
(2) F, G, H を評価する。
相加-調和平均で
F = 1/(c+d+a) + 1/(a+b+c) ≧ 4/{2(a+c)+(b+d)},
G = 1/(b+c+d) + 1/(d+a+b) ≧ 4/{(a+c)+2(b+d)},
∴ FG ≧ 16/{2(a+c)^2+5(a+c)(b+d)+2(b+d)^2} ≧ 16/{(9/4)(a+b+c+d)^2} > 7/(a+b+c+d)^2,
0 < (a+c)/(c+d+a)(a+b+c) = (a+c)/{(a+c)(a+b+c+d)+bd} < 1/(a+b+c+d)、
0 < (b+d)/(b+c+d)(c+d+a) = (b+d)/{(b+d)(a+b+c+d)+ac} < 1/(a+b+c+d)、
∴|H| < 3/(a+b+c+d)、
よって (判別式) = HH - 4FG < 0,
∴ 左辺は正定値。
じゃあ関連して
(問題)
有理係数の多項式 P(x1,…,xn) が与えられた時、∀x1…xn P(x1,…,xn) ≧ 0 ならその証明を、そうでないならその反例を与えるアルゴリズムが存在することを示せ。
>>345 これをグラフ化した。

男子90n人、女子10n人、定員10n人 とする。
・女子>男子
Σ[n < k ≦10n] C[90n,10n-k] C[10n,k] / C[100n,10n]
・女子=男子
C[90n,9n] C[10n,n] / C[100n,10n]
・女子<男子
Σ[0≦ k < n] C[90n,10n-k] C[10n,k] / C[100n,10n]
n=1 のとき >>343
> 0.2615284665839845
= 0.4079953223292903
< 0.3304762110867252
n=10 のとき >>345
> 0.41603390750170235
= 0.13898526767704465
< 0.4449808248212530 >>360 n→∞ のとき正規分布に近づく(?)
> 1/2,
= (5/9)√(2/πn) = 0.4432692/√n,
< 1/2,
>>360 >>361 Stirling の近似式
log(m!) ≒ (m+1/2)log(m) -m +(1/2)log(2π) +1/(12m),
を使えば
log(C[10m,m]) ≒ b m - (1/2) log(m) + (1/2) log(5/9π) - c/12m,
ここに
b = 10 log(10) - 9 log(9) = 3.250829734
c = 1 + 1/9 -1/10 = 91/90,
= となる確率は
(5/9)√(2/πn) exp(cc/12n),
= (0.443269200446/√n) exp(0.085195473251/n)
>>339 r人をn部屋に割り当てるときに(n=5, r=10) 各部屋の定員がc人だとする。
・定員c=3、空室可
(r!/(3!3!2!2!0!)) /(2!2!) = 6300,
(r!/(3!3!3!1!0!)) /3! = 2800,
を含めて
26145 + 6300 + 2800 = 35245,
35245 * n! = 4229400,
・定員なし、空室不可
(r!/(4!2!2!1!1!)) /(2!2!) = 9450,
(r!/(4!3!1!1!1!)) /3! = 4200,
(r!/(5!2!1!1!1!)) /3! = 2520,
(r!/(6!1!1!1!1!)) /4! = 210,
を含めて
26145 + 9450 + 4200 + 2520 + 210 = 42525,
42525 * n! = 5103000,
・定員なし、空室可
5^r = 9765625,
(内訳)
空室0 … C[n,0] (5^r - 5・4^r + 10・3^r - 10・2^r + 5・1^r) = 5103000,
空室1 … C[n,1] (4^r - 4・3^r + 6・2^r -4・1^r) = 4092600,
空室2 … C[n,2] (3^r - 3・2^r + 3・1^r) = 559800,
空室3 … C[n,3] (2^r - 2・1^r) = 10220,
空室4 … C[n,4] (1^r) = 5,
男子5人女子5人を空室なし男女混合なしで5部屋に割り当てる方法は何通りあるか?
>>365 (C[5,1]×(C[1,0]1^5 - C[1,1]0^5)×(C[4,0]4^5 - C[4,1]3^5 + C[4,2]2^5 + C[4,3]1^5 + C[4,4]0^5)
+C[5,2]×(C[2,0]2^5 - C[2,1]1^5 + C[2,2]0^5)×(C[3,0]3^5 - C[3,1]2^5 + C[3,2]1^5 + C[3,3]0^5))×2
>
>>365 (C[5,1]×(C[1,0]1^5 - C[1,1]0^5)×(C[4,0]4^5 - C[4,1]3^5 + C[4,2]2^5 - C[4,3]1^5 + C[4,4]0^5)
+C[5,2]×(C[2,0]2^5 - C[2,1]1^5 + C[2,2]0^5)×(C[3,0]3^5 - C[3,1]2^5 + C[3,2]1^5 - C[3,3]0^5))×2
>>367 お見事です。
コンピュータのカウントと合致。
> tail(perm5[m,])
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[92395,] 5 5 5 5 5 4 4 1 2 3
[92396,] 5 5 5 5 5 4 4 1 3 2
[92397,] 5 5 5 5 5 4 4 2 1 3
[92398,] 5 5 5 5 5 4 4 2 3 1
[92399,] 5 5 5 5 5 4 4 3 1 2
[92400,] 5 5 5 5 5 4 4 3 2 1
次はこんな問題かな。
男子5人女子5人を空室なし男女混合なしで定員3の5部屋に割り当てる方法は何通りあるか?
部屋分け
(1) 3 :男(3,2)、女(3,1,1)または(2,2,1)
(2) 1: 男(3,1,1)、女(3,2)
(3) 1: 男(2,2,1)、女(3,2)
3+1+1=5通りかな?
簡単すぎ?
↑
(1) 2 :男(3,2)、女(3,1,1)または(2,2,1)
(2) 1: 男(3,1,1)、女(3,2)
(3) 1: 男(2,2,1)、女(3,2)
2+1+1=4通りかな?
ほかのことをしていた。注意しませう
部屋を1~5と命名すると
定員3で男女混合にならない部屋割はこんな感じ
男1 男2 男3 男4 男5 女1 女2 女3 女4 女5
[1,] 1 1 1 2 2 3 3 3 4 5
[2,] 1 1 1 2 2 3 3 3 5 4
[3,] 1 1 1 2 2 3 3 4 3 5
[4,] 1 1 1 2 2 3 3 4 4 5
[5,] 1 1 1 2 2 3 3 4 5 3
[6,] 1 1 1 2 2 3 3 4 5 4
>>371 いみがわからねえ
[1,] 1 1 1 2 2 3 3 3 4 5 の意味は
男3人、男二人、
女三人、女二人
4部屋しか使っていないからXじゃないの
男(3,2)、女(3,1,1)または(2,2,1)
とは意味が違うね
収容人数がそれぞれa,b,c,d+p人の部屋A,B,C,Dに、ちょうど(a+b+c+d)人を割り振る。
そのような方法は何通りあるか。
ただしa,b,c,dは自然数、pは非負整数とする。
>>372 男1 男2 男3 男4 男5 女1 女2 女3 女4 女5
[1,] 1 1 1 2 2 3 3 3 4 5
は
男1男2男3は部屋1に
男4男5は部屋2に
女1女2女3は部屋3
女4 は部屋4
女5は部屋5
に割り当てるという意味。
4人部屋の空床が5部屋あるとする。
男5人女5人の入院予約を受けた。
空室ができてもよいが男女混合部屋は不可とするとき
部屋割の方法は何通りあるか。
これ男性部屋の個数と収容人数で場合分けして数えたけど
もっと効率の良い数え方ってあるでしょうか?
>>375 つまり
男(3,2)、女(3,1,1)というわけですね
r人をちょうどn部屋に(定員なしで)割り当てる方法は、
A[r,n] = n^r - C[n,1](n-1)^r + C[n,2](n-2)^r - … + (-1)^(n-1) C[n,n-1] 1^r
= Σ[k=0,n-1] (-1)^k C[n,k] (n-k)^r,
r=5 のとき
A[r,1] = 1^r = 1,
A[r,2] = 2^r -2 = 30,
A[r,3] = 3^r -3・2^r +3・1^r = 150,
A[r,4] = 4^r -4・3^r +6・2^r -4・1^r = 240,
>>365-368
r = 5,
部屋の数が (男1,女4) (男2,女3) (男3,女2) (男4,女1)
C[5,1] A[r,1] A[r,4] + C[5,2] A[r,2] A[r,3] + C[5,3] A[r,3] A[r,2] + C[5,4] A[r,4] A[r,1]
= 5・1・240 + 10・30・150 + 10・150・30 + 5・240・1
= 92400, 男子5人女子5人を5部屋割り当てる。
部屋に定員はなし、空室があってもよい。
割り当てた部屋を全て男女混合にする方法は何通りあるか。
男(5) 女(2,1,1,1) (5!/5!) (5!/(2!1!1!1!))/3! = 10,
男(2,1,1,1) 女(5) (5!/(2!1!1!1!))/3! (5!/5!) = 10,
男(4,1) 女(3,1,1) (5!/(4!1!)) (5!/(3!1!1!))/2! = 50,
男(3,1,1) 女(4,1) (5!/(3!1!1!))/2! (5!/(4!1!)) = 50,
男(4,1) 女(2,2,1) (5!/(4!1!)) (5!/(2!2!1!))/2! = 75,
男(2,2,1) 女(4,1) (5!/(2!2!1!))/2! (5!/(4!1!)) = 75,
男(3,2) 女(3,1,1) (5!/(3!2!)) (5!/(3!1!1!))/2! = 100,
男(3,1,1) 女(3,2) (5!/(3!1!1!))/2! (5!/(3!2!)) = 100,
男(3,2) 女(2,2,1) (5!/(3!2!)) (5!/(2!2!1!))/2! = 150,
男(2,2,1) 女(3,2) (5!/(2!2!1!))/2! (5!/(3!2!)) = 150,
定員c=3 のとき
(100+100+150+150) * 5! = 60000, >>368
定員c=4 のとき
(50+50+75+75 + 100+100+150+150) * 5! = 90000,
定員c≧5(なし)のとき
(10+10 + 5+50+75+75 + 100+100+150+150) * 5! = 92400, >>365 >>381 整理されてわかりやすい解答ありがとうございました。
有理数の集合は可算個の開集合の共通部として表せないことを証明せよ
・QはRで稠密だから
・各開集合はある区間を含み、したがって無理数を含むから
・共通部分がある区間を含んでしまうと無理数を含むことになるから
・共通部品が無理数を含まないとしたら、当然どんな区間も含むことはないから
Q=∩Ui (Ui : open) とすると任意のiについて Ui はQを含む開集合だからR。
>>384 ∩_(n=1,∞) (-1/n,1/n)={0}
の通り 開集合の共通部分は開区間を含むとは限らない
>>385 なぜ任意のiに対してUiはQを含む?
共通部分の定義間違えてないか?
>>387 Q = ∩ Ui ⊂ Ui やん。加算個もへったくれもないやん。
>>388 ごめん頭ぶっ壊れてた
でもQを含む開集合はRとは限らないよ
閉包はもちろんRだけど
例えばR\{√2}
とかね
>>391 >・共通部分がある区間を含んでしまうと無理数を含むことになるから
これってある区間を含むことを導いて矛盾させるってことじゃないの?
>>393 すまん、アホな勘違いをしてたわ
むしろRから点を取り除く方向で行った方がいいかな……
というかもしかしてカテゴリー定理使う?
>>394 その通り
ベールのカテゴリー定理をすこーしだけ工夫して使えば終わり
[0,1]の一様乱数をn個発生させて,小さい順にa(1), ..., a(n)とする。
同様にもう一度n個の乱数を作って小さい順にb(1), ..., b(n)とする。
a(1)とb(1), a(2)とb(2), ...と同じ順位同士でペアを作り大小を比較する。
この時aのほうが大きいペアの数は0個~n個のいずれかになるが,その確率分布は?
>>398 シミュレーションしての予想、Norm(n/2,√n/2)
>>398
a(k) > b(k) となる確率 1/2
a(k) < b(k) となる確率 1/2
k=1~n が独立事象かどうか分からんが、もし独立だとしたら
P_k = C[n,k] (1/2)^n
スターリングの公式
log(k!) ≒ (k+1/2)log(k) -k + (1/2)log(2π) + 1/(12k),
を使うと
log(P_k) = log(n!) - log(k!) - log((n-k)!) - n・log(2)
≒ -(1/2)log(π) - 1/(4n) -{2(n-1)/nn}(k-n/2)^2 -{4(n-3)/3n^4}(k-n/2)^4 - …
より
μ = n/2,
σ = n/{2√(n-1)},
k ~ Norm(n/2, n/{2√(n-1)}) いや、そこまで単純ではないと思う。
n=2のとき引かれた4つの玉をならべたら
| a1<b1 | a2<b2
AABB| ◯ | ◯
ABAB| ◯ | ◯
ABBA| ◯ | ✕
BAAB| ✕ | ◯
BABA| ✕ | ✕
BBAA| ✕ | ✕
でそれぞれ同様に確からしいわけでもないから、この表だけで独立でないとは言い切れないけど、独立かどうかはかなり怪しい。
2項分布二項分布B(n, 1/2)にはなると思うけど。
以下の性質をもつ実数xについての微分可能な関数f(x)の例を挙げるか、またはそのような関数が存在しないことを証明せよ。
・各自然数mに対しm-(1/m)≦x≦m+(1/m)の範囲において少なくとも1つの整数値をとる。
・任意の自然数kに対してある自然数a[k]が存在し、a[k]<x<a[k+1]の範囲でf(x)が自然数となるxがちょうどk個ある。
あれ?もしかして同様に確からしい?とすると一様分布になる?
>>398 n=100で1000万回シミュレーションしてみた。
結果は
> sd(re.sim) # シミュレーションの標準偏差
[1] 4.999704
> sqrt(n)/2
[1] 5
> n/2/sqrt(n-1)
[1] 5.025189
シミュレーション結果は√n / 2の方に近い。
正規分布近似でのパラメータを求めると
> (fit=fitdist(re.sim,"norm"))
Fitting of the distribution ' norm ' by maximum likelihood
Parameters:
estimate Std. Error
mean 50.001295 0.001581045
sd 4.999703 0.001117967
やはり、結果は√n / 2の方に近い
>>402 すみません書き間違えました
誤:a[k+1]
正:a[k]+1
>>401 2個の一様分布[0,1]をRで発生させて1個めを横軸、2個めを縦軸にしてグラフにしてみた。

一定の傾向はなさそうだから、独立のように見える。
ボケたレンズで見る。
縦に伸ばしてみる
横に縮めてみる。
いろいろ印象がかわり有意にみえるそうだよ。
むかし鳩の豆鉄砲撃ちデータなんて論文評価があったけどどうなったんだろ
>>405 それあってる?一様分布になると思うんだけど?
>>409 sim = function(n){
sum(runif(n) > runif(n))
}
re.sim=replicate(1e7,sim(n))
hist(re.sim,col='lightgreen',freq=FALSE,breaks=50)

>>409 ごめん。わからん。それn=2のとき結局4つの実数x1,x2,y1,y2とった後a1=min(x1,x2)、a2=max(x1,x2)、b1=min(y1,y2)、b2=max(y1,y2)の処理してる?
>>409 aの従う分布を
指数分布にしてもポワソン分布にしても、正規分布になるみたいだな。
>>411 すまん、あなたが正しい。ソートするのが抜けてた。
sim = function(n){
sum(sort(runif(n)) > sort(runif(n)))
}
re.sim=replicate(1e6,sim(100))
hist(re.sim,col='lightgreen',freq=FALSE,breaks=50)

aの従う分布を
正規分布、指数分布、ポワソン分布、負の二項分布、コーシー分布でやってみたが、どれも一様分布になった。
import Data.List
n = 30
samples = [ t | x1<-[1..n],x2<-[1..n],y1<-[1..n],y2<-[1..n],let s = nub $ sort [x1,x2,y1,y2],length s == 4, let [a1,a2] = sort [x1,x2],let [b1,b2] = sort [y1,y2],let t=[a1,a2,b1,b2]]
pl [a1,a2,b1,b2] = (if a1 < b1 then 1 else 0) + (if a2 < b2 then 1 else 0)
pls = map pl samples
main = do
print $ length $ filter (==0) pls
print $ length $ filter (==1) pls
print $ length $ filter (==2) pls
>>414 訂正
aの従う分布を
正規分布、指数分布、コーシー分布でやってみたが、どれも一様分布になった。
ポワソン分布、負の二項分布では一様分布にはならず。
>>413 だよね?一様分布になるハズ。
Haskell で n=30 で(値が被るときはのぞいて)ペア数0,1,2全部同数になる。
219240
219240
219240
コードは
>>415 というか一様分布になると証明出来たと思う。
方針は
>>415のコードでn=2、N=40で同数になったけど、n≧2、N任意で全部同数になる。
よってペア数=iである確率は1/(n+1)。
N→∞でも1/(n+1)。
>>416 SIM <- function(fun,n=100,...){
si = function(n,rfun=fun){
sum(sort(rfun(n)) > sort(rfun(n)))
}
re.si=replicate(1e4,si(n,fun))
hist(re.si,col=sample(colours(),1),...)
}
par(mfrow=c(3,3))
SIM(rnorm,main='正規分布')
SIM(rexp,main='指数分布')
SIM(rcauchy,main='コーシー分布')
SIM(function(x) rt(x,3),main='t分布')
SIM(function(x) rbeta(x,2,1000),main='β分布')
SIM(function(x) rgamma(x,2,1000),main='ガンマ分布')
SIM(function(x) rpois(x,7),main='ポアソン分布')
SIM(function(x) rnbinom(x,100,0.3),main='負の二項分布')
SIM(function(x) rbinom(x,100,0.1),main='二項分布')

う~ん、わからん。一様分布にならない分布もあるのか……
>>419-421 同じ値があることで、少なくカウントされているのなら
sum(sort(rfun(n)) > sort(rfun(n)))
を
sum(sort(rfun(n)) >= sort(rfun(n)))
にすれば、逆の分布になるのでは?
100回サイコロをふって1の目が出る回数は二項分布に従う。
それを30個ずつ乱数発生させてソートして配列順に大小比較して片方が大きかった総数をだす、
という操作を1000回繰り返して総数の分布をヒストグラムにする。
以下のコードを
https://rdrr.io/snippets/ に入力して実行する。
一様分布にはなっていない。
hist(replicate(1000,sum(sort(rbinom(30,100,1/6))>sort(rbinom(30,100,1/6)))))
hist(replicate(1000,sum(sort(rbinom(30,100,1/6))>=sort(rbinom(30,100,1/6)))))
で実行すると傾きが逆になりましたが一様分布とは言い難いようです。
離散分布だと同じ値が出るからでしょう。
ポアソン分布で特にそうなりやすいですね。
パラメータ7のポアソン分布で>と>=でやるには
https://rdrr.io/snippets/ に
hist(replicate(1000,sum(sort(rpois(30,7))>sort(rpois(30,7)))))
hist(replicate(1000,sum(sort(rpois(30,7))>=sort(rpois(30,7)))))
を入れるとグラフが出ます。
>>418 の方針では例えばn=2のときは任意の<j<k<lに対して
# ai<bi であるペア数
P(a1 = i, a2 = j, b1 = k, b2 = l) # 2
=P(a1 = i, b1 = j, a2 = k, b2 = l) # 2
=P(a1 = i, b1 = j, b2 = k, a2 = l) # 1
=P(b1 = i, a1 = j, a2 = k, b2 = l) # 1
=P(b1 = i, a1 = j, b2 = k, a2 = l) # 0
=P(b1 = i, b2 = j, a1 = k, a2 = l) # 0
が一様な離散分布のとき成立することを利用するんだけど、これ一様でない離散分布だと成立するとは限らないのかな? >>400
log(P_k) = log(n!) - log(k!) - log((n-k)!) - n・log(2)
≒ log(P_μ) - {1/(2σ^2)}(k-μ)^2 - {4(n-3)/3n^4}(k-μ)^4,
ここに
μ = n/2,
1/(2σ^2) = 2(n-1)/nn + 4/(3n^3),
log(P_μ) = - (1/2)log(nπ/2) - 1/(4n), パラメータ(平均=分散)7のポアソン分布4個を 20組だすとこんな感じ
> t(replicate(20,rpois(4,7)))
[,1] [,2] [,3] [,4]
[1,] 10 4 10 6
[2,] 5 7 5 7
[3,] 7 11 3 8
[4,] 8 4 8 2
[5,] 9 6 1 8
[6,] 5 10 9 7
[7,] 7 7 6 9
[8,] 8 7 7 7
[9,] 10 7 8 7
[10,] 4 12 13 10
[11,] 4 8 3 7
[12,] 7 6 7 8
[13,] 6 6 9 7
[14,] 7 7 10 9
[15,] 10 8 5 8
[16,] 7 7 7 8
[17,] 5 4 10 5
[18,] 7 9 5 4
[19,] 10 2 5 6
[20,] 8 11 5 8
>>428 n=2のときポアソン分布で20回やってみると
a1 a2 b1 b2 pair
5 7 6 8 0
a1 a2 b1 b2 pair
5 8 6 6 1
a1 a2 b1 b2 pair
8 9 4 7 2
a1 a2 b1 b2 pair
8 11 7 9 2
a1 a2 b1 b2 pair
6 10 4 5 2
a1 a2 b1 b2 pair
4 8 4 6 1
a1 a2 b1 b2 pair
6 6 8 8 0
a1 a2 b1 b2 pair
8 8 6 9 1
a1 a2 b1 b2 pair
4 7 4 9 0
a1 a2 b1 b2 pair
9 9 4 13 1
a1 a2 b1 b2 pair
6 10 8 8 1
a1 a2 b1 b2 pair
6 8 5 8 1
a1 a2 b1 b2 pair
5 9 6 7 1
a1 a2 b1 b2 pair
6 7 3 5 2
a1 a2 b1 b2 pair
5 12 9 10 1
a1 a2 b1 b2 pair
6 12 6 8 1
a1 a2 b1 b2 pair
5 5 4 10 1
a1 a2 b1 b2 pair
6 13 6 11 1
a1 a2 b1 b2 pair
6 15 9 13 1
a1 a2 b1 b2 pair
11 13 4 5 2
> c(pair=pair)
pair1 pair2 pair3 pair4 pair5 pair6 pair7 pair8 pair9
0 1 2 2 2 1 0 1 0
pair10 pair11 pair12 pair13 pair14 pair15 pair16 pair17 pair18
1 1 1 1 2 1 1 1 1
pair19 pair20
1 2
> table(pair)
pair
0 1 2
3 12 5
全然、一様分布になっていない
Rってぱっと書けるために可読性をかなり犠牲にしてるね。
さっぱりわからん。
ポアソン分布は非負整数を返してくるから、その値にゆらぎをつけて同値が起こらないようする(Rではjitterという関数)と
例
a1 a2 b1 b2 pair
3.94 5.02 11.06 13.51 0.00
a1 a2 b1 b2 pair
7.06 11.19 7.87 7.99 1.00
k=10000
pair=NULL
for(i in 1:k){
a=sort(jitter(rpois(2,7)))
b=sort(jitter(rpois(2,7)))
c=sum(a>b)
pair[i]=c
}
hist(pair,col='skyblue')
このポアソンもどき分布での結果は、一様分布。

>422
の御指摘のように
離散分布で成立しないのは同値の存在のため。
自分には原因がわからなかったので>422の指摘は目から鱗でした。ありがとうございました。
>>398解くのに図1の左下から右上に至る最短経路ρに対して=を通る回数を X(ρ) とすると i:0~n に対して X(ρ) = i となる経路の数がカタラン数 C[n] になること使ったんだけど、こんなん知らんかった。
C[n] = C[2n,n]/(n+1) の n+1 の意味を初めて知った。
―図1―(n=6の場合)
┌─┬─┬─┬─┬─┬─┐
│ │ │ │ │ │ │
├─┼─┼─┼─┼─┼=┤
│ │ │ │ │ │ │
├─┼─┼─┼─┼=┼=┤
│ │ │ │ │ │ │
├─┼─┼─┼=┼=┼=┤
│ │ │ │ │ │ │
├─┼─┼=┼=┼=┼=┤
│ │ │ │ │ │ │
├─┼=┼=┼=┼=┼=┤
│ │ │ │ │ │ │
└=┴=┴=┴=┴=┴=┘
ノートにまとめてみたけどやっぱり
>>398は特に一様分布である必要はなくて非特異(=分布関数が連続)であるIID(独立同分布)であればイイ(ペアの個数は一様分布になる)はず。
小さい順にという縛りをなくして
乱数をn個発生させて,a(1), ..., a(n)とする。
同様にもう一度n個の乱数を作ってb(1), ..., b(n)とする。
a(1)とb(1), a(2)とb(2), ...と乱数発生順にペアを作り大小を比較する。
この時aのほうが大きいペアの数は0個~n個のいずれかになるが,その確率分布は?
という問題にすると、乱数発生の分布が離散分布であっても、ペアーの個数の分布は正規分布になるみたい。
シミュレーションでの結果。
多分、中心極限定理のおかげかな。大小比較なので乱数発生がコーシー分布でもいいみたい。
一様分布ならどうなる?二項分布なら?……
計算機はなんでも答えてくれるけど、逆になんでも答えてくれるから頭使わなくなるんだな……
>>398 p(1),…,p(n),q(1),…,q(n)を非特異(=分布関数が連続)な独立同分布な確率変数とし、それぞれを昇順に並べたものをa(1),…,a(n),b(1),…,b(n)とする。
a(i) < b(i)となる i の個数をNとする。
このときNの分布は一様分布である。
(∵)
a(1)~b(n)共通の分布関数をFとする。
a(1),…,a(n),b(1),…,b(n)すべてを昇順に並べたものをc(1),…,c(2n)とする。
MをAをn文字、Bをn文字、計2n文字を並べたものの全体とする。
Mに値をとる確率変数μを
μ[i] = A ⇔ c(i) = a(k) (∃k)、μ[i] = B ⇔ c(i) = b(k) (∃k)、
で定める。
m∈Mに対し A[m] = μ^(-1)(m) とおく。
Gを{1,2,…,n}の置換の全体としg,h∈Gに対し
B[gh] = {ω| a[i] = p[g(i)], b[i] = q[h(i)]}
とおく。
長さ4nの狭義単調増大列の全体をVとし、v∈Vに対し
C[v] = {ω|v[2i-1] < c[i] <v[2i]}
とおく。
このとき任意のμ、μ'、g、h、vに対し
P(A[μ] ∩ B[gh] ∩ C[v]) = P(A[μ'] ∩ B[gh] ∩ C[v]) = Π(F(v[2i]) - F(v[2i-1]))
である。
任意のv',v''に対しC[v']∩C[v'']は空でなければC[v']∩C[v'']=C[v]となるvがとれることとσ加法性により
A[μ] ∩ B[gh] = A[μ'] ∩ B[gh]
である。ことなるg,hの組に対しB[gh]は互いに排反であるから足し合わせて
A[μ] = A[μ']
である。
Mの各元 m に対し
L(m) = #{i | mの中のi番目のAがi番目のBより前}
とおくと
N(ω) = L(μ(ω))
であるから
P(N = k) = #{m∈M | L(m) = k}/C[2n,n]
である。
ここで任意のkに対し#{m∈M | L(m) = k}はカタラン数C[2n,n]/(n+1)に等しいから主張は示された。
>>439 訂正
✕:A[μ] ∩ B[gh] = A[μ'] ∩ B[gh]
◯:P(A[μ] ∩ B[gh]) = P(A[μ’] ∩ B[gh])
✕:A[μ] = A[μ']
◯:P(A[μ]) = P(A[μ’])
『辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には、
周の長さも面積も共に等しい組が(相似を除いて)たった 1 組しかない』
これ、問題はシンプルなんだけど初等的な方法では解けないそうだ
まるでフェルマーの大定理みたいで面白い
>>441 こういう事?
(直角三角形Ver)
a,b,c,a’,b’,c’が正の整数、a^2 + b-2 = c^2、 a’^2+b’^2 = c’^2、ab = a’b’、a+b+c = a’+b’+c’ ⇒ (a,b,c) =(a’,b’,c’)
(二等辺三角形Ver)
a,b,,a’,b’が正の整数、2a > b、 2a’ > b’ 、b√(a^2-(b/2)^2) = b’√(a’^2-(b’/2)^2) 、2a+b= 2a’+b’⇒ (a,b) =(a’,b’)
いやこうか
a+b+√(a^2+b^2) = 2c + d
(1/2)ab = (1/2)d√(c^2 - d^2/4)
2c>d
をみたす正の整数a,b,c,dの組は一組しかない。
>>444 この記事の
>種数1以上の代数曲線上の有理点集合の決定」に帰着される問題には、現代でも統一的な解法が知られていない。
これあってる?
種数1=楕円曲線の場合には一応アルゴリズムが発見されてた希ガス。
>>443
ピタゴラス数より
a = kk-LL,
b = 2kL,
c = 6(mm+nn),
d = 12(mm-nn),
とおく。
周長/2: k(k+L) = 12mm,
面積: kL(kk-LL) = 6(mm-nn)・12mn
辺々割ると
L(k-L) = 6(mm-nn)n/m,
これらを満たす正の整数の組は
(k, L, m, n) = (16, 11, 6, 5)
しかない…
(a, b, c, d) = (135, 352, 366, 132) とある会社の社長は毎日午後5時に会社を出て自宅からの迎えのクルマに乗って帰る。
ある日、午後4時に退社した。
天気が良かったので、迎えのクルマに出会うまで散歩した。
出会ったところで、クルマはUターンして自宅に戻った。
するといつもより10分早く帰宅した。
何時何分にクルマに出会ったか?
https://cybozushiki.cybozu.co.jp/articles/m000434.html 「接近する2人の間を往復し続ける犬が走る距離」の問題のような、面白い発想の解答が存在する…?
成立学園1-F担任の岩崎柾典先生がヤバイ。
成立学園に勤めるのは3年目。
担当科目は数学。
部活は女子テニス部。
何がヤバイというと、2013年4月から2015年3月まで宮前平中に働いていたけど、女子中学生とsexしたことがバレて、飛ばされたから。
今でも教師を続けているのがすごく不思議な感じだよ。
岩崎先生って、ツイッターとFacebookをやってるみたいだから、覗いてみては?
https://m.facebook.com/masaoki.iwasaki.9 https://twitter.com/mas20285 https://twitter.com/keepmathtop https://twitter.com/kyuuchan_ https://twitter.com/xPuGPq8Tn9GWCJb https://twitter.com/K46_N700_hikari 







今度はこの問題を解いてみて?
https://twitter.com/5chan_nel (5ch newer account)
>>448 d:全距離
c:車速
w:歩行速度
t:歩行時間
{5+d/c} - {4+t+(d-wt)/c}=10/60
t = (5 c)/(6 (c - w))
ここから進めなくなった。
>>448 いつもより50分帰宅に使う時間が長かった。
つまり社長は50分いつもより長く散歩ができたと喜ぶはずだ、と家から来た頭のいい家来のクルマは計算しいつもより10分早く帰宅するよう走った。
社長は4:00に会社を出たから、クルマと出会ったのは4:50。
~ 人人 ~今日は
~ (_(_)4時あがり
ε(^o^)) だったから
~∩ξ_ノ散歩したよ
(e`) ) )゙わっはっは
UyU⌒Uヾ, ……
~υυ`υυ...カッポカッポ
>>453 社長の歩行時間と歩行速度は関係ない。
散歩した距離 l だけが問題。
ピックアップした時間は5時からl/cだけ前。
通常の車の走行時間 - その日の車の走行時間 = 2d/c - 2(d-l)/c = 1/6。
l/c = 1/12。
まぁ、ちょろっと鉄道のダイアグラム風の図かけば 4:55 なのはすぐわかるけど。
社長と車は同時に出発という暗黙の条件があるので
d:全距離
c:車速
w:歩行速度
t:歩行時間
wt+ct=dが加わるかな。
d:全距離
c:車速
w:歩行速度
t:歩行時間
l:歩行距離
l=wt
車の走行時間差から
l/c=wt/c=1/12
を
{5+d/c} - {4+t+(d-wt)/c}=10/60
に入れると
t=1+1/12-10/60=55/60社長は55分歩いた。
難しく考えすぎ。
10分早く帰宅できたってことは、車が会社のビルから片道5分の距離だけ家に近いところで社長を拾っただけのこと。
OK?
>>448 帰宅時刻がいつもより10分早かったという意味?
それとも帰宅に要した時間が10分短かったという意味?
普段は5時に車で帰って7時に自宅到着
今回は4時に歩いて出発、途中から車で自宅到着が6時50分という意味に解釈したんだが、
題意は帰宅に要した時間が10分短い5時50分に自宅到着という意味なのか?
まぁ問題の設定があまりにも非現実的なのも一因かな?
帰りの車が毎日自宅からピッタリ社長の退社時間5:00に会社につくように迎えにくるという設定みたいだけど、実際にそんな事するやつおらんと。
>>448 問題文からは、通常時、五時にクルマに乗っているとは、確定しきれない。つまり、
>>とある会社の社長は毎日午後5時に会社を出て自宅からの迎えのクルマに乗って帰る。
を、「とある会社の社長は毎日午後5時に会社を出て(自宅に向かって歩き出し、その途中)
自宅からの迎えのクルマに乗って帰る。」の様に受け取ることも可能。
「いつもは、5時にスタートする散歩がてらの帰途を、この日は4時にスタートした。(中略)
さて、クルマに乗った時刻は?」
のような問題とも受け取れる。このような解釈をした場合、クルマに乗ったのが4:55とは確定されない。
ただ、社長はいつもより五分早くクルマに乗ったということは言える。
>>465 通常時は5時には車が会社で待っていてそれに乗って帰るでいいんだが、
10分早く帰宅
の意味が時刻なのか帰宅所要時間なのか判然としない。
5時に歩き始めたでなくわざわざ4時に出発なのでどちらともとれる。
>>466 車の方が徒歩より早いので
所要時間でなく到着時刻が10分早いというのが題意じゃないかな?
帰宅時間のうち車に乗っていた時間が10分短いという意味ではないと思う。
>>466 まず、一番最初にいっておかなければならないが、
普通に解釈すれば、通常は5時にクルマに乗るのだろうし、
帰宅した時刻が10分早かったのであって、所要時間が10分短かったのではないことは
(AIだったら難しいかもしれないが、)人間だったら判る。
あえて、問題にいちゃもんをつけて、楽しんでいることを共通認識にしたいと思う。
>> 10分早く帰宅
>>の意味が時刻なのか帰宅所要時間なのか判然としない。
これは、クルマだけで帰宅するより、散歩+クルマで帰宅した方が、帰宅所要時間が
短かったということを、解釈の選択肢に加えなければならないという事ですよね?
つまり、
散歩の速度 > クルマの速度
を想定していると。(
>>463の説明だと、これですよね)
徒歩より、自転車の方が速いし、自転車より、自動車の方が速いのは、小学校でも暗黙の了解だとおもいます。
もし、散歩+クルマで要した時間ではなく、クルマだけで要した時間が10分短かった というような設定の問題
ならあり得ますが、問題文を読む限り、このような設定ではないし...。
10分早いというのは、時刻であって、所要時間とするのは、厳しいかと。
>>468 時刻での計算が
d:全距離
c:車速
w:歩行速度
t:歩行時間
{5+d/c} - {4+t+(d-wt)/c}=10/60
t = (5 c)/(6 (c - w))
まではいいのだが
車の往復走行時間の差が到着時刻の差になるという理由がわからないで困っている。
>>469 c/wでもわからないと歩行時間は確定できないのじゃないかという
最初の疑問、>453に思考が戻ってしまったわけです。
ダイヤグラムを書くと
普段
A クルマ自宅発
B クルマ会社着=クルマ会社発
C クルマ自宅着
その日
A' クルマ自宅発=A
B' クルマ社長乗せてUターン
C' クルマ自宅着
条件
クルマの速さは至るところ同じと仮定すると、
ABとBCの長さは等しい
AB'とB'C'の長さは等しい
△ABCと△AB'C'は相似
Bの座標は時間成分は5時
CC'=10分
さて、B'の時刻は?
>>471 クルマが同じ時刻に自宅から迎えに出発という前提はないんじゃない?
通常、早めに出発して5時に会社で待機するだろ?
迎えの車は5時に到着するという暗黙の条件があったのだな。
帰りの時間だけ考えていたから答がみつからなかったのだな。
ようやく納得できました。
前
>>454 求める社長とクルマの出会う時刻を4時x分とする。
クルマが自宅会社間y㎞を時速v㎞で等速直線運動する場合、クルマは自宅から会社まで(y/v)時間、往復だと(2y/v)時間いつも走ったはる。
今日クルマはいつもどおり社長を迎えにいったが、自宅から(vx/60)㎞地点で思わず散歩したはる社長に遭遇、「社長、どないしはりましたん!?」
「かくかくしかじか」話は帰りの車の中で、ということで題意よりじきUかましましたんですが、結果的に家にいつもより10分はよ着いたという話。 クルマは(日いいいもと違っては、
)y/v-10/60㎞時間走ったわけだけど、そのちょうど半分の時間で社長に出会ったんで、
(2y/v-10/60)(1/2)=x/60
y/v-5/60=x/60
60y/v=x+5
クルマがいつもどおり時速60㎞で等速直線運動したと仮定すると、
y=x+5
会社から自宅まで55㎞歩いて帰るのはきつい。
x=50(分)
これ以上は特定のしようがない。
a,bを正の定数、x,yを正の実数とするとき
a*(x^2)+b*(y^2)が最小になるのは
x+yが最小になるときである。
↑これって正しいですか?証明すると結構ながくなりますか?
車に着目したら簡単。
浮いた10分は社長に逢った地点から
会社までの往復分なんだから。
その片道は5分だから、
会社到着予定時刻の5分前に社長に逢った。
>>478ああ、そうだ。それ正解だと思う。
訂正。前
>>475 求める社長とクルマの出会う時刻を4時x分とする。
クルマが自宅会社間y㎞を時速v㎞で等速直線運動する場合、クルマは自宅から会社まで(y/v)時間、往復だと(2y/v)時間いつも走ったはる。
今日クルマはいつもどおり社長を迎えにいったが、自宅から(vx/60)㎞地点で思わず散歩したはる社長に遭遇、「社長、どないしはりましたん!?」
「かくかくしかじか」話は帰りの車の中で、ということで題意よりじきUかましましたんですが、結果的に家にいつもより10分はよ着いたという話。
クルマは今日はいつもと違って、
(2y/v-10/60)時間走ったわけだけど、そのちょうど半分の時間で社長に出会ったんで、
(2y/v-10/60)(1/2)=x/60
y/v-5/60=x/60
60y/v=x+5
クルマがいつもどおり時速60㎞で等速直線運動したと仮定すると、
y=x+5
会社から自宅までは50㎞。x=55(分)
これはありえる。
出会った地点から会社までの距離は、
y-vx/60
社長はx/60時間歩いたから、社長の歩く速さは、
(y-vx/60)÷(x/60)=60y/x-v
4時x分(x/60時間後)、社長は会社から、
(60y/x-v)×x/60=y-vx/60 (㎞)の地点を歩いたはった。
>>471 ご丁寧に解説いただいたので、グラフにしてみました。

>>479 時速30kmだったり、道路が曲線だったら計算変わる?
>>481時速30㎞は遅いね。パパァー!! 鳴らされっで。道は曲線でもいいけど。前
>>479 つまりクルマの時速とか自宅会社間の距離とかどうでもいいわけか。
まとめると、
いつもより10分はよ着いたクルマは社長と出会わなんだら社長と出会った地点から会社まで10分で往復できたはず。クルマが社長と出会ったのは会社到着予定時刻5:00(待ち時間なし)の5分前。
∴4:55
>>482 社長が乗ってないときは時速60kmで社長が乗ったら時速30kmにすると面白いかも。
>>483 こんなダイヤグラムになるな

l:歩行距離
迎えの車速:rv
同乗の車速:v
通常:d/rv+d/v
早退:(d-l)/rv+(d-l)/v
d/rv+d/v - ((d-l)/rv+(d-l)/v)= 10/60
l (r + 1)/rv=10/60
l/v=10/60*r/(r+1)
5+d/v - {4+t+(d-l)/v}= 10/60
1-t+l/v=10/60
t=50/60+l/v=(50+10*r/(r+1))/60
迎えの車速が社長同乗時のr倍とすると
社長の歩いた時間は
50+10*r/(r+1) 分
t:歩行時間
l:歩行距離
迎えの車速:rv
同乗の車速:v
通常走行時間:d/rv+d/v
早退時走行時間:(d-l)/rv+(d-l)/v
d/rv+d/v - ((d-l)/rv+(d-l)/v)= 10/60
l (r + 1)/rv=10/60
l/v=10/60*r/(r+1)
5+d/v - {4+t+(d-l)/v}= 10/60
1-t+l/v=10/60
t=50/60+l/v=(50+10*r/(r+1))/60
迎えの車速が社長同乗時のr倍とすると
社長の歩いた時間は
50+10*r/(r+1) 分
>>483実際そんなもんかも。午後4時台はわりと進むと思うけど午後5時台の下りは混む可能性が高い。速度半分はかなりリアルですね。前
>>482 >>484 ABの傾きが60
BCの傾きが-30
CC'=10/60のときHH'を求めよという幾何の問題になるな。
どうすれば簡単に求まるだろ?
>>487 リアルさでいうなら、社長は早く帰宅しなければならない用事ができた。
5時に到着するようにクルマが会社に向かっている、社長は自宅に向かって歩きだした
4時30分にクルマと合流した、いつもより何分早く帰宅できるか?
こういう方が現実にはありそう。
>>489 >486の式の10/60をXに置き換えて
社長の歩行時間をt hourとすると
X= (r + 1) (1- t ) hour早く到着。
>>489一時間余裕が生まれたから健康と気分転換のために散歩しよう、電源切って。前
>>487このほうが社長らしいと思います。
どのような非負整数a,b,cに対しても、下記の方程式を満たす非負整数m,nが存在すると言えるか。
a(m+bn)-cn^2=1
>>492 訂正
正しくはam(m+bn)-n^2=1
>>490 一般化してみた。
歩行時間:t
歩行距離:l
迎えの車速:rv
同乗の車速:v
出発時刻差:s
到着時刻差:X
通常走行時間:d/rv+d/v
早退時走行時間:(d-l)/rv+(d-l)/v
d/rv+d/v - ((d-l)/rv+(d-l)/v)= X
l (r + 1)/rv=X
l/v=X*r/(r+1)
s0+s+d/v - {s0+t+(d-l)/v}= X
s-t+l/v=X
X=(r + 1) (s - t)
t = (r s + s - X)/(r + 1)
xyz空間の4点
O(0,0,0),A(1,0,0)B(0,1,0)C(0,0,1)
を頂点とする四面体Vがある。
Vの内部で、領域
2x≧2y^2-1かつ3z≧x^2-2
の内部にもある部分の体積を求めよ。
>>492-493 方程式 x^2+abx-a =0 の解をα,βとしQ(α) = Kとおくと
N(n+mα) = (n+mα)(n+mβ) = n^2 - abmn - am^2。
よってKの基本単数をεとするとき
∃m n n^2 - abmn -am^2 = -1 ⇒ N(ε) = -1。
ここで a=2、b=1のときK=Q(√3)でありε=2+√3、N(ε) = 1ゆえ与式は解を持たない。
別スレより
Aをn次交代行列とする。det(A) をその行列式、Pf(A) をPfuffianとする。
このとき
det(A) = Pf(A)^2
を示せ。
https://ja.wikipedia.org/wiki/%E3%83%91%E3%83%95%E3%82%A3%E3%82%A2%E3%83%B3 だいたい前スレからの流れだと、これ以上待っても答え出そうになさそうなタイミングで自分が解答貼るのが通例だな。
>>495 V=1/6
正四面体は0≦x≦1の範囲にある。
一方、3z≧x^2-2のx軸上の範囲は、
z=(x^2)/3-2/3のグラフより、
0≦x≦√2
z軸について下に凸だから 、
3z≧x^2-2の領域は正四面体Vを包含する。
同様にx=y^2-1/2のグラフより、
求める物体は正四面体Vを放物面x=y^2-2で切りこみ、x<y^2-1/2の部分を切りとったもの、すなわちy=0の平面からy=1/√2の平面までは三角錘台として求め、y=1/√2の平面からy=(√7-1)/2の平面まではy=tで水平に切った切り口の面積の和として求める。
具体的にはその区間で微分して積分する。
三角錘台は1/6-1/6(1-1/√2)^3
積分区間のy=tにおける断面積は、
1/2(1/2-t^2)^2
積分区間を表す括弧を【】にすると、
(求める物体の体積)=1/6-1/6(1-1/√2)^3+(1/2)∫【1/√2~(√7-1)/2】(1/2-t^2)^2}dx
1/6-1/6(1-1/√2)^3+(1/2)∫【1/√2~(√7-1)/2】(1/2-t^2)^2}dx
=(5√2+6)/24+(1/2)[t/4-t^3/3+t^5/5]【1/√2~(√7-1)/2】
=……ひたすらべつに面白くもない計算をし、
通分して表すと、
=(50√2+1453√7-3757)/240
直方体ABCD-EFGHにおいて、
(△BDE)^2=(△ABD)^2+(△ADE)^2+(△AEB)^2
が成り立つことを示せ
(ただし、△BDEなどはその三角形の面積を表す)
正八面体の投影図が六角形となる必要十分条件を求めよ。(ただし平行四辺形の辺上に点が存在するものは平行四辺形とする)
前
>>500訂正。
放物面x=y^2-1/2
(-2じゃなく-1/2)予測変換してしまうんで。
>>501 4面体ABDE で考える。
△BDE = (1/2)|↑BD×↑BE|,
を求める。
A (0, 0, 0)
B (b, 0, 0)
D (0, d, 0)
E (0, 0, e)
とおくと、
↑BD = (-b, d, 0)
↑BE = (-b, 0, e)
(1/2)↑BD×↑BE = (de/2, eb/2, bd/2) = (⊿ADE, ⊿AEB, ⊿ABD)
これより求める関係が出る。
なお、(1/2)↑BD×↑BE = △BDE ↑n,
↑n は平面BDEの法線単位ベクトル。
もちろん、DE^2 = x, EB^2 = y, BD^2 = z とおいてヘロンの公式
S = (1/4)√{2(xy+yz+zx) -xx -yy -zz},
を使ってもできます。
>>501 △BDE、△ABD、△ADE、△AEBの単位法線ベクトルをそれぞれn、e、b、d、平面BDEへの射影像の面積をS、Se、Sb、Sdとする。
△ABD = (ne)△BDE、△ADE = (nb)△BDE、△AEB = (nd)△BDE
により
与式右辺 = ((ne)^2 + (nb)^2 + (nd)^2)(△BDE)^2 = (△BDE)^2 = 与式左辺 (∵ n は単位ベクトルで(e,b,d)は正規直交規定)。
>>504カブスマ
>>505 間違いじゃないが
>平面BDEへの射影像の面積をS、Se、Sb、Sdとする。
はいらなかった。
>>497 nが奇数なら0、nが偶数のときはパフィアンの2乗になる。
分かスレ446 939-944 を参照。
>>504,505
明快ですね
自分が用意してたのは、
>>504のように頂点の座標を決めて
△BDEを含む平面x/b+y/d+z/e=1と原点との距離を求め、
四面体ABDEの体積を2通りに表す、という方針でした
1/6=0.166……>(50√2+1453√7-3757)/240=0.6……
おかしい。間違ってる。
前
>>503 前
>>509y=tで切った切り口の面積が違った。やりなおしたい。時間をくれないか。
>>507 そうです。それを証明して下さいが題意。
wikipediaに載ってる定義どうりにやって力押ししてもできるかもしれませんが、用意の解答は一工夫しました。
自然な問題なのでいろんな面白いルートがありそう。
nを2以上の自然数としる。
1~nの自然数を小さい方から並べた順列 1,2,3,……,n を、
次の操作1 or 操作2 を繰り返して n,n-1,……,2,1と逆順にしたい。
[操作1] 隣接する2項を入れ替える。
[操作2] 隣接する3項 x, y, z について(yはそのままで) xとzを入れ替える。
操作を行う必要回数をa[n] とおく。この a[n] を求めたいのです。
例えばn=4のときは
1234 → 3214 →3412 → 4312 → 4321 で4回で行けそうです。
調べると a[2]=a[3]=1, a[4]=a[5}=4, a[6]=a[7]=7, a[8]=14 になるみたい(自信無し)なのですが
一般項は求められるでしょうか。漸化式でも分かればいいのですが。
宜しくお願いします。
前
>>510 正四面体(V=1/6の三角錘)に放物曲面x=y^2-1/2の切れ目を入れる。点B(0,1,0)を含む一角をとりのぞくだけだから、求める体積は0.15ぐらい。
0≦t≦1/√2の値をとるxy平面と平行な平面z=tで切った切り口の面積をtで表す。
0≦y≦1/√2の範囲は切り口が平面だから角錐台として体積V1を求める。
1/√2≦y≦(√7-1)/2の部分を微分積分。
体積V2=∫【1/√2~(√7-1)/2】{(1-t)-(t^2-1/2)}dt
V1=(1/√2)(1-1/√2)+(1/2)(1/√2)^2+……
(つづく)
色んなやり方ありますがたとえば
123456 → 132456 → 132465 → 136425 → 631425 → 634125 → 634521 → 654321
どの面も出るのが同様に確からしい8面ダイスを
独立に2回振った時に少なくとも一回は4の目が出る
確率はいくらですか?
1..2..3..4..5..6.7..8
1■■■□■■■■
2■■■□■■■■
3■■■□■■■■
4□□□□□□□□
5■■■□■■■■
6■■■□■■■■
7■■■□■■■■
8■■■□■■■■
一回目i,二回目jとして
Ω={(i,j)|1≦i≦8,1≦j≦8}から
#A=64-49=15なので
少なくとも一回は4の目が出る確率は
P(A)=15/64ですか?
次の行列式を計算し、因数分解せよ。
determinant{{ax, az+cx, cz}, {ay+bx, aw+dx+bz+cy, cw+dz}, {by, bw+dy, dw}}
>>516 なるほど。
なんか Coxeter Group の reduced expression の理論とかいうのがあるらしいけどそれ使えないのかな?
>>519 (%i1) determinant(matrix([a*x,a*z+c*x,c*z],[a*y+b*x,a*w+d*x+b*z+c*y,c*w+d*z],[b*y,b*w+d*y,d*w])),factor;
(%o1) (a*d-b*c)*(b*z+c*y-d*x-a*w)*(y*z-w*x)
前
>>515 z=t平面の切り口の面積を、
0≦t≦1/√2の範囲で積分し、あとの部分は三角錘台として求める。
z軸に垂直な面でスライスすれば、積分区間は0~1/√2でいいことに気づいた。
放物曲面の屋根がついた部分=∫【0~1/√2】{(1-t)-t^2-1/2)dt
=[3t/2-t^2/2-t^3/3]【0~1/√2】
=(2√2)/3-1/4
三角錘台=1/6-1/2√2
V=(2√2)/3-1/4+1/6-1/2√2
=0.152368927……
あってる。
前
>>522 通分したかたちで表すと、
V=(2√2)/3-1/4+1/6-1/2√2
=(5√2-1)/12
≒0.5……
あってない。Googleの演算順序が読みちがえていい値になっただけ。
>>508 頂点Aから平面BDEまでの距離をhとする。
4面体A-BDEの体積Vは
V = (b/3)⊿ADE = (d/3)⊿AEB = (e/3)⊿ABD = (h/3)△BDE,
(右辺) = (⊿ADE)^2 + (⊿AEB)^2 + (⊿ABD)^2 = (3V/b)^2 + (3V/d)^2 + (3V/e)^2,
(左辺) = (△BDE)^2 = (3V/h)^2,
ところで h = 1/√(1/bb + 1/dd + 1/ee) だから成立。
>>524
[ax, az+cx, cz]
[ay+bx, aw+bz+cy+dx, cw+dz]
[by, bw+dy, dw]
||
[a, c, 0, 0] [x, z, 0]
[b, d, a, c] [0, x, z]
[0, 0, b, d] [y, w, 0]
[0, y, w]
||
[a, 0, c, 0] [x, z, 0]
[b, a, d, c] [y, w, 0]
[0, b, 0, d] [0, x, z]
[0, y, w]
では 出ませぬ^^ >>526 結果から、行列の積に書き直してからdet計算するのかと思ったけど、3次行列だった…。
>>526 の続き
[a, c, 0, 0]
[b, d, a, c]
[0, 0, b, d]
の任意の3列からなる正方行列は、1行目 or 3行目の非0成分が1個だけで
[a, c] = ad-bc
[b, d]
を因子にもつ。
同様に
[x, z, 0]
[y, w, 0]
[0, x, z]
[0, y, w]
の任意の3行からなる正方行列は、1列目 or 3列目の非0成分が1個だけで
[x, z] = wx-yz
[y, w]
を因子にもつ。
∴ (ad-bc) ( ????? ) (wx-yz) の形になるのは分かるが…
次の行列式を計算し、因数分解せよ。
determinant{{a, b, c, 0}, {y, x, 0, -c}, {z, 0, -x, -b}, {0, -z, -y, -a}}
これも手計算は無理?
積分する区間をもっと限定できる。前
>>523 P(0,1/√2,0)
Q(0,1/√2,1-1/√2)
R(1-1/√2,1/√2,0)
S((3-√7)/2,(√7-1)/2,0)
T((3-√7)/2,1/√2,0)
物体PQRSのうち、放物曲面PQSを持つ物体PQSTの部分のみ微分積分する。
(つづく)
>>530 それは1列目と4列目、2列目と3列目ひっくり返して
>>497でいける。
>>514,520
あかん。s[1]=(12)、…、s[n-1]=(n-1 n)、t[1]=(13)、…t[n-2]=(n-2 n)で(s[i]s[i+1])^3 = 1、(s[i]t[i])^3=1、…全部いれてもCoxter Systemにならん。
なのでもちろん reduced expression の理論もつかえない。
なので解けるにしても一般論は使えず、ゴリゴリやるしかなさそう。
座標を整理する。
P(0,1/√2,0)
Q(0,1/√2,1-1/√2)
R(1-1/√2,1/√2,0)
S((3-√7)/2,(√7-1)/2,0)
T((3-√7)/2,1/√2,0)
放物曲面を平面z=tで切ったときのQSとの交点をUとすると、
U((3-√7)t/(2-√2)+(3-√7)/2,√(t+1/2),t)
三角錘台PQR-OCA=1/6-1/6(1-1/√2)^3
=(7√2)/24-1/4――①
三角錘台PQR-OCAより上の部分のうち平面のみで囲まれた部分QRST=(1/3)(1/2){1-1/√2-(3-√7)/2}{(√7-1)/2-1/√2}(1-1/√2)
=(1/6)(√7-√2-1)/2}{(√7-√2-1)/2}{(2-√2)/2}
=(8-3√2-√14)/48――②
三角錘台PQR-OCAより上の部分のうち放物曲面PQSの屋根を持つ部分=∫【0~1-1/√2】(3-√7)t/(2-√2)+(3-√7)/2-(t^2-1/2)}dt
=∫【0~1-1/√2】{(3-√7)t/(2-√2)+(4-√7)/2-t^2}dt
=[(4-√7)t/2+(3-√7)t^2/2(2-√2)-t^3/3]【0~1-1/√2】
=35/12-(19√2)/24-(7√7)/4+(3√14)/4――③
①+②+③=17/6-(27√2)/48-(7√7)/4+(35√14)/48
=0.136065255……
前
>>531頂点B付近を意外と大きくえぐってくるな。
問題
>>495禿げたくない。
>>514,529
a[7]=7 にはならない。なぜなら、
順列7654321は転倒数が21であり、操作1,2は転倒数を高々それぞれ1,3しか増加させないので、
操作数が7なら、すべて操作2でなくてはならないが、この場合、互いに独立した1357と246の隣接互換での操作に等しい。
それぞれ7531と642にする操作数は、それぞれ6,3なので、合わせて9となり、矛盾する。
また、順列7654321は置換として奇置換であり、操作1,2も奇置換であるから、操作数は奇数。
したがって、上のすべて操作2の場合が最小となり、a[7]=9。
PCにやらせた結果も、a[7]=9。
PCの結果は、a[2]=a[3]=1, a[4]=a[5]=4, a[6]=7, a[7]=9, a[8]=14, a[9]=16。
(a[9]=16 出すのに数時間かかった。)
>>514 根拠は薄弱だが、下のような n-1個から始まる階段状の○に
┏━を最大限敷き詰めたときの、
┃
┏━と○の個数の合計が、a[n]であると予想する。
┃
n=8の場合:
○○○○○○○
○○○○○○
○○○○○
○○○○
○○○
○○
○
に最大限敷き詰めて、
┏━┏━○┏━
┃○┃┏━┃
┏━○┃○
┃○┏━
┏━┃
┃○
○
で、a[8]=7+7=14。
これがもし正しいなら、n=2k+1のとき a[n]=k^2、n=2kのとき a[n]=k^2 - 2[(2k-1)/5]。
ただし、[]はガウス記号(floor関数)。
実際 n=16のとき上の式で a[16]=64-6=58 であるが、下のように58回でできる:
(56)(45)(67)(34)(56)(78)(bc)(ab)(cd)(8a) (68)(ac)(46)(8a)(ce)(24)(68)(ac)(ef)(12)
(46)(8a)(ce)(fg)(24)(68)(ac)(ef)(46)(8a) (ce)(68)(ac)(8a)(34)(56)(78)(45)(67)(56)
(ab)(cd)(bc)(13)(35)(13)(24)(ce)(eg)(ce) (df)(78)(ab)(8a)(68)(89)(9b)(79)。
ここで、()は互換(操作1,2を表す)で、10~16をa~gとした。
最小回数であることは確かめていない。(簡単にできる方法ある?)
しかし穴埋め問題なんて見りゃわかるだろうさ。独りよがりでない事。
不自然さを競うなよ。理系頭脳は秩序だったフィクションだと世界を気付かない。
>>536 その “敷き詰め” から逆順に持っていく “置換” はどう対応してるんですか?
あ、わかった┌が一個飛びの置換で◯が隣接する置換か。
でもその “敷き詰め” の “┌” と “◯” の合計が
>n=2k+1のとき a[n]=k^2、n=2kのとき a[n]=k^2 - 2[(2k-1)/5]
になるのは何故ですか?
正八面体Kの各辺の中点を通る球C、Vの内接球Dを考える。
Kの外側かつCの内部である領域の体積(すなわち、8つの閉領域の和集合の体積)をVとおくとき、Dの体積とVの大小を比較せよ。
慶應義塾大学の大学院生が発見、世界でたった一組の三角形
https://univ-journal.jp/22743/?show_more=1 これまで知られていなかった定理の証明に成功
辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には、
周の長さも面積も共に等しい組が(相似を除いて)たった1組しかない。
これまで知られていなかった定理の証明に成功した。
「同じ長さの針金が二本ある。
一本の針金を、2箇所の有理点で切り(※)、三角形状に並べたら直角三角形になった。
もう一本の針金を、別の2箇所の有理点で切り、三角形状に並べたら二等辺三角形になった。
偶然にもこの二つの三角形の面積が等しくなった。
さて、この二本の針金、どのような長さに切ったか?」
初見では「そんなもの、いくらでもあるだろう」「確定できるの?」等と思うと思うが、
実は、ユニークな答えが存在する立派な問題だった、ようだ。この点は面白い。
※:針金全体の長さを1としたとき、切り分けた針金の長さが有理数になるような切り方。
アンドリュー・ワイルズ フェルマーの最終定理を証明
グリゴリー・ペレルマン ポアンカレ予想を解明
望月新一 ABC予想を証明
ヴォルフガング・ハーケン 四色問題を証明
>>514 奇数のときは外出の答えでいいみたい。
偶数のときがムズい。
うん、やっぱり無理。
>>514は出来たら論文級やね。一抜けた。
>>542 377+352+135=864
366×2+132=864
前
>>534こちらは解答待ちです。
(1/2)(352×135)=23760
66×√(366^2-66^2)=23760
たまたま一つみつけたんじゃないの? ほかにないことをどうやって示したの?
>>514 俺はコンピュータアルゴリズムが専門なんだけど、操作1だけで考えるとソートアルゴリズムなんで、
x,y,z
x,z,y
z,x,y
z,y,x
の試行を操作2で置き換えると考えてみたらうまくいきそう。
>>522 と思ったんだけど結構ムズいよ。
操作1だけで全ひっくり返しを最低何回で表示できるか?っていうのはCoxeter Groupのlongest elementのreduced expressionを求める問題として古くからもあり、結果もでてる。
結果は1~nの文字を操作1だけで全ひっくり返す必要回数はn(n-1)/2。
操作2は操作1を3回で表示できるから最低でも┌n(n-1)/6┐は必要だとわかる。(┌ ┐はceiling、切り上げ関数。)
この回数での解が見つかれば終わりで、nが小さいときにはそういう解があるんだけどnが大きくなるとトタンに無理。
となると必要回数の評価はCoxeter Groupの理論が使えない。
それで操作2も含めてCoxeter Systemの中に組み入れられないかとも思ったけど残念ながら操作2を含めるとCoxeter Systemにならない。
で、既存の理論使うのは無理。
となると必要最低回数(=下からの評価)が激ムズになる。
結局のところ「おお、こんな回数でできるんや。きっとこれが最小回数。でも証明できんなぁ。」まではいっても、そこまでの尻切れトンボで終わる可能性しか見えない。
数学やってるとそういうのイヤなんだよねぇ。前にあった8面体の話と同じ運命を辿るっぽい。
奇数偶数の話もあったけど、
1,3,5,7,9
2,4,6,8,10
というふうに分ければ操作2は操作1になる。どうにかならんか?
abcd
1342
1324
1423
1432
4132
4231
4123
2314
2413
2341
2431
3142
3241
3214
3124
これに一つ足りないabcdの組み合わせは何ですか?
>>554 そう、それが最初に考えたことでたとえばn=9のとき13579と2468それぞれにわけて考えて
(13)(35)(57)(79)(57)(35)(13) (35)(57)(35)
(24)(46)(68)(46)(24) (46)
はそれぞれ13579と2468の総ひっくり返しのreduced expressionになってる。
実際 5・4/2 + 4・3/2 = 16 で置換群の Longest Element の公式とピッタリ。
しかし、問題はそこじゃない。
これがホントにこれ以上短い表現を持たないかどうか。
一般論が教えてくれるのは奇数は奇数、偶数は偶数で一個飛ばしの交換しか使わない場合にはこれが最短というだけ。
隣接する交換を使ったらもっと短くなる可能性を否定できない。
ただ、多分これが最短の表示だとは思う。
証明に一般論使えないだけで。
奇数のときはこれでなんとかなるかもしれないけど、偶数の場合はなぁんも思いつかん。
>>556 さっき確かめたらa[6]で操作1を使った最短パターンが出ててたわ。
操作2だけじゃ最短にならない。
>>557 偶数のときは必然的に最低でもn/2回の操作1が必要であることはわかる。
なぜなら偶数のときは1→n、2→n-1…と奇偶を変えないといけないから。
操作2は奇偶を変えないので操作1は絶対必要。
操作1一回につき奇偶を変えられるのは2つなので最低n/2回の操作1が必要なのはわかる。
で、話が(12)(34)(56)…(n-1 n)やったあとに、あとは操作2だけでなんとかなるならまだいいんだけどn=4、6ぐらいで確かめると、そうはいかない事がわかるのでもうお手上げ。
勘でゴチャゴチャやれば “多分これじゃね?” ってのが出てくるかもくらいが関の山。
それが最簡表示であることを証明できる気はとてもしない。
nが奇数で操作2だけでなんとかなる場合ならできるかもしれないけど。
少なくとも掲示板で暇つぶしに解くレベルの問題じゃない希ガス。
もしたった一つに決まるなら、
a^2=b^2+c^2
bc/2=(d/2)√{e^2-(d/2)^2}
a+b+c=d+2e
この3式で未知数5つ。あとa~eが2以上の自然数ってことぐらい。一つに決まるには条件が足りなくない?
前
>>551逆に条件が足りてるなら方程式で解いてくれよ。
>>559
直角⊿の直辺を a, b とし、二等辺△を二等分した直角⊿の斜辺をc, 底辺をd' とする。
周長: a+b + √(aa+bb) = 2c + 2d'
面積: (1/2)ab = d'√(cc-d'd') (c>d')
となる。 >>443
ピタゴラス数を
a = kk-LL,
b = 2kL,
c = 6(mm+nn),
d' = 6(mm-nn),
とおけば、
周長/2: k(k+L) = 12mm, …… (1)
面積: kL(kk-LL) = 6(mm-nn)・12mn
辺々割って
L(k-L) = 6(mm-nn)n/m, …… (2)
これらを満たす正の整数の組は (k, L, m, n) = (16, 11, 6, 5) しかないという…
>>447 前
>>559 a^2=b^2+c^2
bc/2=(d/2)√{e^2-(d/2)^2}
a+b+c=d+2e
>>560わかりました。ここから16、11、6、5という数字を導きたいと思います。
いずれも吉数ですね。しかもかなりの大吉数。
a^2=b^2+c^2
bc/2=(d/2)√{e^2-(d/2)^2}
√(b^2+c^2)+b+c=d+2e
つづく……。
>>536 の
「○と┏」 の話は 逆順化の操作とどのように対応しているのでしょうか。
アイデアというか概略を教えて下さい
半径が等しい2つの円CとDを、CとDの交点がちょうど2つとなるように空間に配置する。
このとき各円は、その交点を境に短い弧と長い弧に分かれる(分かれた弧の長さが等しい場合、どちらを短い弧としてもよい)。
短い弧同士、長い弧同士の長さはそれぞれ等しいことを証明せよ。
>>563 グラフ書いて交点を結ぶ直線を中心に対称というのじゃだめ?
C(もしくはD)を、交点を結ぶ直線まわりに回転させて同一平面にのせないとダメでね
>>565 じゃあ、回転移動で重ねればいいってことか。
>>444の記事の論文ってどこに掲載されるの?もう手に入る?だれか手に入れた?
>>540 > >n=2k+1のとき a[n]=k^2、n=2kのとき a[n]=k^2 - 2[(2k-1)/5]
> になるのは何故ですか?
すまん。特定の敷き詰め方で考えていたので、間違ってますね。
n=2k+1のとき、操作2だけでk^2回でできるけど、操作1も使うと回数を減らせるのかが、関心事。
n=15のとき、「○と┏」では43回でできる予想になるけど、どうなのか。
>>562 隣接互換での逆順化(reduced word)は階段状のタブローの標準版あるいはbalanced tableauに対応するので、
階段状のタブローで考えて、nが9以下で数が合ったので、それっぽいかなと思っただけです。
いろいろ試して、「○と┏」から単純に作った標準版からは直接問題の逆順化には対応しないことが分かったので、予想は間違ってそう。
参考論文
Balanced tableaux
https://www.sciencedirect.com/science/article/pii/0001870887900636 >>563 n=15のとき43個の◯と┌での敷き詰めがあるという事?
どんな敷き詰めですか?
>>569 ┏━○┏━○┏━○┏━○┏━
┃┏━┃┏━┃┏━┃┏━┃
○┃┏━┃┏━┃┏━┃○
┏━┃┏━┃┏━┃┏━
┃┏━┃┏━┃┏━┃
○┃┏━┃┏━┃○
┏━┃┏━┃┏━
┃┏━┃┏━┃
○┃┏━┃○
┏━┃┏━
┃┏━┃
○┃○
┏━
┃
塊のまんまで┌を移動させる規則を作ればできそうな気もしてきた。
>>570 thx
┌─
│◯
は
│├┤│
├┤├┤
│├┤│
を操作2回
├┼┤│
│├┼┤
で実現できるので大丈夫だけど
┌─
│┌─
│◯
は
│├┤├┤│
├┤├┤├┤
│├┤├┤│
を操作3回で実現できるという意味だと思いますができます?
>>447 >>560
ピタゴラス数を
a = i(kk-LL),
b = i(2kL),
c = j(mm+nn),
d' = j(mm-nn),
とおけば、
ik(k+L) = 2jmm, …… (1)
iL(k-L) = j(mm-nn)n/m, …… (2)
gcd(i, j) = 1, …… (3)
これらを満たす正の整数の組は (i, j, k, L, m, n) = (1, 6, 16, 11, 6, 5) しかない… 半径が等しい2つの円CとDを、CとDの交点がちょうど3つとなるように空間に配置する。
無理だろうな。
ジョーカーを除いたトランプ52枚の中から1枚の
カードを抜き出し、表を見ないで箱の中にしまった
そして、残りのカードをよく切ってから
3枚抜き出したところ、3枚ともダイヤであった
このとき、箱の中のカードがダイヤである確率はいくらか
前
>>574 1/4
∵52枚のカードから1枚引くとき、52枚のうち13枚はダイヤだったから
前
>>576訂正。前の前
>>561 >>574 1/4
∵52枚のカードから1枚引くとき、52枚のうち13枚はダイヤだったから
前
>>577 そのダイヤがどんなダイヤだろうと関係ない。ましてや有名か否かなど。
52枚のうち13枚はダイヤ。それがトランプのルール。
引いたあと箱の中のカードが影響を受けるならそれはマジック。
>>579 ジョーカーを除いたトランプ52枚の中から1枚の
カードを抜き出し、表を見ないで箱の中にしまった
そして、残りのカードをよく切ってから
13枚抜き出したところ、13枚ともダイヤであった
このとき、箱の中のカードがダイヤである確率はいくらか
>>579 最初に1枚を引いた時点では1/4だけど、その後残りのカードの情報を知ったら可能性は絞られるんじゃない
箱の中のカードは影響を受けない
が、確率は観測の影響を受ける
>>571 考えている対応関係は
>>568の論文のFig.5.2のようなもので、○と┏の位置が直接あみだくじの横棒の位置に対応していません。
例えば下のものに数を入れて標準盤もどきにして
┏━○
┃○
○
114
13
2
114④
13③
2②
①
↓
11□③
13④
2②
①
↓
□11③
□1②
2④
①
↓
□11③
□1②
□①
④
↓
□□□①
□□②
□③
④
というような感じで
①②③④
├┼┤│
││├┤
│├┤│
├┤││
④③②①
に対応しないかなあ、と考えています。
単純に場合分けすればいい。
場合分けの確率も考慮して。
>>536 とりあえず
>n=2kのとき a[n]=k^2 - 2[(2k-1)/5]。
だとa[10] = 23になるけどn=10で21回の解があった。
import Data.Ratio
import Data.List
exchange (i, j) x = let
(a,b) = (min i j,max i j)
in
(take (a-1) x) ++ [x!!(b-1)] ++ (drop a $ take (b-1) x) ++ [x!!(a-1)] ++ (drop b x)
apply exs ns = foldr exchange ns exs
exs3 = [(5,7),(3,5),(5,6),(6,8),(4,6),(6,7),(7,9),(5,7),(2,3),(3,5),(5,7),(7,9),(1,3),(3,4),(4,6),(6,8),(8,10),(6,8),(4,6),(2,4),(1,2)] :: [(Int,Int)]
main = do
print $ apply exs3 [1..10]
print $ length exs3
―実行結果―
[10,9,8,7,6,5,4,3,2,1]
21
>>574 >>581と同じ結果になった。
高1で習うただの条件付き確率
(あと、ノイズの相手をして増幅するのはやめてほしい>各位)
kを正の整数の定数として
山札からダイヤがn枚抜き出された時の
n=3の時にq=10/49になる関数を発見しました
5≦k≦15の範囲において以下の式が成り立つ
ダイヤである確率は
∵q=1-{{165n-(k-4)n^2+351}/(208n-kn^2+468)}
k=7,n=3の時q=10/49
k=7,0≦n≦13の範囲において
1/4
52/223
187/856
10/49
25/132
232/1333
77/488
74/527
205/1684
20/197
7/88
106/1909
19/652
0
いや、普通に
事象A:箱の中のカードがダイヤ
事象B:残りから3枚引いたら全てダイヤ
P(B)
=(1/4)*(12/51)*(11/50)*(10/49)+(3/4)*(13/51)*(12/50)*(11/49)
=1320/(4*49*50*51)+5148/(4*49*50*51)
=6468/(4*49*50*51)
P_B(A)
=P(A∧B)/P(B)
={(1/4)*(12/51)*(11/50)*(10/49)}/{6468/(4*49*50*51)}
=1320/6468
=10/49
んにゃぴ…
>>586 すばらしい。よく見つけましたね。
次の21個の敷き詰め方があるので、予想の反例とはならないですね。
┏━○┏━○┏━○
┃┏━┃┏━┃○
○┃┏━┃┏━
┏━┃┏━┃
┃┏━┃○
○┃┏━
┏━┃
┃○
○
>n=2kのとき a[n]=k^2 - 2[(2k-1)/5]。
>>568で言ったように、その式は間違いでした。
n=16まで描いてみたところ、次のようになりそうです:
a[1]=0, a[2]=1, a[3]=1, a[4]=4, a[5]=4, a[6]=7, a[7]=9,
n≧8のとき、a[n] = n(n+3)/6 + 2 (n≡0 mod 3), (n-1)(n+4)/6 (n≡1,2 mod 3)
D:ダイヤの枚数、H:それ以外のスートの枚数
抜き取ったn枚が全部ダイヤのとき
T=D+Hとして
求める確率pは ( choose(n,r)は組み合わせnCr = n!/((n-r)!*r!)
p=(D/T * choose(D-1,n)/choose(T-1,n)) /((D/T * choose(D-1,n)/choose(T-1,n)) + H/T * choose(D,n)/choose(T-1,n))
展開して整理すると
=(D-n)/(D+H-n)
D=13 H=39 n=3 なら p= 10/49
>>586,590
n=10で19回(最小)のものが見つかりました。(予想では21回が最小)
よって、
>>536の予想は非成立です。残念。
a[10]=19 です。
[(1,3),(2,4),(3,5),(1,3),(5,7),(4,5),(7,9),(5,7),(3,5),(2,3),(9,10),(7,9),(5,7),(3,5),(1,3),(7,8),(5,7),(3,5),(5,6)]
>>592 a[10] ≧ 19 は証明済みですか?
あとその shape は19個以下の◯と┌でタイリング出来ないことも証明済みですか?
>>580わかった。13枚ダイヤが出たら箱の中にダイヤがある確率は0。ダイヤ3枚はあとの人のために引かなかったことになる。>>574つまり分母が52-3で、分子が13-3。10/49
_∥∩∩]∥◇|∩∩_∥
∩((-。-)。∥>/( (`。)∩
(^)(っ[ ̄]∥/(υυ(
 ̄)「 ̄ ̄]∥_υυ/( ̄
)_)□/UU[∩∩_/∩∩(_
~~ ~/_/(__)(^)_)~ ~ ~~~ ~~~ ~~~ ~~~ ~~~~ ~~~ ~~~ ~ ~ ~ ~ 前>>579 平方数のフィボナッチ数は144しかないことを証明せよ。
>>595 フィボナッチ数列を漸化式、
an+1=an-1+an
a1=a2=1
(n≧2、Zэn nは2以上の整数)とおくと、
a1=1=1^2
a12=144=12^2
この漸化式のグラフをxy平面に描くと、
y=x^2のグラフは、
(x,y)=(1,1)で漸化式のグラフと一致し、xが増加するにしたがってずっとyの値が上にあり、(x,y)=(12,144)でふたたび一致。以降はxがいくら増加しようとも永遠にyの値が下にあるグラフを描く。
1=1^2であるが、n≧2の整数であるから考えなくてよい。
∴ 12^2=144のみが題意を満たす
赤玉、青玉、白玉がk個ずつある。
これら3k個の玉を数珠状に並べるとき、
「どの連続した3個の玉の並びについても、赤玉、青玉、白玉が全て含まれることはない」
ような並べ方の総数をkで表せ。
>>597 回転、反転で一致するのは同一視するの?
>>595 α=(1-√5)/2、β=(1+√5)/2とし、Fn = (β^n-α^n)/(β-α)、Ln = β^n+α^n)とおく。
帰納法により
Lnは9の倍数⇔n ≡ 6 (mod 12)。
nが3の倍数でない偶数→Ln ≡ 3 (mod 4)。
また
Fm + Fn = FuLv (u = (m+n)/2、v=(m-n)/2)
であるから m-n = 2ik のとき
Fm ≡ (-1)^iFn (mod Lk)
である。
nを±1,2,12でない自然数とする。
m = {±1,2,12}をn ≡ m(mod 4)とし、n-m = 2ik (kは2以上の2のべき、i:奇数)とする。
このとき
Fn ≡ (-1)^iFm (mod Lk)
で、Lk ≡ 3 (mod 4)、Fmは平方数であるからFnは平方数でない。
以上によりフィボナッチ数列に現れる平方数は1と144のみである。
どうでもいいがF_n=n^2になってるんだね 他の自然数の2乗でもいいのに
>>600 訂正
n-m = 2ik (kは2以上の2のべき、i:奇数)とする。
kが4以上またはm≠12ならLkは3で割り切れないので
>>400のままでよい。
kが2、m=12のとき。
n=12+4k (k:奇数)だからnは8の倍数。
l=n/2として
Fn = FlLl、(Fl,Ll)=1,2
よりFまたはFl/2のいずれかが平方数。
くりかえしてn=ki(kは2べき、iは奇数)とおくとき
Fi,Liがともに平方数、または2Fi,2Liがともに平方数。
Fiが平方数になる奇数 i は
>>600よりi = 1。
しかしこのときL1=2は平方数でない。
2Fiが平方数となる奇数iは
>>600と同様にしてi=±3。
i>0よりi=3であるがこのとき2L3=8は平方数でない。
t+1/t=10 のとき t-1/t の取りうる値は?
>>603 ±√((t+1/t)^2-4)=±√96 = ±4√3
次の命題の真偽を述べ、それを証明せよ。
「ある正n角形をSnを考える。Snの上にすべての頂点が乗る正k角形の全てからなる集合をA(k)とおくと、A(k)が無限集合になるkはk=nのみである。」
>>596 何の証明にもなってないだろw
そもそもFn=n^2を証明しろなんて問題じゃないから
これドヤ顔で回答するやつがコテ付けてこのスレに45レスもしてるのがやばいよ
途中送信した
条件は「Fn=n^2を満たすnを探せ」ではなく「Fn=m^2を満たすnmの組を探せ」だってことね
イナ ◆/7jUdUKiSM=稲次将人
プロフィール見ると東大出身らしいが
よく
>>596みたいなクソ証明もどき載せられるような奴が東大入れたな
>>606 偽
(凡例)
nが合成数で、kがその約数 (k≠1, k≠n) のとき。
Snの周をk等分するk点がなすk角形は、中心の周りにk回対称なので、正k角形となる。
したがって A(k) に含まれる。
∴ A(k) は無限集合
>>606 S6上にすべての頂点がのる正三角形は無限にあるので偽。
>>609 出身???ということは大学出てるん????
>>600 m-n = 2ik のとき
Fm ≡ (-1)^iFn (mod Lk)
ここの証明ができてない
G:有限群 φ:Gの自己同型
・ ∀x∈G について φ(φ(x))=x
・ φ(x)=x をみたすxは単位元のみ
このときGは可換であることを示せ
>>615 F[x] + F[y] = F[(x+y)/2]L[(x-y)/2]
により
F[y+2z] + F[y] ≡ 0 (mod L[z])
F[y+2z] ≡ (-1)F[y] (mod L[z])
これを繰り返し用いて
F[y+2iz] ≡ (-1)^i F[y] (mod L[z])。
>>617 > a(n) = ceiling(n(n+1)/6) for n > 5
おお、これが作れるなら最小性の証明できる。
なら話は違うな。
存在証明か…
>>597 K=3のときの並びをコンピュータで算出してみました。
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 赤 白 赤 白 白 青 青 赤 青
[2,] 赤 白 赤 白 白 青 青 青 赤
[3,] 赤 白 赤 赤 白 白 青 青 青
[4,] 赤 白 白 青 白 青 青 赤 赤
[5,] 赤 白 白 白 青 青 赤 赤 青
[6,] 赤 白 白 白 青 青 赤 青 赤
[7,] 赤 白 白 白 青 青 青 赤 赤
[8,] 赤 白 白 白 赤 赤 青 青 青
[9,] 白 赤 赤 赤 青 青 白 白 青
[10,] 白 赤 赤 赤 白 白 青 青 青
[11,] 白 赤 白 赤 赤 青 青 白 青
[12,] 白 赤 白 白 赤 赤 青 青 青
[13,] 青 赤 赤 赤 白 白 青 青 白
[14,] 青 赤 赤 赤 青 青 白 白 白
[15,] 青 赤 青 赤 赤 白 白 青 白
[16,] 青 赤 青 青 赤 赤 白 白 白
>>613 いや、オッサンになって数学全く使わない仕事してんならこんなもんだろう。頑張ってる方
>>620 あ、いやちがう。
>>617のa[n]は
>Maximal number of points that can be placed on a triangular grid of side n so that there is no pair of adjacent points.
だ。
そのような点の配置から現問題の条件をみたす standard tableaux が作れるかどうかはわからない。
>>614おもに高校生のときに数学をやってたんだからあながち高校生で間違ってない。前
>>596いや高校生にちがいない。
>>593 > a[10] ≧ 19 は証明済みですか?
PCで最小操作数(最短経路)をダイクストラ法で探索した結果です。
> あとその shape は19個以下の◯と┌でタイリング出来ないことも証明済みですか?
これもPCで探索した結果21が最小でした。
また
>>617の参考文献で証明されていそうです。
>>617 ありがとう。
>>590の訂正した式でよさそうです。
(ときたまOEISを使うのに、使うことを思いつかなかったとは…)
n=11で23回(最小)のものが見つかりました。(すでに間違いだと判明した)予想だと25回です。
操作2だけでは25回になるものでしたが、操作1を混ぜることで小さくなります。
すこし不思議に感じるかもしれませんが、これは操作2が常に転倒数を3だけ変化させるわけではなく、
1だけ変化させることもあることによります。
転倒数の変化を追うことで問題解決のヒントが得られるかもしれません。
(23,[(1,3),(2,4),(3,5),(1,3),(4,6),(6,8),(4,6),(8,10),(7,8),(5,7),(3,5),(2,3),(7,9),(5,7),(3,5),(1,3),(9,11),(7,9),(5,7),(3,5),(1,3),(7,8),(5,7)])
>>625 >PCで最小操作数(最短経路)をダイクストラ法で探索した結果です。
そうなんですか。
じゃあやっぱりこの問題手がかりなしですね。a[n] = ┌n(n-1)/6┐なら最小性が必然になりますが、
┌10・9/6┐=15 ≠ 19 = a[10]
なのであれば下からの評価はほとんど出来る気がしない。
まあ
>>617のサイトみたく
n≧✕✕ ⇒ a[n] = ┌n(n-1)/6┐
となってる淡い期待もありますが。
望み薄ですねぇ。
>>626 嘘書いた。
nが偶数のときは一般論+αから一瞬ででてくる下から評価は
a[n] ≧ ┌ n(n-2)/6 ┐+ n/2
であってn=10のときは
┌80/6┐+10/2 = 18
だからもしかしたら、もうちょい議論すれば正しい下から評価でても不思議はないか。
>>618 x≠e である x∈G が φ(x) を対をなすので、#Gは奇数。
Feit-Thompson の定理より、Gは可解群。
次の補題に帰着した。
〔補題〕
位数が奇数の可解群はつねに可換群か?
>>597 環状に並べるとする。 ローテーションしてもよい。
・k=1 のとき
なし。
・k=2 のとき
AABBCC → ABBCCA →,
2 x 6 = 12
・k=3 のとき
AAABBBCCC → AABBBCCCA → ABBBCCCAA [7] →,
AAABBCBCC → AABBCBCCA → ABBCBCCAA [4] → AABABBCCC → ABABBCCCA [2] → ABAACCCBB → ABBCCCAAB → AABBBCCAC → ABBBCCACA [6] →,
12 x 6 = 72
>>628
有限群Gの位数が奇数 ⇒ Gの部分群の位数も奇数。 … ラグランジュの定理(群論)
奇数位数の単純群が巡回群だけなら、「位数が奇数の有限群は可換群」と言いたい所。
これが端緒になって有限単純群の分類研究が始まったのかも知れない。 >>597はどうみても出題ミスやろ?
こんなん解けんやろ?
まぁ900くらいになったらみんな答え上げてくるけど
>>597は答え上がらんと思う。
>>618 とりあえず自分も分かったことを書いてみる。
・主張が正しいとすれば、φは逆元をとる写像である。
G が可換であるとする。
任意の G の元 x に対して、
φ(xφ(x)) = φ(x)x = xφ(x)
であるから、φの条件より xφ(x)=e (e は単位元)。
したがって φ(x)=x^(-1)
・無限群だと反例がある。
G を 2 元生成自由群とする。生成元を a,b とする。
自己同型 φ:G→G を φ(a)=b, φ(b)=a によって定まるものとすれば、
φは条件を満たすが、G は非可換である。
>>632 逆に、φが自己同型かつ逆元をとる写像なら、逆元をとる操作を「~」として
xy = φ((xy)~) = φ(y~ x~) = φ(y~) φ(x~) = yx
から可換であることが分かる。
つまり、φが逆元をとる写像であることを位数の有限性を利用して示せばいいわけか。
>>597 k=4のときをPCで列挙してみた。回転および鏡像で同じになるものは1通りと数える。
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
[1,] 赤 赤 赤 赤 白 白 白 白 青 青 青 青
[2,] 赤 赤 赤 赤 白 白 白 青 白 青 青 青
[3,] 赤 赤 赤 赤 白 白 白 青 青 白 青 青
[4,] 赤 赤 赤 赤 白 白 青 白 白 青 青 青
[5,] 赤 赤 赤 赤 白 白 青 白 青 白 青 青
[6,] 赤 赤 赤 赤 白 白 青 青 白 白 青 青
[7,] 赤 赤 赤 赤 白 白 青 青 青 青 白 白
[8,] 赤 赤 赤 赤 青 青 白 白 白 白 青 青
[9,] 赤 赤 赤 白 赤 白 白 白 青 青 青 青
[10,] 赤 赤 赤 白 赤 白 白 青 白 青 青 青
(中略)
[174,] 青 赤 青 青 赤 赤 赤 白 白 青 白 白
[175,] 青 赤 青 青 赤 赤 白 赤 白 白 青 白
[176,] 青 赤 青 青 赤 青 赤 赤 白 白 白 白
[177,] 青 赤 青 青 青 赤 赤 赤 白 白 白 白
[178,] 青 赤 青 青 青 赤 赤 白 赤 白 白 白
[179,] 青 赤 青 青 青 赤 赤 白 白 赤 白 白
[180,] 青 赤 青 青 青 白 白 赤 赤 赤 白 白
180通り
>>634 K=2のときは回転・反転を同一視すると
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 赤 白 白 青 青 赤
の一通り
>>635 回転・反転を考えなければ
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 赤 白 白 青 青 赤
[2,] 赤 青 青 白 白 赤
[3,] 赤 赤 白 白 青 青
[4,] 赤 赤 青 青 白 白
[5,] 白 赤 赤 青 青 白
[6,] 白 青 青 赤 赤 白
[7,] 白 白 赤 赤 青 青
[8,] 白 白 青 青 赤 赤
[9,] 青 赤 赤 白 白 青
[10,] 青 白 白 赤 赤 青
[11,] 青 青 赤 赤 白 白
[12,] 青 青 白 白 赤 赤
の12通り
k=5だと
並べ方は順列で15!/(5!5!5!)=756756通りのうち
3個連続に3色含まないのは13194通りまでは出せた。
回転・鏡像を同一視しての計算はR言語では計算が終わりそうにない。
>>621 先頭と最後を繋げると3色揃うから間違っているな。
やり直そう。
>>621 k=3で
> print(matrix(c("赤","白","青")[core],ncol=3*k),quote=F)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 赤 白 赤 白 白 青 青 青 赤
[2,] 赤 白 白 青 白 青 青 赤 赤
[3,] 赤 白 白 白 青 青 赤 青 赤
[4,] 赤 白 白 白 青 青 青 赤 赤
の4通り
>>634 k=4で
> print(matrix(c("赤","白","青")[core],ncol=3*k),quote=F)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
[1,] 赤 赤 赤 赤 白 白 白 白 青 青 青 青
[2,] 赤 赤 赤 赤 白 白 白 青 白 青 青 青
[3,] 赤 赤 赤 赤 白 白 白 青 青 白 青 青
[4,] 赤 赤 赤 赤 白 白 青 白 白 青 青 青
[5,] 赤 赤 赤 赤 白 白 青 白 青 白 青 青
[6,] 赤 赤 赤 赤 白 白 青 青 白 白 青 青
[7,] 赤 赤 赤 赤 白 白 青 青 青 青 白 白
[8,] 赤 赤 赤 赤 青 青 白 白 白 白 青 青
[9,] 赤 赤 赤 白 赤 白 白 白 青 青 青 青
[10,] 赤 赤 赤 白 赤 白 白 青 白 青 青 青
[11,] 赤 赤 赤 白 赤 白 白 青 青 白 青 青
[12,] 赤 赤 赤 白 白 赤 白 白 青 青 青 青
[13,] 赤 赤 赤 白 白 白 白 青 青 赤 青 青
[14,] 赤 赤 赤 白 白 白 白 青 青 青 赤 青
[15,] 赤 赤 赤 白 白 白 青 白 青 青 赤 青
[16,] 赤 赤 赤 白 白 青 白 白 青 青 赤 青
[17,] 赤 赤 赤 白 白 青 青 赤 青 青 白 白
[18,] 赤 赤 赤 青 青 白 白 赤 白 白 青 青
[19,] 赤 赤 白 赤 赤 白 白 白 青 青 青 青
[20,] 赤 赤 白 赤 赤 白 白 青 白 青 青 青
[21,] 赤 赤 白 赤 赤 白 白 青 青 白 青 青
[22,] 赤 赤 白 赤 赤 青 青 白 白 白 青 青
[23,] 赤 赤 白 赤 白 赤 白 白 青 青 青 青
[24,] 赤 赤 白 赤 白 白 白 青 青 赤 青 青
[25,] 赤 赤 白 赤 白 白 白 青 青 青 赤 青
[26,] 赤 赤 白 赤 白 白 青 白 青 青 赤 青
[27,] 赤 赤 白 白 赤 赤 白 白 青 青 青 青
[28,] 赤 赤 白 白 赤 赤 青 青 白 白 青 青
[29,] 赤 赤 白 白 赤 白 白 青 青 赤 青 青
[30,] 赤 赤 白 白 赤 白 白 青 青 青 赤 青
[31,] 赤 赤 白 白 白 赤 赤 青 青 白 青 青
[32,] 赤 赤 白 白 白 白 赤 赤 青 青 青 青
[33,] 赤 赤 白 白 白 白 青 青 赤 赤 青 青
[34,] 赤 赤 白 白 白 白 青 青 赤 青 赤 青
[35,] 赤 赤 白 白 白 白 青 青 青 赤 赤 青
[36,] 赤 赤 白 白 白 青 白 青 青 赤 赤 青
[37,] 赤 赤 白 白 青 白 白 赤 赤 青 青 青
[38,] 赤 赤 白 白 青 白 白 青 青 赤 赤 青
[39,] 赤 赤 白 白 青 青 赤 赤 白 白 青 青
[40,] 赤 赤 白 白 青 青 赤 赤 青 青 白 白
[41,] 赤 赤 白 白 青 青 白 白 赤 赤 青 青
[42,] 赤 赤 白 白 青 青 青 白 白 赤 赤 青
42通り
>>637 修正
k=5だと
並べ方は順列で15!/(5!5!5!)=756756通りのうち
3個連続に3色含まないのは10050通りまでは出せた
>>618 これは使えるだろうか…
次の場合に示せれば十分である。
「ある元 x∈G が存在して、G は x,φ(x) で生成される。」 …(*)
∵
任意に x∈G をとる。
>>633より、φ(x)=x^(-1) を示せばよい。
x,φ(x) で生成される部分群を H とおく。
φ(H)⊂H が成り立つ。
H が有限群であることとφの単射性から、φ は H の自己同型を誘導する。
φ の H への制限を φ_H とおく。
H と φ_H は問題の条件および (*) を満たす。
もし H において
>>618が成り立てば、
>>632より φ(x)=x^(-1) である。□
>>640 >>641
k=4 のとき
[ 1] AAAABBBBCCCC → 4
[ 8] AAAACCBBBBCC → [32] AABBBBAACCCC → [ 7] AAAABBCCCCBB → 6
[ 2] AAAABBBCBCCC → [14] AAABBBBCCCAC → [ 9] AAABABBBCCCC → 12
[ 3] AAAABBBCCBCC → [35] AABBBBCCCAAC → [12] AAABBABBCCCC → 12
[ 4] AAAABBCBBCCC → [13] AAABBBBCCACC → [19] AABAABBBCCCC → 12
[ 5] AAAABBCBCBCC → [34] AABBBBCCACAC → [23] AABABABBCCCC → 12
[ 6] AAAABBCCBBCC → [33] AABBBBCCAACC → [27] AABBAABBCCCC → 12
[10] AAABABBCBCCC → [15] AAABBBCBCCAC → [25] AABABBBCCCAC → 12
[11] AAABABBCCBCC → [36] AABBBCBCCAAC → [30] AABBABBCCCAC → 12
[16] AAABBCBBCCAC → [24] AABABBBCCACC → [20] AABAABBCBCCC → 12
[17] AAABBCCACCBB → [31] AABBBAACCBCC → [22] AABAACCBBBCC → [37] AABBCBBAACCC → [42] AABBCCCBBAAC → 12
[39] AABBCCAABBCC → ABBCCAABBCCA → 2
[40] AABBCCAACCBB → [28] AABBAACCBBCC → [41] AABBCCBBAACC → 6
[29] AABBABBCCACC → [21] AABAABBCCBCC → [38] AABBCBBCCAAC → 12
[26] AABABBCBCCAC → 4 >>628 >>630 φはGの自己同型である。
e以外の元x∈Gを2個1組の対 {x,φ(x)} に分けたもの。
逆元でなくてもいいと思うけど・・・・
>>597 朝になったらk=5の計算が終わってた。
> print(matrix(c("赤","白","青")[core],ncol=3*k),quote=F)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15]
[1,] 赤 赤 赤 赤 赤 白 白 白 白 白 青 青 青 青 青
[2,] 赤 赤 赤 赤 赤 白 白 白 白 青 白 青 青 青 青
[3,] 赤 赤 赤 赤 赤 白 白 白 白 青 青 白 青 青 青
[4,] 赤 赤 赤 赤 赤 白 白 白 白 青 青 青 白 青 青
[5,] 赤 赤 赤 赤 赤 白 白 白 青 白 白 青 青 青 青
中略
[331,] 赤 赤 白 白 青 白 白 白 青 青 赤 青 赤 赤 青
[332,] 赤 赤 白 白 青 白 青 白 白 赤 赤 青 赤 青 青
[333,] 赤 赤 白 白 青 白 青 青 白 白 赤 赤 青 赤 青
[334,] 赤 赤 青 赤 赤 青 青 白 白 赤 白 白 白 青 青
[335,] 赤 赤 青 赤 青 青 白 白 赤 白 赤 白 白 青 青
335通りと算出。
全列挙はここにあげた
http://fast-uploader.com/file/7093381709046/ >>618 f:G→Gをf(x)=x^{-1}φ(x)∈Gと定義する。
まず、fは単射であることを示す。f(x)=f(y)ならば、
x^{-1}φ(x)=y^{-1}φ(y)だから、式変形していけば
x^{-1}φ(x)=y^{-1}φ(y)
yx^{-1}φ(x)=φ(y)
yx^{-1}=φ(y)φ(x)^{-1}
yx^{-1}=φ(yx^{-1})
仮定により、yx^{-1}=eでなければならない。よって、y=xとなるので、fは単射である。
Gは有限集合だから、fは全射である。次に、φ(f(x))=f(x)^{-1} (∀x∈G)を示す。
f(x)φ(f(x))=x^{-1}φ(x)φ(x^{-1}φ(x))=x^{-1}φ(x)φ(x)^{-1}x=e
よって、φ(f(x))=f(x)^{-1} (∀x∈G)である。fは全射だから、
φ(y)=y^{-1} (∀y∈G)が成り立つ。よって、x,y∈Gに対して、
φ(xy)=φ(x)φ(y)=x^{-1}y^{-1},
φ(xy)=(xy)^{-1}=y^{-1}x^{-1}
となるので、x^{-1}y^{-1}=y^{-1}x^{-1}である。両辺の ^{-1} を取って
yx=xyとなる。よって、Gは可換である。
>>647 >f(x)φ(f(x))=x^{-1}φ(x)φ(x^{-1}φ(x))
は何故?
>>648 f(x)φ(f(x))の2つのf(x)にf(x)=x^{-1}φ(x)を代入すれば
f(x)φ(f(x))=x^{-1}φ(x)φ(x^{-1}φ(x))
>>597
a_{kk+4} ?
k=0 a_4 = 0,
k=1 a_5 = 0,
k=2 a_8 = 1, >>635
k=3 a_13 = 4, >>639
k=4 a_20 = 42, >>640 >>641
k=5 a_29 = 335, >>646
k=6 a_40 = 3154,
k=7 a_53 = 30196,
http://oeis.org/A206556
(Number of 6's in the last section of the set of partitions of n) >>651 >Number of 6's in the last section of the set of partitions of n)
の意味すらわからんorz。
lambda n: sum(list(p).count(6) for p in Partitions(n) if 1 not in p)
って python? R?
どういう計算してるんですか?
>>653 > って python? R?
Sage(SageMath)
http://www.sagemath.org/ Pythonを使った数式処理ソフト
> lambda n: sum(list(p).count(6) for p in Partitions(n) if 1 not in p)
> どういう計算してるんですか?
Also number of occurrences of 6 in all partitions of n that do not contain 1 as a part.
次の行列式を計算し、因数分解せよ。
determinant{{(b+c)^2, c^2, b^2}, {c^2, (c+a)^2, a^2}, {b^2, a^2, (a+b)^2}}
俺には手計算できないんだけど、できる?
>>651 Rで列挙してみたけど、
k=6にすると
順列候補が17,153,136
csvにしたら600Mバイトを越えて
メモリ不足で読み込めず、この計算は断念。
>>654 6 = 6
8 = 6 + 2
9=6+3
10 = 6 + 4 = 6 + 2 + 2
11 = 6 + 5 = 6 + 3 + 2
12 = 6 + 6 = 6 + 4 + 2 = 6 + 3 + 3 = 6 + 2 + 2 + 2
13 = 7 + 6 = 6 + 5 + 2 = 6 + 4 + 3 = 6 + 3 + 2 + 2
14 = 8 + 6 = 6 + 6 + 2 = 6 + 5 + 3 = 6 + 4 + 4 = 6 + 4 + 2 + 2 = 6 + 3 + 3 + 2 = 6 + 2 + 2 + 2
こういう意味かな?
でもこの意味だと流石に一致する気が全くしないんだけど。
あ、ちがう、a_{k+4}ね。なら可能性あるか……
>>647 お見事
ちなみにf(x)=x^{-1}φ(x)の意味を考えるとしたら
単位元とのズレ、とでもなるのでしょうか
またこのようなf(x)を考えるのはよくあること?
>>618 これは美しい証明を得たが、
それをみると自然に次の問が浮かんでくる
G:有限群 φ:Gの自己同型
・ ∀x∈G について φ^{n}(x)=x
・ φ(x)=x をみたすxは単位元のみ
このときGは可換であるか?
ただし、φ^{1}=φ(x)、 φ^{n}(x)=φ(φ^{n-1}(x)) である。
>>651 自分もPCで
>>597を数えたら、k=6 で 3501、k=7 で 36820 だった。
def three_letter_nonadjacent_words(counter, word, letters="abc"):
if sum(counter) == 0:
yield word
return
for i,x in enumerate(letters):
if counter[i] > 0:
if len(word) < 2 or {x,word[-1],word[-2]} != set(letters):
c = list(counter)
c[i] -= 1
yield from three_letter_nonadjacent_words(tuple(c), word + x)
def circularly_legal(word, letters=set("abc")):
return {word[0],word[-1],word[-2]} != letters \
and {word[1],word[0],word[-1]} != letters
def circular_three_letter_nonajacent_words(k):
for word in three_letter_nonadjacent_words((k,)*3,""):
if not circularly_legal(word):
continue
yield word
def num_fixed_perms(word):
n = len(word)
r = 1
for i in range(1,n):
if word[i:] == word[:-i] and word[:i] == word[-i:]:
r += 1
rev = word[::-1]
if word == rev:
r += 1
for i in range(1,n):
if word[i:] == rev[:-i] and word[:i] == rev[-i:]:
r += 1
return r
def num_circular_three_letter_nonajacent_words(k):
#used Burnside's lemma
return sum(num_fixed_perms(word) for word in \
circular_three_letter_nonajacent_words(k)) // (6*k)
for k in range(1,7):
print(k, num_circular_three_letter_nonajacent_words(k))
やっぱり
>>597は無理やろ?
せいぜい計算機でプログラミングの練習位にしかならんと思う。
私もチャレンジしたところ、同じ結果が得られました。
当初、色の入れ替えも同一視するプログラムを作ってしまっていたため、
その結果があります。それも添えます。
k=8は、重複チェック用のメモリが確保できないとのメッセージが出たため、
実行できませんでした。(色入替同一視版は可能でした)
k=2... 1 (1)
k=3... 4 (2)
k=4... 42 (13)
k=5... 335 (67)
k=6... 3501 (651)
k=7... 36820 (6258)
k=8... ?????? (68747)
>>598 >>605 のせいで難しい…
回転・反転を区別すれば a_{k-1}
ここに tan(x) sinh(x) = Σ[n=0,∞] {a_n/(2n)!} x^{2n},
k=1 a_0 = 0,
k=2 a_1 = 2 パターン >>629 >>636
k=3 a_2 = 12 パターン >>629
k=4 a_3 = 142 パターン >>629
k=5 a_4 = 3192 パターン
k=6 a_5 = 116282 パターン
a_n ~ 2 sinh(π/2) (2n)! (2/π)^(2n+1), (n>>1)
http://oeis.org/A009747
(Exponential generating function = tan(x)sinh(x) ) >>667 >回転・反転を区別すれば a_{k-1}
>ここに tan(x) sinh(x) = Σ[n=0,∞] {a_n/(2n)!} x^{2n},
おお、これだけでも十分素晴らしい!
それで十分だから解答のせてたも!
>>667 ?
回転・反転を区別して、色の入れ替えを同一視するなら次になるけど:
k=1: 0
k=2: 2
k=3: 12
k=4: 142
k=5: 1675
k=6: 20648
k=7: 257740
メモリを動的確保に変えて計算させました
k=8... 407629 (68747)
x^12+y^12+z^12-2*((xy)^6+(xz)^6+(yz)^6)=0
(x^n-y^n)≠√((2*y^n+2*x^n-z^n)*z^n)
(y^n-z^n)≠√((2*y^n+2*z^n-x^n)*x^n)
(x^n-z^n)≠√((2*x^n+2*z^n-y^n)*y^n)
√((2*y^n+2*x^n-z^n)*z^n)+√((2*y^n+2*z^n-x^n)*x^n)+√((2*x^n+2*z^n-y^n)*y^n)≠0
結局
>>667 は間違ってるの?
でもまぁなんかの足しになるかもしれないから
>回転・反転を区別すれば a_{k-1}
>ここに tan(x) sinh(x) = Σ[n=0,∞] {a_n/(2n)!} x^{2n},
を導出した過程をうpして下さりませ。
>>597 自分は
>>665に同意。もしきれいな式があったら、興味を持つが。
以下、PCでの探索まとめ。
回転・反転を区別、色の入れ替えを同一視
k=1: 0
k=2: 2
k=3: 12
k=4: 142
k=5: 1675
k=6: 20648
k=7: 257740
k=8: 3255630
k=9: 41515401
回転・反転を同一視、色を区別
k=1: 0
k=2: 1
k=3: 4
k=4: 42
k=5: 335
k=6: 3501
k=6: 36820
k=8: 407629
k=9: 4612825
回転・反転・色の入れ替えを同一視
k=1: 0
k=2: 1
k=3: 2
k=4: 13
k=5: 67
k=6: 651
k=7: 6258
k=8: 68747
k=9: 770248
有名問題だと思うけど。
すべての辺の長さが自然数の三角形で周の長さが nのもの(合同を同一視する)の個数を a[n]としたときの
a[n]の生成関数、つまり f(x) = Σ[n=0,∞] a[n] x^n となる関数 f(x)を求めよ。
>>674 おっしゃる通りです。 Alcuin数列
f(x) = (x^3)/{(1-x^2)(1-x^3)(1-x^4)}
http://oeis.org/A005044 なお、これは周長が n+6 である不等整数辺⊿の数でもある。(辺長≧2 となる。)
a≦b≦c のとき (a,b,c) ⇔ (a+1,b+2,c+3)
>>675 Pythonです。プログラムは
>>664の改変。
速度は気にせず、楽さとわかりやすさで。
バーンサイドの補題を使うことで並べ方どうしの比較をしないのでメモリーを使わず、
時間さえあればいくらでも求められますが、実際は k=10,11 が時間的限界でしょう。
>>676 難しくないので、導出も書いてくださいな。
>>678 横レス。
導出はできるんだけどなにがどうしてこんな綺麗な形になるのかさっぱりわからんから書く気にならない。
なんかもっと美しい方法がありそうで。
>>678 >>679 >>676 のf(x) は
a[n] は自然数n を n=2p+3q+4r (p≧0, q≧1, r≧0) と分割するやり方である。
Number of partitions of n into parts 2, 3, and 4, with at least one part 3.
- Joerg Arndt, 2013/Feb/03
と同値だが、これをどう出すか…
任意の自然数 n に対して、表面積の等しい n種類の直方体が存在することを示せ。
>>681 稜の長さが {2^r, 2^r, 2^(2n-r)-2^(r-1)} である正方形柱 (r=1,2,…,n)
体積は 2^(2n+r) - 2^(3r-1).
>>679 >>680 とりあえず、奇数の場合と偶数の場合にわけて
f(x) = x^3/((1-x^2)(1-x^4)(1-x^6)) + x^6/((1-x^2)(1-x^4)(1-x^6))
で導くルートは見つけた。
でも
>a[n] は自然数n を n=2p+3q+4r (p≧0, q≧1, r≧0) と分割するやり方である。
これで一発解決できるルートがいかにもありそうだよね?
とりあえず奇偶でわけるルート
An = {(u,v,w) | n/2 - u, n/2-v, n/2-wは自然数、u+v+w = n/2、u≦v≦w}
とおけば a[n] = #An。
n が奇数のとき
Bn = {(p,q,r) | p,q,r は非負整数、p+2q+3r=(n-3)/2}
とおき、対応(u,v,w)→(w-v,v-u,u-1/2)によってAn,Bnは一対一対応するから#An = #Bn。
∴Σ[n:odd]a[n]x^n = x^3/((1-x^2)(1-x^4)(1-x^6))。
n が偶数のとき
Cn = {(p,q,r) | p,q,r は非負整数、p+2q+3r=(n-6)/2}
とおき、対応(u,v,w)→(w-v,v-u,u-1)によってAn,Cnは一対一対応するから#An = #Cn。
∴Σ[n:even]a[n]x^n = x^6/((1-x^2)(1-x^4)(1-x^6))。
∴f(x) = x^3/((1-x^2)(1-x^4)(1-x^6)) + x^6/((1-x^2)(1-x^4)(1-x^6)) = x^3/((1-x^2)(1-x^3)(1-x^4))。
3より大きな正整数nに対し、2^n+1の素因数がどれもn未満であるようなものは存在するか?
>>685 これムズい。
ヒントおながいします。
結論は存在する?しない?
>>686 すまないが存在しないだろうと予想している
コンピュータで計算してもそれらしきものは見つからなかった
>>687 現時点で答えないの?
じゃぁそれ書いといてよ。
普通に考えたら有限個しかしないだろう
nが大きくなれば小さい素因数を大量に持たないといけなくなるがそんなのは非現実的
答え持ってない問題を書いていいかどうかは別にしても、現時点で答えがないなら最低でも
>>514のように文面から答え持ってない事がわかるようにせんと駄目だよ。
>>674,679,680,683
見た目より簡単だよ。生成関数の標準的な演習問題くらい?
想定解答は以下のようなもの:
合同は同一視するので三角形の成立条件を考慮すれば、
辺の長さが自然数の三角形と 0<a≦b≦c<a+b をみたす非負整数の組(a,b,c)は一対一に対応することがわかる。
a=s+1, b=a+t, c=b+u とおき、 c<a+b ⇔ c-b<a ⇔ u≦s より s=u+v とおくことにより、
関係式 a=u+v+1, b=u+v+t+1, c=2u+v+t+1 で
0<a≦b≦c<a+b をみたす非負整数の組(a,b,c)と任意の非負整数の組(u,v,t)は一対一に対応することがわかる。
したがって、
f(x) = Σ[n-0,∞] a[n] x^n = Σ[0<a≦b≦c<a+b] x^(a+b+c)
= Σ[u,v,t≧0] x^(4u+3v+2t+3) = (x^3)/(1-x^4)(1-x^3)(1-x^2)。
いや、そのu,v,tが思いつかんかった。
これ
0<a≦b≦c<a+b
からうまくu.v.tを見つけてくるのがミソだと思うけどこれなんか一般論で見つけてくる方法があります?慣れの問題?
>>693 一般論というか基本的技法ですね。
・条件のない非負整数の組と対応させることが目標。
・p<q は p+1≦q とする。
・p≦q をみたす整数の組(p,q)は q=p+k とおくことで k≧0 をみたす整数の組(p,k)と一対一に対応することを使う。
>>692では
0<a から a=s+1 とおき(これで a は 非負整数 s で一対一に表せる)
a≦b≦c から b=a+t, c=b+u とおき(ここまでで 0<a≦b≦c をみたす a,b,c が非負整数 s,t,u で一対一に表せる)
そうすることで c<a+b ⇔ u≦s となるので s=u+v とおく(これで条件をみたす a,b,c が非負整数 v,t,u で一対一に表せた)
となります。
>>680 と
>>692 の関係
(p, q, r) = (t, v+1, u)
>>694 もちろんすべての場合でうまくいくというものではありません。
この場合は運よくうまくいってきれいな形になりましたが。
>>695,680
> a[n] は自然数n を n=2p+3q+4r (p≧0, q≧1, r≧0) と分割するやり方である。
は生成関数の形から分かることで、
三角形とその分割が有用な関係を持つとは思えません。
あったら面白いですが。
>>696,697
なるほど。
本文の場合は
0<a≦b≦c<a+b
⇔0 ≦ (a-1)≦ (b-1) ≦ (c-1) ≦ (a-1)+(b-1)
でa-1,b-1,c-1について整理するとキレイに定数項消えちゃうんだ。
気づかなかったorz。
>>681 稜の長さが { p^(3r), p^(2n+r), p^(2n-r)[p^(2n)-p^(2r)] } である直方体 (r=0,1,…,n-1)
表面積 2p^(6n),
体積 p^(4n+3r)[p^(2n)-p^(2r)],
p>1.
>>682 の拡張
稜の長さが { p^r, p^r, [p^(2n-r)-p^r]/2 } である正方形柱 (r=0,1,…,n-1)
表面積 2p^(2n),
体積 (p^r)[p^(2n)-p^(2r)]/2,
p>1.
■■■■■■■■■■■■■
□□□□□□□□□□□□■
■■■■■■■■■■■□■
■□□□□□□□□□■□■
■□■■■■■■■□■□■
■□■□□□□□■□■□■
■□■□■■■□■□■□■
■□■□■□□□■□■□■
■□■□■■■■■□■□■
■□■□□□□□□□■□■
■□■■■■■■■■■□■
■□□□□□□□□□□□■
■■■■■■■■■■■■■
>>682 >>700 稜の長さを { A, A, (S/2A - A)/2 } とおく。
(S/2A - A)/2 が自然数となるAを n個以上とれるように Sを決める。
稜 … 多面体の辺
{(x,y,z)|x+y+z=n、x,y,z は非負整数、n は1以上の整数}
を満たす格子点の集合をAとする。
Aから異なる三点を選んだとき、それが正三角形を成している確率を n で表せ。
答えは、プログラムを組めば予想可能なものになるので、答えのみの解答は認めないものとする。
Oを中心とする半径1の円周上に、n個の点P[1],P[2],...,P[n]を、以下の2条件をともに満たすように配置する。なお各点はこの順に反時計回りに配置されるものとする。
(ア)各線分P[i]P[i+1]の長さは全て等しい。すなわちP[0]P[1]=P[1]P[2]=...=P[n-1]P[n]である。
(イ)0°<∠P[1]OP[n]≦180°
n以下の各自然数iに対し、△OP[i-1]P[i]の重心をG[i-1]とおく。
このとき、以下の(A)が成り立つように辺P[0]P[1]の長さを定めることができるか。
(A)相異なる整数jとkをうまく選べば、2点P[j]とP[k]を通る直線で、その上にG[0],G[1],...,G[n-1]の少なくとも1つが乗るようにできる。
すいません先程の問題文がおかしかったので訂正します。
Oを中心とする半径1の円周上に、n個の点P[1],P[2],...,P[n]を、以下の2条件をともに満たすように配置する。なお各点はこの順に反時計回りに配置されるものとする。
(ア)各線分P[i]P[i+1]の長さは全て等しい。すなわちP[1]P[2]=P[2]P[3]=...=P[n-1]P[n]である。
(イ)0°<∠P[1]OP[n]≦180°
n-1以下の各自然数iに対し、△OP[i]P[i+1]の重心をG[i]とおく。
このとき、以下の(A)が成り立つように辺P[1]P[2]の長さを定めることができるか。
(A)相異なる整数jとkをうまく選んで2点P[j]とP[k]を通る直線を引けば、その上にG[1],G[2],...,G[n-1]の少なくとも1つが乗る。
>>705 求める確率をp[n]とすると
p[n]=2/(n^2+3n-2)
になると予想した
A[n]={(x,y,z)|x+y+z=n, x,y,zは非負整数}
できる正三角形の個数をT[n]とすると、
最初の方は
T[1]=1, T[2]=5, T[3]=15, T[4]=35, T[5]=70
となった
A[n]と△型・▽型の正三角形の個数は規則的に数えられるけど
傾いてる正三角形が一般の場合にうまくいかないorz
>>708
辺長L(≧2)の△型には、傾いた正三角形(L-1)個が内接する。(▽も含む)
>>705
A[1] = 3,
A[n] = A[n-1] + (n+1),
より
A[n] = (n+2)(n+1)/2, … 三角数
A[n]個の点から3点を選ぶ方法は
C[A[n], 3] = A[n] (A[n]-1) (A[n]-2)/6
= {(n+2)(n+1)/2} {(n+3)n/2} {(nn+3n-2)/2},
辺長nの大きい△型の中に
辺長Lの△型が C[n+2-L, 2] 個ある。
傾いている正三角形も含めれば、そのL倍になる。
T[n] = Σ(L=1, n) C[n+2-L, 2]・L
= C[n+3, 4]
= (n+3)(n+2)(n+1)n/24
= A[n](A[n]-1)/6,
よって
T[n]/C[A[n], 3] = 1/(A[n]-2) = 2/(nn+3n-2), ご名答
>> 辺長L(≧2)の△型には、傾いた正三角形(L-1)個が内接する。(▽も含む)
ここがポイントですね。傾かないものも含めると、
「サイズLの正置な正三角形には、調度L個の正三角形が属す」
と言えます。全ての正三角形は、いずれかの正置な正三角形に属すため、
あとは、正置な正三角形がいくつあるかを調べ、足し合わせるだけです。
>>709,710
なるほど、そうやって考えるんですね
C[n+2-L, 2]の部分ですが、これは
辺長Lの正置な正三角形のいちばん上の辺長1の正三角形に注目して
Σ[k=1,n-(L-1)]k
と数えたものでしょうか?
サイズ n の正置な正三角形は 1 (=C[2,2])
サイズ n-1 の正置な正三角形は 3 (=1+2=C[3,2])
サイズ n-2 の正置な正三角形は 6 (=1+2+3=C[4,2])
サイズ n-3 の正置な正三角形は 10 (=1+2+3+4=C[5,2])
...
サイズ 1 の正置な正三角形は 1+2+3+...+n=C[n+1,2]
です。では、サイズ L では? というと、 C[n+2-L,2] という事です。
注目するサイズの正置正三角形のトップの頂点の、可動範囲を数え上げるという考えでもokですね。
>>682 用意していた答え
3辺の長さを (a,b,c) = (1, 2^r-1, 2^{2n-r}-1)、r=1,2,…n とおくと、
表面積 S = 2(ab+bc+ca) = 2(2^{2n}-1).
■■■■■■■■■■■■■
□□□□□□□□□□□□■
■■■■■■■■■■■□■
■□□□□□□□□□■□■
■□■■■■■■■□■□■
■□■□□□□□■□■□■
■□■□■■■□■□■□■
■□■□■□□□■□■□■
■□■□■■■■■□■□■
■□■□□□□□□□■□■
■□■■■■■■■■■□■
■□□□□□□□□□□□■
■■■■■■■■■■■■■
>>580
山札からダイヤが12枚出たところまですべて1/4で
13枚目のみゼロにすることも可能
■箱の中のカードがダイヤである確率は
基本形の式
q=1-{{165n-3n^2+351}/(208n-7n^2+468)}に
係数αをnの各項に掛ける
q=1-{{165nα-3αn^2+351}/(208nα-7αn^2+468)}
351と468にはそれぞれβ=479001600を掛ける
∵q=1-{{165nα-3αn^2+351β}/(208nα-7αn^2+468β)}
α=(n^2-13n)^6+182(n^2-13n)^5+13468(n^2-13n)^4
+516360(n^2-13n)^3+10752768(n^2-13n)^2+114341760(n^2-13n)
+479001600
これで出来上がり どうして確率や場合の数の問題しか出てこないのかね。
そんなに面白いかい?
AとBが引き分けのないゲームを次々と行い、一回のゲームで勝つ確率はそれぞれa, bである。つまりa+b=1である。
Aが先にn勝に到達する確率を求めよ。
>>718 これ求まるん?
1/2の時でもバナッハのマッチ箱で超難題なのに。
1/2じゃなくて求まるん?
先にn勝というのは、2n-1回やってn勝以上することと同じ
Σ[k=n~2n-1] a^k・b^(2n-1-k)・C(k,2n-1)
何も難問じゃない
将棋の番勝負の勝率レーティングから推計したことあるやつなら簡単にわかるはず
あ、失礼。単にAが勝つ確率か。回数の期待値と勝手に思った。勝つ確率だけなら出るかな?
>>721,724
p(n)=Σ[k=n,2n-1]a^k・b^(2n-1-k)・C(k,2n-1)
とおくと、n≧2のとき二項定理より
(a+b)^(2n-1)=2(p(n)-a^n・b^(n-1))+a^n・b^(n-1)
よって
p(n)=(1+a^n・b^(n-1))/2
>>726 二項係数抜けてるしそもそも3行目ダメですね
撤回します
とりあえず10項ほど計算させてみたけど
makelist(factor(expand(sum(binomial(2*n-1,k)*a^k*(1-a)^(2*n-1-k),k,n,2*n-1))),n,1,10);
[
a,
-a^2*(2*a-3),
a^3*(6*a^2-15*a+10),
-a^4*(20*a^3-70*a^2+84*a-35),
a^5*(70*a^4-315*a^3+540*a^2-420*a+126),
-a^6*(252*a^5-1386*a^4+3080*a^3-3465*a^2+1980*a-462),
a^7*(924*a^6-6006*a^5+16380*a^4-24024*a^3+20020*a^2-9009*a+1716),
-a^8*(3432*a^7-25740*a^6+83160*a^5-150150*a^4+163800*a^3-108108*a^2+40040*a-6435),
a^9*(12870*a^8-109395*a^7+408408*a^6-875160*a^5+1178100*a^4-1021020*a^3+556920*a^2-175032*a+24310),
-a^10*(48620*a^9-461890*a^8+1956240*a^7-4849845*a^6+7759752*a^5-8314020*a^4+5969040*a^3-2771340*a^2+755820*a-92378)
]
なんにも思いつかんorz。
あかん、いろいろ調べたけどどうしようもなさそう。
>>721で正解なんかな?
pを有理数とする。3辺の長さがp,p,1の二等辺三角形をT(p)と書く。
ある自然数kが存在して、k個のT(p)のみに分割できる多角形全体からなる集合をS(k)とする。
k=1,2,3,...に対し、以下の条件を満たすS(k)の要素の多角形の形状をすべて決定せよ。
条件『多角形の任意の2頂点間の距離は有理数である。』
>>718 Aが先にn勝する確率をPnとすると、
P1=a
P2=a^2+2a^2・b
P3=a^3+3a^3・b+6a^3・b^2
P4=a^4+4a^4・b+(5C2)a^4b^2+(6C3)a^4・b^3
=a^4+4a^4・b+10a^4b^2+20a^4・b^3
P5=a^5+5a^5・b+(6C2)a^5・b^2+(6C3)a^5・b^3+(6C4)a^5・b^4
=a^5+5a^5・b+15a^5・b^2+20a^5・b^3+15a^5・b^4
P6=a^6+6a^6・b+(7C2)a^6・b^2+(7C3)a^6・b^3+(7C4)a^6・b^4+(7C5)a^6・b^5
=a^6+6a^6・b+21a^6・b^2+35a^6・b^3+35a^6・b^4+21a^6・b^5
P7=……
前
>>624フィボナッチだな。一般項出るぞ。
■□■■■□■■■□■■■□■■■
■□■□■□■□■□■□■□■□■
■■■□■■■□■■■□■■■□■
P1=a
P2/a^2=1+2b
P3/a^3=1+3b+6b^2
P4/a^4=1+4b+(5・4/2・1)b^2+(6・5・4/3・2・1)b^3
P5/a^5=1+5b+(6・5/2・1)b^2+(6・5・4/3・2・1)b^3+(6・5/2・1)b^4
P6/a^6=1+6b+21b^2+35b^3+35b^4+21b^5
P7/a^7=1+7b+28b^2+56b^3+70b^4+56b^5+28b^6
P8/a^8=1+8b+36b^2+84b^3+126b^4+126b^5+84b^6+36b^7
P9/a^9=1+9b+45b^2+120b^3+210b^4+252b^5+210b^6+120b^7+45b^8
P10/a^10=1+10b+55b^2+165b^3+330b^4+462b^5+462b^6+330b^7+165b^8+55b^9
前
>>731漸化式ができそう。
nが奇数のとき、
Pn/a^n=
nが偶数のとき、
Pn/a^n=
>>721
p(n) = Σ[k=n, 2n-1] a^k b^(2n-1-k) C(2n-1, k), (b=1-a)
p(n+1) = p(n) + C[2n-1, n] (a-b)(ab)^n, (b=1-a) ∂p(n)/∂a = (n/2) C(2n, n) {a(1-a)}^(n-1),
p(n) = (n/2) C(2n, n) Σ[k=0, n-1] (-1)^k C(n-1, k)/(n+k) a^(n+k)
= (n/2) C(2n, n) a^n Σ[k=0, n-1] C(n-1, k)/(n+k) (-a)^k,
前
>>733訂正。
P10/a^10=1+10b+(11C2)b^2+(12C3)b^3+(13C4)b^4+(14C5)b^5+(15C6)b^6+(16C7)b^7+(17C8)b^8+(18C9)b^9
=1+10b+55b^2+220b^3+715b^4+2002b^5+5005b^6+11440b^7+24310b^8+48620b^9
P9/a^9=1+9b+(10C2)b^2+(11C3)b^3+(12C4)b^4+(13C5)b^5+(14C6)b^6+(15C7)b^7+(16C8)b^8
=1+9b+45b^2+165b^3+495b^4+1287b^5+(14C6)b^6+(15C7)b^7+(16C8)b^8
P8/a^8=1+8b+36b^2+120b^3+(11C4)b^4+(12C5)b^5+(13C6)b^6+(14C7)b^7
P7/a^7=1+7b+(8C2)b^2+(9C3)b^3+(10C4)b^4+(11C5)b^5+(12C6)b^6
=1+7b+28b^2+84b^3+(10C4)b^4+(11C5)b^5+(12C6)b^6
P6/a^6=1+6b+(7C2)b^2+(8C3)b^3+(9C4)b^4+(10C5)b^5
P5/a^5=1+5b+(6C2)b^2+(7C3)b^3+(8C4)b^4
=1+5b+15b^2+35b^3+56b^4
>>718 Rを使うと 負の二項分布を使ってpnbinom(n-1,n,a)で数値計算はできる。
>>718 前
>>736一般項が出た。
Pn=a^n/(n-1)!Σ[k=1~n-2]{(n+k)!b^(k+1)}/(k+1)!
>>735 おお、すごい。
流石にこれ以上は無理?
>>735 makelist((expand(sum(binomial(2*n-1,k)*a^k*(1-a)^(2*n-1-k),k,n,2*n-1))),n,0,10);
makelist((expand(n/2*a^n*binomial(2*n,n)*sum(binomial(n-1,k)/(n+k)*(-a)^(k),k,0,n-1))),n,0,10);
(%o1) [0,a,3*a^2-2*a^3,6*a^5-15*a^4+10*a^3,-20*a^7+70*a^6-84*a^5+35*a^4,70*a^9-315*a^8+540*a^7-420*a^6+126*a^5,-252*a^11+1386*a^10-3080
*a^9+3465*a^8-1980*a^7+462*a^6,924*a^13-6006*a^12+16380*a^11-24024*a^10+20020*a^9-9009*a^8+1716*a^7,-3432*a^15+25740*a^14-83160*a^13+
150150*a^12-163800*a^11+108108*a^10-40040*a^9+6435*a^8,12870*a^17-109395*a^16+408408*a^15-875160*a^14+1178100*a^13-1021020*a^12+556920*
a^11-175032*a^10+24310*a^9,-48620*a^19+461890*a^18-1956240*a^17+4849845*a^16-7759752*a^15+8314020*a^14-5969040*a^13+2771340*a^12-
755820*a^11+92378*a^10]
(%o2) [0,a,3*a^2-2*a^3,6*a^5-15*a^4+10*a^3,-20*a^7+70*a^6-84*a^5+35*a^4,70*a^9-315*a^8+540*a^7-420*a^6+126*a^5,-252*a^11+1386*a^10-3080
*a^9+3465*a^8-1980*a^7+462*a^6,924*a^13-6006*a^12+16380*a^11-24024*a^10+20020*a^9-9009*a^8+1716*a^7,-3432*a^15+25740*a^14-83160*a^13+
150150*a^12-163800*a^11+108108*a^10-40040*a^9+6435*a^8,12870*a^17-109395*a^16+408408*a^15-875160*a^14+1178100*a^13-1021020*a^12+556920*
a^11-175032*a^10+24310*a^9,-48620*a^19+461890*a^18-1956240*a^17+4849845*a^16-7759752*a^15+8314020*a^14-5969040*a^13+2771340*a^12-
755820*a^11+92378*a^10]
素晴らしい。
n=0,αn/βn,α={2^n+2^(n-1)},β={2^(n+2)+2^(n-1)}
分母と分子の両方にゼロ掛けているのに
なんで1/3が出力されるねん?(´・ω・`)
(1)実級数Σ_{n=1}^∞ a_nが絶対収束するならば
Σ_{n=1}^∞ (a_n)^2は収束するか?
(2)実級数Σ_{n=1}^∞ a_nが条件収束するならば
Σ_{n=1}^∞ (a_n)^2は収束するか?
(1) a_n > 1 である n は有限個なのでそれらを除いて (a_n)^2 ≦ a_n。よって収束する。
(2) しない。反例:a_n = (-1)^n/√n。
間違ってるものを採点して生徒が伸びた方がいたと思う。
高速通信添削で赤入れるみたいにしちゃうといい。女子美味しいな。
前
>>738 Pn(n-1)!/a^n=(n+1)n(1-a)^2/2・1+(n+2)(n+1)n(1-a)^3/3・2・1+……+(2n-2)(2n-3)……n(1-a)^(n-1)/(n-1)!
Pn={a^n/(n-1)!}{(n+1)n(1-a)^2/2・1+(n+2)(n+1)n(1-a)^3/3・2・1+……+(2n-2)(2n-3)……n(1-a)^(n-1)/(n-1)!}
通分するのかな。
>>743 (2)
S = Σ_{n=1}^{∞} a_n = Σ_{n=1}^{∞} (-1)^n /√n が収束すること。
S = -1 + 1/√2 - Σ_{m=2}^{∞} ( 1/√(2m-1) - 1/√(2m) )
> -1 + 1/√2 - (1/2)Σ_{m=2}^{∞} ( 1/√(2m -3/2) - 1/√(2m +1/2) ) … (*)
= -1 + 1/√2 - 1/√10
= -0.60912098483…
S = -1 + Σ_{m=1}^{∞} ( 1/√(2m) - 1/√(2m+1) )
< -1 + (1/2)Σ_{m=1}^{∞} ( 1/√(2m -1/2) - 1/√(2m +3/2) ) … (*)
= -1 + 1/√2 - 1/√3 + 1/√14
= -0.60298224609…
S = -0.60489864342163… >>748 (補足)
f(n) = 1/√n の平均変化率 {1/√(n-h) - 1/√(n+h)}/(2h) が h>0 と共に増加すること。
{f(n-h) - f(n+h)}/2h = {1/√(n-h) - 1/√(n+h)}/(2h)
= {√(n+h) - √(n-h)}/{2h √(nn-hh)}
= 1 / {√(nn-hh)・(√(n-h) + √(n+h)}
= 1 / {√(nn-hh)・√[2n+2√(nn-hh)]},
あるいは平均値の定理により
f(n-L-h) - f(n+k+h) - {f(n-h) - f(n+h)} - {f(n-L+k-h) - f(n-L+k+h)} + {f(n+k-L) - f(n-L+h)}
= {f(n-L-h) -f(n-h) -f(n-L+k-h) +f(n+k-h)} - {f(n-L+h) -f(n+h) -f(n-L+k+h) +f(n+k+h)}
= -2h {f '(a-L) - f '(a) - f '(a-L+k) + f'(a+k)} (n-h<a<n+h)
= -2h {f '(a-L) - f '(a)} -2h {f '(a-L+k) - f '(a+k)}
= 2hk {f "(b-L) - f "(b)} (a<b<a+k)
= -2hkL f '''(c) (b-L<c<b)
> 0 [0,π]上の連続関数fに対して、
lim(n→∞)∫_0^π f(x)cos(nx) dx=0
となることを証明せよ
>>751 (p,q) := 2/π∫ pq dx とする。
これは双線形であり、{cos nx} は (cos lx, cos mx) = δ(l,m) となる。
Nを自然数とし
a[n] = (cos nx, f)、g = Σ[m:1~N] a[m] cos mx、h = f-g とおく。
n: 1~N に対し
(h, cos nx) = (f-g, cos nx) = (f, cos nx) - (Σ[m:1~N] a[m] cos mx, cos nx) = a[n] - a[n] = 0
であるから (h,g) = 0 である。
よって
(f, f) = (g+h, g+h) = (g, g) + 2(g, h) + (h, h) = (g, g) + (h, h) ≧ (g, g) = (Σ[l:1~N] a[l] cos lx, Σ[m:1~N] a[m] cos mx) = Σ[m:1~N] a[m]^2
である。
これが任意のNで成立するから
Σ[m:1~∞] a[m]^2
は収束するので lim(n→∞)a[n]=0 である。
>>751 正解!
ベッセルの不等式証明してくれた感じかな
【世界教師マⅰトレーヤ】 トランプは現在、ツイートを囮にして、史上最悪の法案にサインする気でいる
http://2chb.net/r/liveplus/1538533045/l50 山本太郎もブチ切れる、労働者へのゲスい裏切り!
>>734
p(n+1) - p(n) = (2a-1) C[2n-1, n] (a(1-a))^n, (n≧1)
の両辺に t^n を掛けて和をとると
G(t)/t - p(1) - G(t) = (2a-1)Σ[n=1,∞] C[2n-1, n] (a(1-a)t)^n
= (1/2)(2a-1) {1/√(1-4a(1-a)t) -1}, … (*)
(2(1-t)/t) G(t) = 1 + (2a-1)/√(1-4a(1-a)t),
G(t) = Σ[n=1,∞] p(n) t^n = (t/2(1-t)) {1 + (2a-1)/√(1-4a(1-a)t)},
*) 一般化された二項定理
1/√(1-4x) = 1 + 2Σ[n=1,∞] C[2n-1, n] x^n, >>718 の答えは今出てる答えで正解でいいのかな?
流石にもうこれ以上はどうしょうもない気がする。
>>755 >>718の答え、
>>747でいいの?
確率をnとaで表せってことだよね?
……があるままでいいってこと?
通分して分子が簡単になったりして。
前
>>747 前
>>757 通分すると、
Pn={a^n/(n-1)!(n-1)!}[(n+1)!{(n-1)(n-2)……3}(1-a)^2+(n+2)!{(n-1)(n-2)……4)}(1-a)^3+……+(2n-2)!(1-a)^(n-1)]
簡単にならないなら……を許可するしかないか。それかΣとkを使うか。
>>756 Catalan(n) = C[2n, n] - C[2n, n-1] = {1/(n+1)} C[2n, n]
Σ[n=0,∞] Catalan(n) t^n = {1 - √(1-4t)}/(2t),
このスレで見つけた問題。
[0,n]×[0,n]の格子点の隣接する格子点をむすんで得られるグラフを考える。(図1参照)
このグラフの左下と右上を結ぶグラフ上の経路で長さ2nのもののうちy≦xの部分にある横線をちょうどk回通るものの個数を求めよ。
>>432より
>―図1―(n=6の場合)
>┌─┬─┬─┬─┬─┬─┐
>│ │ │ │ │ │ │
>├─┼─┼─┼─┼─┼=┤
>│ │ │ │ │ │ │
>├─┼─┼─┼─┼=┼=┤
>│ │ │ │ │ │ │
>├─┼─┼─┼=┼=┼=┤
>│ │ │ │ │ │ │
>├─┼─┼=┼=┼=┼=┤
>│ │ │ │ │ │ │
>├─┼=┼=┼=┼=┼=┤
>│ │ │ │ │ │ │
>└=┴=┴=┴=┴=┴=┘
■■■■■■■■■■■■■
□□□□□□□□□□□□■
■■■■■■■■■■■□■
■□□□□□□□□□■□■
■□■■■■■■■□■□■
■□■□□□□□■□■□■
■□■□■■■□■□■□■
■□■□■□□□■□■□■
■□■□■■■■■□■□■
■□■□□□□□□□■□■
■□■■■■■■■■■□■
■□□□□□□□□□□□■
■■■■■■■■■■■■■
不思議な現象に遭遇したけど、よくわからないのでみんなの知恵を借りたい。
a1,a2,…を不定元とし、σをその添字を1だけ大きくする作用素とする。
次で有理式の列{F[n]; n=0,1,2,…}を定める:
F[0] = 1, F[n] = (F[n-1] + σF[n-1])/(a1+a2+…+an) (n≧1)。
F[1] = (1 + 1)/(a1) = 2/a1,
F[2] = (2/a1 + 2/a2)/(a1+a2) = 2/a1a2,
F[3] = (2/a1a2 + 2/a2a3)/(a1+a2+a3) = 2(a1+a3)/a1a2a3(a1+a2+a3),
F[4] = (2(a1+a3)/a1a2a3(a1+a2+a3) + 2(a2+a4)/a2a3a4(a2+a3+a4))/(a1+a2+a3+a4)
= 2(a1a2+a2a3+a3a4)/a1a2a3a4(a1+a2+a3)(a2+a3+a4)
のようになるが、既約分数表示での分母を見ると偶数項の因数は約分で消え、奇数項の因数しか現れていない。
PCで調べるとF[8]まではそうなっている。
なので「F[n]を既約分数で表したとき分母には奇数項の因数しか現れない」と予想するが、
これは正しいだろうか?
また関連しそうなことがあったら教えてください。
1/a(a+b)(a+b+c)…(a+b+c+…+z) を [a,b,c,…,z] と書くことにする。
[] = 1,[a] = 1/a, [a,b] = 1/a(a+b) など。
次を示せ。
(1) [a][b] = [a,b] + [b,a]
(2) [a,b][x] = [a,b,x] + [a,x,b] + [x,a,b]
(3) [a,b][x,y] = [a,b,x,y] + [a,x,b,y] + [a,x,y,b] + [x,a,b,y] + [x,a,y,b] + [x,y,a,b]
(4) [a][b][c] = [a,b,c] + [a,c,b] + [b,a,c] + [b,c,a] + [c,a,b] + [c,b,a]
また、一般にどのようなことがいえるだろうか?
(
>>763 を考えた背景にあるもの)
E, A, B を同じ型の正方行列とし、Eを単位行列とする。
E-ABが逆行列Cをもつとき、E-BAが正則であることを示し、その逆行列をE, A, B, Cを用いて表せ。
>>765 C = (E-AB)^-1 = E + AB + (AB)^2 + … とおもえば
(E-BA)^-1 = E + BA + (BA)^2 + … = E + BA + B(AB)A + B (AB)^2 C + … = E + BCA と予想できて、
あとは計算で (E-BA)(E+BCA) = (E+BCA)(E-BA) = E。
A,Bがn次行列のとき、ABとBAの固有値は等しいことを示せ。
係数環がZで証明できれば十分。
よってさらにCで証明できれば十分。
Aが正則のときABA^(-1)とBの固有多項式が等しく故成立。
一般の場合は等式 ch AB = ch BA がザリスキ開集合 det A≠0 で成立する故一般に成立。
■ニャンティホール問題
□□□ ∧,,∧ ∧,,∧
□□□ (,,・∀・) ミ,,・∀・ミ
□□□~(_u,uノ @ミ_u,,uミ
>>763 それ無理じゃね?
全変数に1をいれるとF[n] = 2^n/n!なので十分大きいnでv_2(F[n]) < 0。
一方でa1 = 1、残りに2をいれると全てのnでF[n]は2進整数。
よって分母に必ず項の数が偶数の因子が出てくると思う。
>>770 > 全変数に1をいれるとF[n] = 2^n/n!なので十分大きいnでv_2(F[n]) < 0。
v_2は2進付値だよね。だったら、
v_2(n!) = Σ[k=1,∞] floor(n/2^k) ≦ Σ[k=1,∞] n/2^k ≦ n だから
v_2(F[n]) ≧ 0 だよ。
p1, p2, Pは素数かつ、
p1 ≧ 3, p2 ≧ 3, P ≧ 7で、
p1 + p2 = ( P + 1 )
が成り立つときの
p1, p2, P がみたす性質って何かありますか?
>>767 Aが正則でないとき…
Eをn次の単位行列、yは実数とする。
|A+yE| はyのn次式だから、|A+yE| = 0 を満たすyの個数は高々n個である。
|A+yE|≠0 となるyに対しては
|xE - (A+yE)B| = |xE - B(A+yE)|,
が成り立つ。|A+yE| = 0 の解をうまく避けながら y→0 とすれば、
|xE-AB| = lim_{y→0} |xE - (A+yE)B| = lim_{y→0} |xE - B(A+yE)| = |xE-BA|,
∴ |xE-AB| = |xE-BA|.
A,B∈M_n(C)に対して ABとBAの固有多項式が同じになることを証明せよ。
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1239473677 任意のn次正方行列A,Bについて ABとBAの固有多項式が同じになることの証明
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11107489021 nを自然数として、a_1=3,a_n=n(a_(n-1)-1)+2 (n≧2)でa_nを定める。
ここK村の人口はa_n人で、増えることも減ることもない。
さて、K村から任意の2人を選んだ時、その2人はある「関係」を持っているとする。そして、その「関係」はn種類にわたって存在する。
この時、どの2人を選んでも同じ「関係」で結ばれているような3人組が必ず存在することを示せ。
オリジナルです
考え方自体は既出だと思う
a[1]=3人だと1種類
a[2]=6人だと2種類
a[3]=17人だと3種類
・・・
>>778が
>>781の意味ならそのままwikiに書いてある漸化式で解けちゃうね。R(…)の中の2は自動的に落ちてしまう
清書
Claim 1)
R(k1,…,kn)≦R(k1-1,k2,…,kn) + R(k1,k2-1,…,kn) + … + R(k1-1,k2,…,kn-1) - n + 2
(∵) R(k1-1,k2,…,kn) + R(k1,k2-1,…,kn) + … + R(k1-1,k2,…,kn-1) - n + 2個の点からなる完全グラフから1点v を選び、そこから残りの点への辺を1~nに彩色する。
このとき、色1に塗られている辺の個数がR(k1-1,k2,…,kn)以上かまたは…色nに塗られている辺の個数がR(k1-1,k2,…,kn-1)以上である。
最初の場合(残りの場合も同じように議論できる)、色1に塗られている辺の向かう先の点の個数がR (k -1, k2,…,kn)以上だから、それらの点からk1 -1個の点の、色1のみからなる完全グラフか、ki個の点の色iのみからなる完全グラフがある。
前者の場合、v とあわせればk1 個の点の色1のみからなる完全グラフが得られる。
Claim2)
R(k1,…,kn,2) = R(k1,…,kn)
(∵) R(k1,…,kn)個以上の頂点からなる完全グラフをn+1色に塗り分ける時、色n+1が使われていればその辺のみからなるグラフが2点完全グラフである。
n+1がつかわれていなければR(k1,…,kn)の定義からいずれかの色 i のみで塗られた完全 ki グラフを含む。
以上により R(3,3,…,3) ≦ a_n。
わかスレの問題改題。
数列 (c[n], d[n]) を
c[n] = (2n-1)c[n-1] + c[n-2]、c[1] = 0、c[2] = 1、
d[n] = (2n-1)d[n-1] + d[n-2]、d[1] = 1、d[2] = 0
で定める時 lim[n→∞] c[n]/(2n-1)!!、lim[n→∞] d[n]/(2n-1)!! を求めよ。
>>788 c[n]の方は組合せ的意味(
http://2chb.net/r/math/1534342085/494,510,623)を考えれば、
c[n] = Σ[r=0,n] (-1)^r binomial(2n-r,r) (2n-2r)! / (n-r)!2^(n-r) が分かって、
α(n,r) := n!(2n-r)!2^r/(2n)!(n-r)! が
0 < α(n,r+1) < α(n,r), α(n,r)→1 (n→∞) となるのを使えば
lim[n→∞] c[n]/(2n-1)!! = lim[n→∞] Σ[r=0,n] ((-1)^r/r!)α(n,r) = e^(-1)。
>>289 おお、なるほど。
素晴らしい。
それなら前スレででてきたベッセル関数もへったくれもなしに証明できますね。
今の所用意している解答はベッセル関数もへったくれもある解答です。
d[n]の方もそんな感じでできるかもしれないですね。
ジョーカーを除いたトランプ52枚を外からは中が
確認できない52個の箱の中に表を見ないで一枚ずつ入れた
そして、52個の箱の中から適当に三つの箱を選んで三枚の
カードを取り出すと三枚ともダイヤであった
このあと残りの49個の箱の中からどの箱を選んでも
箱の中のダイヤの確率は10/49である
a,b (1≦a≦b) を整数とする。
b階建てビルのエレベーターは1階からb階までを移動している。
a階でエレベータを待つとき、上からやってくる確率を求めよ。
縦3マス、横4マスの12マスのうちランダムに選ばれた2マスにそれぞれ宝が眠っている。
AEIBFJ…の順で縦に宝を探していく方法をとるP君と、ABCDEFGH…の順で横に宝を探していく方法をとるQ君が、同時に地点Aから探索を開始した。
どっちの方が有利?
ABCD
EFGH
I JK L
>>795 移動時間とかなんにも条件ないならイーブン。
>>795
以外に自明じゃないけど結局イーブン
P : AEIBFJCGKDHL
Q : ABCDEFGHIKKL
部屋 : ABCDEFGHIKKL
先に入る:△QQQPPQQPPP△ ABCDEFGHIJKLとBCDEFGHIJKLAの争いがえぐい
ETFJKをP部屋と呼ぶ。Pはこの部屋にQより先にこの順に入室する。
BCDGHをQ部屋とよぶ。Qはこの部屋にPより先にこの順に入室する。
Aに宝があれば同着でイーブン。
Aに宝がなくLに宝があれば残りがP部屋か、Q部屋かによるのでイーブン。
2つともP部屋ならP勝ち、2つともQ部屋ならQ勝ちでその確率はイーブン。
のこり25通りは
EIFJK
B△
C △
D △
G △
H △
と5×5マスからひとつ選ぶ場合だけど△の組み合わせなら同着、
上半分ならQ勝ち、下半分ならP勝ちでイーブン。
以外に思ったより自明じゃないなぁ。
>>795 追記。問題文にあるように、ABCDEFGH…とAEIBFJ…という探索方法をとっています。P君はQ君が先にBを調べていても4ターン目にちゃんと調べることになってますよ。
要するに、相手が調べ終わった部屋も重複して調べる場合が出てきます。
>>797 いや完全に自明だろw
全ての箱等価なんだから
くじ引きと同じだぞ
>>801 全く自明じゃないよ、1マスにしか宝がないなら自明だが2マスあれば自明じゃない。
結論はネタバレになるから言わないけど案外面白い結果になる。
>>802 壮絶なバカだなあ
マスを箱と考える。
箱のセットをコピーして、A~Lのセットを2つ用意する
アタリとなっているの箱の文字はどちらも同じ。
P : AEIBFJCGKDHL
Q : ABCDEFGHIJKL
PQはどの順番でハコを開けていくか?が同じだけ。
ハコの中身がランダムで未知なのに開ける順番で差がつきうるとかお笑いだなw
盛大に誤字ったw
どの順番でハコを開けていくか?が違うだけ が正しい
>>803 >箱のセットをコピーして、A~Lのセットを2つ用意する
それ違う問題だろ。
本問の場合片方が先に見つけたお宝は他方の手には入らない
それを踏まえた上で
P:ABCDEFGHIJKL
Q:BCDEFGHIJKLA
これでもイーブンだと思う?
>>804 あーごめん、完全に自分のミスです
先に宝を見つけた方が勝ちです。
いずれか1人が(あるいは同時に2人が)宝を見つけた時点でゲームは終了です。すいません。
>>806 100%イーブンだろwwww
頭悪いんだなw
お前の言ってるのは
「クジ引きで後に引くのは不利、先に当たりひかれちゃうかもしれないから!」
これと完全に同レベルな
>>806 マジで分からないのか?
お前の言ってるのは
「どれが当たりか全く分からない12個の箱を、開ける順番を変えるだけで
当たり引くまでの回数の期待値を変えられる」
ってことだぞ?
本気で言ってんならヤバいよw
>>808 P:ABCDEFGHIJKL
Q:BCDEFGHIJKLA
この順に部屋を調べるとして、1個だけのお宝が
A~Lにある10の場合それぞれについて
P、Q のどちらが勝つかわかる?
Aにある場合→Pが先に調べるからの勝ち
Bにある場合→同様にPの勝ち
...
のように
>>810 >Aにある場合→Pが先に調べるからPの勝ち
>Bにある場合→Qが先に調べるからQの勝ち
の間違いだった
>>809 2マスに宝がそれぞれ置いてあるんですよ??もちろん1マスにしかないならイーブンですが、2マスに宝がある場合、この2つの宝は互いに独立して配置されるわけではないんですよ。
要するに、宝が1マスに重複して置かれることがないから「宝Aがあるマスに配置された瞬間、宝Bはそのマス以外に配置されることになる」わけで、その期待値で考える理屈は通用しませんよね。
>>809 1つの当たりが10個の箱に入っているとして、
P:ABCDEFGHIJKL
Q:BCDEFGHIJKLA
このように片方が開ける順よりも1つ先の箱を開けることによって、
Qが当たりを引くまでの手数は
1/10の確率でPより9増える (当たりがAの場合)
9/10の確率でQより1減る
双方の当たりを引くまでの手数の期待値は変わらないが、
他方より1でも少なければ勝ちなのでQが勝つ確率は9/10となる
>>813 >9/10の確率でQより1減る
Pより1減る、の間違いだな
なんかグダグダ
宝が一つの場合でも
>>810>>811みたいなのを考えると単純な期待値の問題にはならないんじゃ?
>>815 その場合は「相手が調べ終わっている箱を確かめる」回数が多い方が負けるでしょうね、、
あれ?
>>799で終わったと思ってるんだけど?
間違ってる?
コレ、直感的には自明にイーブンに見えるけど、ちゃんと考えると少なくとも自明じゃないのが面白い。
けど結局イーブンだからなぁ。
縦横でも
P:AEIJFBCGKLHD
Q:ABCDHGFEIJKL
とかにしてイーブンじゃない設定の方が良かったかも。
いや、嘘書いた。
>>799の残り25通りイーブンじゃないやん。
BEが宝箱ならQ部屋のBにQが入室すらのが2ターン目、EにPが入室するのが6ターン目だからQの勝ち。
同様にして勝敗を埋めて行くと
EIFJK
B QQQQQ
C QQQQQ
D QQQQQ
G PPQQQ
H PPPPQ
となってQの勝ちですね。
直感に反してて面白い。
いや、合ってる。
やっぱり頭の中だけで考えるとダメだ。
ALは無視して残り10部屋で45通り。
P部屋五部屋のみから選ぶのが10通り。
Q部屋五部屋のみから選ぶのが10通り。
残りは25通り、Q勝ちの方が多い。
なるほどねえ
確かにQの方が微妙に先に見つける場合が多いな
Pが先に見つけるのは以下の26通り
CE,DE,DI,EF,EG,EH,EI,EJ,EK,EL,FG,FH,FI,FJ,FK,FL,GI,GJ,HI,HJ,IJ,IK,IL,JK,JL,KL
Qが先に見つけるのは以下の27通り
BC,BD,BF,BG,BH,BI,BJ,BK,BL,CD,CF,CG,CH,CJ,CK,CL,DF,DG,DH,DJ,DK,DL,GH,GK,GL,HK,HL
同時に見つけるのは以下の13通り
AB,AC,AD,AE,AF,AG,AH,AI,AJ,AK,AL,BE,CI
何を数え上げているのさっぱりわからんが、12C2=121なので121通りないとおかしい。
イーブンだぞ。
>>788,789,791
e[n] = Σ[r=0,n] binomial(2n-r,r) (2n-2r)! / (n-r)!2^(n-r) と置くと、c[n], d[n]と同じ漸化式
e[n] = (2n-1)e[n-1] + e[n-2] が成り立ち、e[1]=2, e[2]=7 であるから d[n] = (e[n]-7c[n])/2。
>>789 と同様にして lim[n→∞] e[n]/(2n-1)!! = lim[n→∞] Σ[r=0,n] (1/r!)α(n,r) = e であるから
lim[n→∞] d[n]/(2n-1)!! = (e-7e^(-1))/2。
c[n]などはいろいろな表し方がある:
c[n] = Σ[r=0,n] (-1)^(n-r) binomial(n+r,2r) (2r)! / r!2^r
= Σ[r=0,n] (-1)^(n-r) binomial(n+r,2r) (2r-1)!! (ただし (-1)!!=1 とする。)
0以下に延長すると:
e[-5]=266, e[-4]=37, e[-3]= 7, e[-2]=2, e[-1]= 1, e[0]= 1, e[1]=2, e[2]=7, e[3]=37, e[4]=266,
c[-5]=-36, c[-4]=-5, c[-3]=-1, c[-2]=0, c[-1]=-1, c[0]= 1, c[1]=0, c[2]=1, c[3]= 5, c[4]= 36,
d[-5]=259, d[-4]=36, d[-3]= 7, d[-2]=1, d[-1]= 4, d[0]=-3, d[1]=1, d[2]=0, d[3]= 1, d[4]= 7. >>823 12C2 = 12! / (2! x 10!) = 12x11 / 2 = 66
>>825 俺の頭が湧いてるのか?
12x11/2 = 11x11=121
わからない、教えて
抽選ボックスが2つ、どちらかから1つからボールを1つだけ引き当選の有無を確認する。
抽選ボックスAはボールが3コ、ボックスBは7コ。
一等は1本、2等は2本、計3本がどちらかのボックスに偏っているとする。
この時どちらのボックスを引くのが良いか?または同じか?
>>828 > 一等は1本、2等は2本、計3本がどちらかのボックスに偏っているとする。
コレは
X : Aに一等1.二等2.Bは全部ハズレ
Y : Bに一等1,二等2,ハズレ4,Aは全部ハズレ
のいずれかであるという意味?
XとYが同様に確からしいとか、なんか条件ないと答えでないんじゃね?
同様に確からしいなら明らかに Aの方がお得だけど。
>>829 同様に確かと言えるのは3/10が当たりということとどちらかに偏ることは確かだとしか聞いてない
A:1/2 ×3/10=3/20
B:1/2 ×3/7/10=5/7
でBの方がお得になるんだけど感覚として
Aは1/2 ×1/3=1/6で当たり引けるから混乱してる
ランダムに分けるんだけど結果偏っていたという場合の考察
全ての分け方: 10C3通り
うちAに当たりが偏った分け方 : 1通り
うちBに当たりが偏った分け方 : 7C3通り
>>830 >A:1/2 ×3/10=3/20
この10はどこから出てきたw
>>832 10個からボール1つを選ぶけどAは3個しかない
(a) A に偏っている場合
3つのボックスのどれかを開ければ1/3の確率で1等、2/3の確率で2等
1等、2等のいずれかが当たる確率は100%
(b) B に偏っている場合
7つのボックスのどれかを開ければ1/7の確率で1等、2/7の確率で2等
1 等、2等のいずれかが当たる確率は3/7≒43%
Aに偏っているかBに偏っているかが同様に確からしい
(それぞれ1/2の確率)ならA の箱を開ければ1/2の確率で当たりをひける。
じゃなくて「ランダムに分けたんだけどなんか偏っちゃった!」だと
そもそもAに偏ってる(=当たりが入っている)確率自体がとても低いのでAを選ぶのは危険
>>834 そうかー
そのランダムなんだけどAってどれくらいの確率なの?
1/10c3か?そりゃ低いや
大きい箱の方に引っ張られるのかね
ボックスAに一等が入っているなら
ボックスBに二等が二つ
ボックスBに一等が入っているなら
ボックスAに二等が二つ入っている
という意味だよ
ごちゃごちゃする前に出題者です。
たとえ話でその後の回答ないので私の方から回答しに来ました。
一般的な確率でなくLOTOを計算しております。
10個のボールの中で前提が1等が1個だけで抽選をし、1等の箱が決まった時点でその箱の中で2等が決まるため同じ箱に偏るとしました。
なので834さんがお答えの通りかなり低いです。1等が3つのボールの箱に入らなければ2等はありませんから。
箱自体に当たりのある確率で30:70です。
>>824 正解です。素晴らしい。
ちなみに用意の解答
―-
f(n,x) = (-1/x d/dx)^n (exp x/x)
とおけば
x^2 f(n,x) = (2n-1)f(n-1,x) + f(n-2,x)。
とくに p[n] = f(n,1)、q[n] = f(n,-1)とおけば
p[n] = (2n-1)p[n-1] + p[n-2]、q[n] = (2n-1)q[n-1] + q[n-2]。
これとp[1] = 0、p[2] = e、q[1] = -2/e、q[2] = -7/eにより
c[n] = p[n]/e、d[n] = (-7p[n]/e + 2e q[n])2。
一方で (-1/x d/dx)^n (exp x/x)をマクローリン展開して lim[n→∞] f(n,±1)/(2n)!! = ±1。
以上により
lim[n→∞] c[n]/(2n)!! = 1/e、lim[n→∞] d[n]/(2n)!! = (-7/e+e)/2。
―
前わかスレに出てた変形ベッセル関数による表示を利用しています。
(本来のベッセル関数だとx=-1を代入できないのでちょっと一工夫してますが。)
それなら
Aに1等が入っている確率3/10
Aから選んで1等を当てる確率3/10x1/3=1/10、2等になる確率3/10x2/3=2/10
Bに1等が入っている確率7/10
Bから選んで1等を当てる確率7/10x1/7=1/10、2等になる確率7/10x2/7=2/10
となるからA、Bのどちらの箱を開けても損得はない
偏りがある。当たる確率は1/10。
流石LOTOどちらも満たしてるね。
あ、
>>839の分母の (2n)!! の所 (2n-1)!! です。
>>838 >>840 回答ありがとうございます。納得しました
あー確率的に同じで偏りがあるから低くなるのか
・a[1]=2
・a[n+1]=a[n]/(1+a[1]+a[2]+…+a[n])
・b[1]=2
・b[n+1]=b[n]/{a[n]+(b[1]+b[2]+…+b[n])/n}
である数列{a[n]}および{b[n]}について以下の問いに答えよ。
(1)極限 lim[n→∞] a[n] を求めよ。
(2)極限 lim[n→∞] b[n] を求めよ。
(1)
エジプトのシエネという町では、年に一度、夏至の日の正午にだけ深い井戸の底まで太陽の光が差し込む。
シエネの北緯は何度か。
hint: 地球の自転軸は公転軸から 23.4°傾いている。
(2)
エジプト第2の都市アレキサンドリアはシエネのほぼ北にあり、その距離は 925 km である。
天文観測から、緯度の差が約 7.2°と分かった。
地球の半径(m)を概算せよ。
なお、経度の差は小さいので無視してよい。
(実際のアレキサンドリアの緯度 31.22゚N、緯度の差 7.82°)
(距離の単位は スタジア = 185 m が使われていた。)
(3)
司天台(浅草天文台)は伊能忠敬の住居(隠宅)のほぼ北にあり、その距離を測量したところ 2482 m だった。
天文観測から、2ヵ所の緯度の差は 約0.025°であることが分かった。
地球の半径(m)を概算せよ。
なお、経度の差は小さいので無視してよい。
(実際の緯度差は 0.02690°、距離は 3025 m、方位角 9.4゚W)
(距離の単位は 町、間が使われている。)
>>844 伊能忠敬の住居(隠宅)は
〒135-0048 江東区門前仲町1丁目18-3先
緯度 35.67452゚N
経度 139.79422゚E
司天台(浅草天文台)は
〒111-0053 台東区浅草橋3丁目20-12
緯度 35.70142゚N
経度 139.78876゚E
にあった。
・おもしろ地図と測量
http://www5a.biglobe.ne.jp/kaempfer/ac-main.htm → 史跡所在リスト
(4) 地球を「GRS80楕円体」として、この2ヵ所の距離と方位角を計算せよ。
・GRS80楕円体
長半径(赤道半径)a = 6378137(m)
扁平率 f = 1/298.257222101
・測量計算(距離と方位角の計算)- 国土地理院
http://vldb.gsi.go.jp/sokuchi/surveycalc/surveycalc/bl2stf.html → 十進法度単位
そうだったのか…
伊能氏が身を削るようにして日本各地の正確な緯度・経度を決めていったのは
地面が曲がっている影響を補正することで、天文予測の精度を画期的に向上するためだった。
日本地図はオマケだった。
>>795 この問題でQの方が有利になるならば、横長い形をしたマス目のうち2マスに宝を埋めた場合縦に沿って探すより横に沿って探した方が勝ちやすいことが一般の場合にも言えるであろうことが容易に想像出来るわけだけど、その証明は出来るだろうか?
高校数学で解けるであろう問題を2つほど
次の定理を示せ
1. 任意の正の整数は連続しない(則ち,項番号が隣りあわない)フィボナッチ数の和として一意的に表される
2. L_(n+2)=L_(n+1)+L_n, L₁=1, L₂=3
を満たす数列(L_n)は任意の素数pに対してL_p≡1 modpを満たす
序でに1問目は「ゼッケンドルフの定理」,又2問目に出てくる数列は「フィボナッチ数列に付随するリュカ数列」(「ルカス数列」「ルーカス数列とも云う)なる名前が付いているらしい
>>843 S = 1 + Σ(k=1,∞) a[n] = 3.91202535564143
(1)
a[n] ~ 11.12728469988 / S^n → 0 (n→∞)
(2)
b[n+1] ≒ n・b[n]/{b[1]+b[2]+…+b[n]} → 1,
>>795 シミュレーションしてみた。
1万回からPの方が先に見つける頻度を出すのを1万回繰り返したときの確率は
> summary(re)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.3749 0.3906 0.3939 0.3939 0.3972 0.4132
となって0.5より小さいのでQの方が有利という結果になった
Rでのスクリプトはこれ
x=c(1,1,rep(0,10))
is.P1st <- function(){
Q=sample(x)
z=matrix(Q,ncol=4,byrow=T)
P=as.vector(z)
which.max(P) < which.max(Q)
}
re=replicate(1e4,mean(replicate(1e4,is.P1st())))
summary(re)
>>852 シミュレーションにバグがある。
同時に見つける場合を考えてなかったわ
>>853 シミュレーションしたら >822の通リになりました。
> x=c(1,1,rep(0,10))
> PQ <- function(){
+ Q=sample(x)
+ z=matrix(Q,ncol=4,byrow=T)
+ P=as.vector(z)
+ c( even=which.max(P) == which.max(Q),
+ p1st=which.max(P) < which.max(Q),
+ q1st=which.max(P) > which.max(Q))
+
+ }
> k=1e6
> re=replicate(k,PQ())
> mean(re['even',]) ; 13/(26+27+13)
[1] 0.197025
[1] 0.1969697
> mean(re['p1st',]) ; 26/(26+27+13)
[1] 0.393803
[1] 0.3939394
> mean(re['q1st',]) ; 27/(26+27+13)
[1] 0.409172
[1] 0.4090909
>795
縦mマス、横nマスのm*nマスのうちランダムに選ばれたkマスにそれぞれ宝が眠っている。
AEIBFJ…の順で縦に宝を探していく方法をとるP君と、ABCDEFGH…の順で横に宝を探していく方法をとるQ君が、同時に地点Aから探索を開始した。
どっちの方が有利?
という風に一般化してみた。
>822のカウントをRでやってみた。
例えば
縦5マス、横10マス、宝3マスだと
P1st Q1st even
8832 9142 1626
(P1stはPが先に宝を発見する宝の配置の数)
Rのコードはここにおいた
Executeのクリックで実行(数値を変えて実行も可能)
http://tpcg.io/Ejjcs2 ある中学入試の問題だけど
方程式なしで小学生はどうやって解くのだろう?
ある牧場では100頭の羊を放すと15日間で牧草がなくなり、120頭の羊を放すと10日間で牧草が食べつくされました。
この牧場で80頭の羊を10日間放した後、さらに何頭xかの羊を加えたところ、加えてから4日間で牧草は食べつくされました。 後から加えた羊は何頭ですか。
ただし、牧草は1日に一定量a生え、また、どの羊も1日で同じ量uの牧草を食べるものとします。
方程式を立てていいなら
1500u=15a + b
1200u=10a + b
a=60u
b=600u
80*14u + 4xu = 14a + b =14*60u + 600u
x=(14*60+600-14*80)/4
で俺でも答えられる。
>>856 線分図の左がはじめの草の量、
右がそれぞれ14回、9回分増えた草の量
(○の中の数字は1日に草の増える量)
(a) 100頭15日(のべ1500匹)├───┼─────┤⑭増える
(b) 120頭10日(のべ1200匹)├───┼───┤⑨増える
するとのべ300匹で⑤だけの草を食べることができる
草を①だけ食べるには60匹必要
(b)を使うと、のべ1200匹が食べた草の総量は1200÷60で⑳と求まる
よってはじめの草の量は⑪
(c) 80頭10日(のべ800匹)├───┼───┤⑨増える
このうち、10日経った時点で(800/60)=(40/3)食べられるので
残りは⑳-(40/3)=(20/3)
あと4日間で全体は(20/3)+④=(32/3)になるので
これを食べるには、4日間でのべ60×32/3=640頭必要
1日あたり160頭必要ということだから、160-80=80頭増やしたことになる
>>857 前日まで生えた分だけでなくその日にリアルタイムで生えているのも食べるから増えるのは15日と10日分では?
>>858 確かに
⑭は⑮に、⑨は⑩に訂正すると
はじめの草の量は⑩になって、あとは大丈夫そうですね
>>859 (800/60)=(40/3)は80頭が10日で食べた量は40/3(13.33)日で生えた
草の量だが⑳-(40/3)=(20/3)の意味不明。
はじめあった草の量⑩も出てこないし。
>>860 (c)の図(10日目が終わった時点)で
はじめの草の量⑩に、10日間で増える草の量⑩を加えて⑳
80頭の羊はそのうち(40/3)を食べてるので、
10日目が終わった時点で残りの草の量は(20/3)
という意味です
>>861 理解できました。
一匹の羊が1日に食べる量を1unitとして考えた方が易しくないかな。分数も出てこないし。
1日に60unit草が生える、最初の草量は600unit。
(100×15-120×10)/5 = 60 だからこの牧場はストック0でも自然増加分で60頭の羊が賄える。
最初のストックは容量を120-60=60頭超過した時10日で食い尽くす量だから600頭日分。
容量超過が80-60=20頭の時10日で減らしたストックは200頭日分だから残りストックは400頭日分。
それを4日で食べ尽くしたので最後の4日の容量超過は100頭。
増えた羊は80頭。
大量に入荷したアルヨ
ε ⌒ヘ⌒ヽフ
( ( ・ω・)
ε ⌒ヘ⌒ヽフ⌒ヽフ
( ( ・ω・) ω・)
ε ⌒ヘ⌒ヽフ⌒ヘ⌒ヽフ⌒ヽフ
( ( ・ω・) ( ・ω・)ω・)
ε ⌒ヘ⌒ヽフ⌒ヘ⌒ヽフヘ⌒ヽフ⌒ヽフ
( ( ・ω・) ( ・ω・) ・ω・)ω・)
しー し─Jしー し─J し─J ─J
■最初からある草の量をbとおく
15a+b=1500u……①
10a+b=1200u……②
②からb=1200u-10aこれを①に代入して
15a+1200u-10a=1500u
5a=300u
a=60u
b=600u
80頭の羊はx頭の羊を加えられた後も牧草を
食べつづけるので 80x14u
x頭の羊は4日間牧草を食べるので 4xu
14日間で消費される牧草の量は 14a+b
80x14u+4xu=14a+b
4xu=14a+b-80x14u
=14x60u+600u-80x14u
=840u+600u-1120u
=1440u-1120u
=320u
∴x=320u/4u=80
>>865 方程式は問題とともに既出なのだから
レスを重ねるなら別解か誤答でないと芸にならんぞw
数字の1と2だけを使って整数を作り、小さい方から並べます。1,2,11,12,21,22・・・このとき、次の問に答えなさい。
(1)1212121212は小さい方から数えて何番目ですか。
任意の自然数nに対して、2005^n が、互いに素な2つの整数の平方和で表せることを示せ。
>>867 1364番め
digi = function(x){ # 1000 -> 4 , 999 -> 3
n=ceiling(log10(x))
ifelse(10^n==x,n+1,n)
}
n2a <- function(num){ # nmu to array 122 -> c(1,2,2)
N=10
r=num%%N
q=num%/%N
while(q>0){
r=append(q%%N,r)
q=q%/%N
}
return(r)
}
one2n <- function(x){ # 121 -> 13
a=n2a(x)
k=digi(x)
p=2^((k-1):0)
sum(a*p)
}
x=1212121212
> one2n(x)
[1] 1364
>>867 (2)1000番目にくる数は何ですか?
Prelude Data.List> let xs = concat $ iterate (¥x->[1:n| n<-x] ++ [2:n|n<-x]) [[1],[2]]
Prelude Data.List> xs !! 999
[2,2,2,2,1,2,1,1,2]
>>868 2005 = (20^2 + 1)(2^2 + 1) = 41^2 + 18^2 = 39^2 + 22^2,
下の公式により 2005^n は2つの平方の和。
互いに素となるかどうか…
〔公式〕
(aa+bb)(㏄+dd) = (ad-bc)^2 + (ac+bd)^2 = (ad+bc)^2 + (ac-bd)^2,
http://www.quora.com/How-can-I-prove-that-a-2+b-2-c-2+d-2-ad-bc-2-+-ac+bd-2 >>870 library(gtools)
perm=permutations(2,9,v=1:2,rep=T)
onetwo=function(x){
n=length(x)
sum(x*2^((n-1):0))
}
perm[which(apply(perm,1,onetwo)==1000),]
> perm[which(apply(perm,1,onetwo)==1000),]
[1] 2 2 2 2 1 2 1 1 2
と総当たりで出すには出せるが、全くエレガントでない :(
>>868 N(a+bi) = a^2 + b^2 として ((20+i)(2+i))^n = u + vi とおけば
2005^n = (N(20 + i)N(2+i))^n = N(((20+i)(2+i))^n) = u^2 + v^2
ここで (u,v) のZ[i] における素因子 p + qi をとれば p - qi | (u,v) | u + vi でもある。
しかし Z[i] は UFD だから p+qi = (20+i)i^e、(2+i)i^e とおける。
このときいずれにせよ p - qi = (20-i)(-i)^e、(2-i)(-i)^e は u + vi の素因子でないので矛盾。
>>850 (1)
正整数nについての帰納法で。
・n≦3 のとき
1 = F_2、2 = F_3、3 = F_4
* 「和」は1項だけの場合もある。
・n>3 のとき
nを超えない最大のフィボナッチ数を F_m とする。 F_m ≦ n < F_{m+1}
もしも和が F_m を含まないなら、
Σ(k=0,[(m-2)/2]) F_{m-1-2k} = Σ(k=0,[(m-2)/2]) ( F_{m-2k} - F_{m-2k-2} ) = F_m - 1 < F_m ≦ n,
となり矛盾する。 よって、和は F_m を含む。
帰納法の仮定により、n - F_m は連続しないフィボナッチ数の和である。
n - F_m < F_{m+1} - F_m = F_{m-1}
∴ n - F_m に対する和は F_{m-1} を含まないから F_m と連続しない。
∴ nについても命題が成立する。
>>867 その数列において、k桁の整数は2^k個含まれる
1212121212は10桁だが、1桁から9桁のすべての数の項数はΣ[j=1,9]2^j=1022
11********台は2^8=256個
1211******台は2^6=64個
121211****台は2^4=16個
12121211**台は2^2=4個
よって
1212121212は1022+256+64+16+4+2=1364項目
>>870 1022項目が222222222なので、これの22項前を考える
2222*****台が32項あるので、
222211111は第991(=1022-32+1)項となる
222211222が第998項なので、第1000項は222212112
>>867 > 1,2,11,12,21,22・・・
10, 11, 100, 101, 110, 111,...
1→0, 2→1 と置き換え、左端に1を付け加えたものを2進数とみなすと
順序を含め2以上の整数と一対一に対応する。
1212121212 → 10101010101(2) = 1365 であるから、1212121212は1364番目。
>>870 1001 = 1111101001(2) であるから、1000番目にくる数は 222212112。
>>879 お見事です。
2進法に似ているのは気づいたのですが
>左端に1を付け加えたもの
ってどういうとこから思いつくのでしょうか?
>>879 お知恵を拝借して 1億個めと1兆個めを計算してみました。
> digit12(10^8) # 1億め
12222212122221111211111112
> digit12(10^12) # 1兆め
221211122121211212112121112111111111112
Rのコードはここ
http://tpcg.io/D2sseW >>882 dec2n n = concat . (map show) . reverse . sub
where sub 0 = []
sub num = mod num n : sub (div num n)
main = do
let n=2
putStr "Input integer : "
str <- getLine
let num = read str
putStrLn $ dec2n n num
Haskellだと一京一も2進数にしてくれた。
Prelude> main
Input integer : 10000000000000001
100011100001101111001001101111110000010000000000000001
ゆえに一京めは
11122211112212222112112212222221111121111111111111112
f 1 =[1]
f n = reverse $ f' (n-1) 2 0 1
f' 0 _ _ _ = []
f' n k j i | n `mod` k == j = 1: f' (n-j) (k*2) k (k*2)
| otherwise = 2: f' (n-i) (k*2) k (k*2)
f (10^8)
[1,2,2,2,2,2,1,2,1,2,2,2,2,1,1,1,1,2,1,1,1,1,1,1,1,2]
>>883 10の68乗を無量大数というらしい
無量大数+1を2進数表示できるかやってみた。
Prelude> :main
Input integer : 100000000000000000000000000000000000000000000000000000000000000000001
1110110101100011101000100011000111010100110001001111101100100111010011001010011110101010101010000110001111101110010010111101110101001000010101101100010111000100000000000000000000000000000000000000000000000000000000000000000001
さすが不定長整数を扱えるHaskell。
>>880 > >左端に1を付け加えたもの
> ってどういうとこから思いつくのでしょうか?
思いつくのは無意識の過程で分からないから、それまでに考えていたことをいうと
1と2の二つの文字 → 2進数に関連か? → 2進数に対応させよう
・1→0, 2→1 と置き換えるだけでは 0,00,000などが重なる → 区別するには? → (区別のためのマーカーがあればいい)
・問題の数字列は1桁では2つ、2桁では4つ、n桁では2^n個 → 2進数では? → (左端の1を除いてn桁で2^n個)
⇒左端に1を付け加えればいいかも? → あとは検証
()内はそのとき無意識には考えていたかもしれないけど、意識したのは検証時だったこと。
その前に「左端に1を…」を思いついた。でも無意識でも必要なことだったと思う。
>>886 Wikipediaによると10の372183838819776444413065976878496481295乗とのこと
Prelude> dec2n n = concat . (map show) . reverse . sub where sub 0 = [] ; sub num = mod num n : sub (div num n)
Prelude> putStrLn $ dec2n 2 (100*10^372183838819776444413065976878496481295)
只今、計算中。フリーズするだろうな。
>>887 解説ありがとうございました。その才能は羨ましい限りです。
>>888 残念ながら予想どおり
GNU MP: Cannot allocate memory (size=4204265496)
のエラーメッセージがでて終了しました。
これも中学入試の問題
x/6=(510+x)/21で解けるけど
方程式なしだとどうする?
ある列車が510mの鉄橋を渡るのに21秒かかりました。また、線路のすぐそばで見ていたA子さんの前を列車が通るのに6秒かかりました。 この列車の長さを求めなさい。ただし、列車は鉄橋を渡るときも、A子さんの前を通るときも同じ一定の速度で走ったとものとします。
これも中学入試
A君、B君、C君の3人である作業をすると、終わるまで10日かかります。A君、B君の2人で同じ作業をすると、終わるまで15日かかります。このとき次の問に答えなさい。
(1)C君1人で同じ作業をすると、終わるまで何日かかりますか。
(2)B君、C君の2人で同じ作業を5日間して、残りをA君が1人ですると、さらに17日かかりました。同じ作業をB君1人ですると 何日かかりますか。
方程式を使ってよければ
全作業量をu(適当な単位で30単位とすると計算が楽)として
(a+b)+c)=u/10
(a+b)=u/15
からu/c=30日
5(b+c)+17a=u
5(b+u/30)+17(u/15-b)=uから
u/b=40日
と出せる。
学習塾での特殊訓練も方程式もなしで解く小学生は凄いなと思う。
『列車が鉄橋を渡る』とは何か?
鉄橋の始点をa、終点をbとすると
列車の先頭がaを通過してから列車の最後部がbを
通過するまでである
区間[a,b]に列車の長さxを足したものを
通過時間で割ると (510+x)/21……①
xが点Aを通過する時間でxを割ると x/6……②
列車は①と②を同じ速度で走るので
(510+x)/21=x/6
6(510+x)=21x
3060+6x-21x=0
15x=3060
∴x=204
>>893 方程式は問題とともに既出なのだから
レスを重ねるなら別解か誤答でないと芸にならんぞw
>>890 列車が鉄橋を渡り終わるのは、
鉄橋と自分の長さを合わせた距離を走ったとき
自分の長さは6秒で走れるので、鉄橋の長さ510mは21-6=15秒で走ることができる
よって列車の速さは510/15=34(m/s)
ゆえに列車の長さは34×6=204(m)
列車の長さxは6秒、鉄橋の長さ+xは21秒で通過する
つまり、鉄橋の長さは15秒で通過する
15/6=2.5なので鉄橋の長さは列車の長さの2.5倍
すなわち、鉄橋の長さ510mの2.5分の1が列車の長さ
∴x=510/2.5=204
これも中学の入試問題
図1のように一辺4cmの正方形にちょうど入る大きさの円Oがある。
図2のように円Oの周上に点Aがあり, OAの中点をMとする。点Aを中心として点Mを通る円をかき, 円Aとする。円Oの周上に点B, Pが, 円Aの周上に点Qがあり, 次の条件をみたしている。
・∠AOB=45°
・BQと円Aは接している
・OPとBQは平行
このとき, 直線AP, BP, 円Oの短い方の弧ABで囲まれた面積として考えられるものをすべて答えなさい。円周率は3.14とする。
図1

図2

>>898 わからんから図だけかいてみたぞ

>>898 >・∠AOB=45°
てか、あれ?こんな条件あったのか?見落としてた……orz
Qの位置とPの位置の組合せで
全部で4パターンあるのかな
>>898 これ大人気なく三角比使えば綺麗に解けるね。
どこの問題ですか?
これ中学入試ってすごいなぁ。
>>795
Ωの部分集合を事象と言う
Ω自身は全事象と言う
最初に探す方向を i
行または列が変わる時を j として
P君とQ君のうちどちらが先に宝を見つけるのかという
事象Aと事象Bを考える.
A={(i,j)| i または j が宝}
B={(i,j)| i または j が宝}
縦方向の探査をn、横方向の探査をn+1とすると
調査する全範囲はn(n+1)
Ω={n(n+1)|(n≧1)}
■縦方向に探査をするP君の確率空間は
Ω={(i,j)|1≦i≦n,1≦j≦n(n+1)}から
#A=n^2(n+1)-{n(n+1)-1}(n-1)
=n^2(n+1)-{n(n^2-1)-(n-1)}
=n^3+n^2-n^3+n+n-1
=n^2+2n-1
#Aは事象Aに含まれる要素の個数
■横方向に探査をするQ君の確率空間は
Ω={(i,j)|1≦i≦n+1,1≦j≦n(n+1)}から
#B=n(n+1)^2-n{n(n+1)-1}
=n(n^2+2n+1)-n(n^2+n-1)
=n^3+2n^2+n-n^3-n^2+n
=n^2+2n
#Bは事象Bに含まれる要素の個数
∴P(A)={(n+1)^2-2}/{n^2(n+1)}
∴P(B)={(n+1)^2-1}/{n(n+1)^2} >>907 読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ。
>>907 読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ。
n=2
> ((n+1)^2-2)/(n^2*(n+1)) + ((n+1)^2-1)/(n*(n+1)^2)
[1] 1.027778
確率が1を超えてるじゃん。
(1)|α|≠r>0を満たす複素数の定数αと実定数rをとる。
|z-α|=rを満たす全てのzについて1/(z')を複素数平面上にとったとき、その図形を求めよ。ただしx'とはxの複素共役である。
(2)xy平面内部に直線x=-1, x=1をとる。
また、点(1/2, 0)または(-1/2, 0)を中心とし、原点を通る円のうちy≧0の部分をそれぞれC_a, C_bと定める。
また単位円のうちy≧0の部分をC_0とする。
任意の自然数kについて、
C_(k-1)とC_aとC_bに同時に接する円のうち中心がx=0かつy>0の領域にあるものをC_kとする。
自然数nについてC_nを求めよ。
>>909 事象Aと事象Bで別々に確率空間が設定されているのに
何で足す必要がある?
>>898 円Oの半径は、
oa=ob=oc=od=2√2
円Oの円周は、
2×3.14×2√2=(12.56)√2
AB=(45/360)×(12.56)√2
=(1.57)√2
OAB=OA×OB×(1/2)
=2√2×(1.57)√2×(1/2)
=2×1.57
=3.14
Pは4点考えられるが、直線ABに対するPの位置は2つと見て、面積は、
3.14×(1/2)=1.57(c㎡)
または、
3.14×(3/2)=4.71(c㎡)
前
>>912修正。
円Oの半径は、
oa=ob=oc=od=2√2
円Oの円周は、
2×3.14×2√2=(12.56)√2
AB=(45/360)×(12.56)√2
=(1.57)√2
OAB=OA×AB×(1/2)
=2√2×(1.57)√2×(1/2)
=2×1.57
=3.14
Pは4点考えられるが、直線ABに対するPの位置は2つと見て、面積は、
3.14×(1/2)=1.57(c㎡)
または
3.14×(3/2)=4.71(c㎡)
>>911 P君とQ君のうちどちらが先に宝を見つけるか、を足した確率がなんで1を超えるんだよ?
>>911 > n=1
> ((n+1)^2-2)/(n^2*(n+1))
[1] 1
前
>>913訂正。
円Oの半径は、2つ掛けあわせて2になる数を○2とすると、
oa=ob=oc=od=2○2
円Oの円周は、
2×3.14×2○2=(12.56)○2
AB=(45/360)×(12.56)○2
=(1.57)○2
OAB=OA×AB×(1/2)
=2√2×(1.57)○2×(1/2)
=2×1.57
=3.14
Pは4点考えられるが、直線ABに対するPの位置は2つと見て、面積は、
3.14×(1/2)=1.57(c㎡)
または
3.14×(3/2)=4.71(c㎡)
>>917 書き方ではなくて概念の話。中学受験なら平方根の概念を用いずに解けるはず。
書き方の問題じゃない。
そもそも間違ってる。
扇型の面積 r^2π/8 の1/2倍とか3/2倍になるはずないやん。
とりあえず
>>898の大人げない解答。
∠AOB = 2θ、OA = r、AM = s、∠ABQ = α とおく。
座標をA(-rsinθ,-rcosθ)、B(rsinθ,-rcosθ)とおく。
Pの座標は(±rcosα,±rsinα)の4通りのいずれか。
このときsinα = s/(2rsinθ)であるから
△PAB
= 1/2 2rsinθ (rcosθ± rsinα)
= 1/2 2rsinθ (rcosθ± rs/(2rsinθ))
= 1/2 (r^2sinθcosθ ± rs)
弦ABと弧ABで囲まれる部分
=1/2 r^2 2θ - 1/2 r^2 sinθcosθ。
∴求める面積
=1/2(r^2 2θ ± rs)
で中学受験に通用するように焼き直せば一応解答は作れる。
>>921 焼き直し例
Oを通りABに平行な直線におろしたPの足をHとおく。
求める面積 - 扇型OAB = △PAB - △OAB = ±1/2 AB・PH。
ここで△OPH∽△BAQによりOP:PH = BA:AQ。
∴1/2 AB・PH = 1/2 OP・AQ。
∴ 求める面積 = 扇型OAB ± 1/2 OP・AQ。
>>921,922
なるほど、見事
ABを底辺と見たときの高さの差に気づくことができれば、
点Hを考えるのは自然ですね
前
>>917もっと近い値がみつかった。(問題
>>898)
ひとまず2個かけあわせて2になる数を√2と書くものとする。
円Oの半径は、
oa=ob=oc=od=2√2(㎝)
円Oの円周は、
2×3.14×2√2=(12.56)√2(㎝)
弧A⌒B=(45/360)×(12.56)√2
=(1.57)√2(㎝)
△OAB=OA×弧A⌒B×(1/2)
=2√2×(1.57)√2×(1/2)
=2×1.57
=3.14(c㎡)
Pは4点考えられるが、直線ABに対するPの位置は2つと見て、扇形ABPの面積は大きいほうが、
3.14+2√2≒3.14+2×1.41421356
=5.96842712(c㎡)
扇形ABPの小さいほうが、
3.14×2-2√2×2√2÷2-(3.14-2√2)
=3.14+2√2-4
≒1.96842712(c㎡)
なるほど簡単な幾何の知識で解ける。
これ中学入試で小学生がやるのか凄いな
子供に教えるとすると
相似の部分を見つけていくという解法かな
>>911 排反事象の確率の和がどうして1を超えるんだよ。
読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ。
>>927 P君とQ君のどちらかが先に
一つでも宝を見つけるとそこでゲーム終了となる
P君の当たりの確率が70%の時に
Q君の当たりの確率が65%あったとしても
何も問題がない
足して135%にはなりません(´・ω・`)
>>928 >>911 > n=1
> ((n+1)^2-2)/(n^2*(n+1))
[1] 1
Pが先
Qが先
PQが同じステップで発見
は 排反事象だから
合計で1にならないのはおかしい。
>>928 その確率求めても面白くないから、
PがQより先に宝を見つける確率や
QがPより先に宝を見つける確率を求めてはどうだろう
>>907
スタート地点のポイントAに宝があると
ゲーム開始とともに同着でゲーム終了になるので除外する
宝がいくつあったとしても、P君とQ君のどちらかが先に
一つでも宝を見つけるとそこでゲーム終了となる
縦方向の探査をn、横方向の探査をn+1として
宝の個数をkと置くと、調査する全範囲は
{n(n+1)-1}-(k-1)=n(n+1)-kと考えられる
Ω={n(n+1)-k)|n≧2,n(n+1)-1>k≧1}
■縦方向に探査をするP君の確率空間は
Ω={(i,j)|1≦i≦n,1≦j≦n(n+1)-k}から
#A=n{n(n+1)-k}-{n(n+1)-k-1}(n-1)
=n(n^2+n-k)-{n(n^2-1)-k(n-1)-(n-1)}
=n^3+n^2-kn-n^3+n+kn-k+n-1
=n^2+2n-k-1
#Aは事象Aに含まれる要素の個数
■横方向に探査をするQ君の確率空間は
Ω={(i,j)|1≦i≦n+1,1≦j≦n(n+1)-k}から
#B=(n+1){n(n+1)-k}-n{n(n+1)-k-1}
={n(n+1)^2-k(n+1)}-{n^2(n+1)-kn-n}
={n^3+2n^2+n-kn-k}-{n^3+n^2-kn-n}
=n^2+2n-k=n(n+2)-k
#Bは事象Bに含まれる要素の個数
∴P(A)={n(n+2)-k-1}/{n^2(n+1)-kn}
∴P(B)={n(n+2)-k}/{n(n+1)^2-k(n+1)} >>934 計算式がないものを答えというのはよくない
今wolframで検算してるけど実に美しい結果が出る
シミュレーションに依存して自分で立式しないのは怠惰の極み
>>930 排反事象になるわけないじゃん
P君の当たりの確率が70%の時に
Q君の当たりの確率が30%に自動的に調整されるなんて
論理的におかしい
P君とQ君は同時に探査を開始するというだけで
それぞれ個別の当たりの確率を保持している
これもしかしてさっきの弦ABの人かな
一貫して全く別のわけのわからない計算してるから無視するよりないな
>>938 当たりの確率ってなあに?
12部屋を順次12回探索するんだから確率1でいずれ当たりを引くんだけど。
あなた以外の人はどちらが早く当てるかを考えてる。
>>940 シミュレーション結果を持って答えだと断定しているけど
計算式があるものとないものを比較して真理値の
判定はできません
P君が1/2でQ君が1/3という結果が出たなら
P君がより早く宝に到達する
>>941 一直線に並んだ12の部屋のどれか1つに宝物があります
あなたは部屋1、2、3、...、11、12の順に探します
私は部屋2、3、4、...、12、1の順に探します
スタートは同時で、部屋から部屋への移動、
部屋の探査に必要な時間は全て同じです。
私は11/12という高確率であなたより先に宝物を見つけます
何故ならあなたが勝つのは宝箱が部屋1にあるときだけで、
これは1/12の確率だからです。
P、Q独立に「確率」を計算しているあなたにはこの理屈が理解できませんし、
この11/12という確率が導けないでしょう。
>>941 >822で随分前に 決着がついている。
列挙して数え上げるには計算式は不要。
読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ。
>>941 >P君が1/2でQ君が1/3という結果が出たなら
>P君がより早く宝に到達する
1の目が3面のサイコロと1の目が2面のサイコロをふったら先に1の目がでるのが前者とは限らんよ。
読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ。
>>941 列挙作業をコンピュータにさせているだけだから言語が違っても(バグがなければ)結果は一致する。
例
http://2chb.net/r/math/1540218853/141-142 乱数発生させての頻度から確率を推測しているわけではない。これが近似すれば列挙作業の検算にはなる。
読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ。
elog[e]πとπlog[π]eの大小関係を示せ。
eを自然対数の底, πは円周率で, それぞれに
2.7<e<2.8, 3.1<π<3.2を与える。
綺麗な解法があります。
(log x)^2/x は 1≦x≦e^2 で単調増加。
六面体のサイコロでP君のサイコロは3面が1、Q君のサイコロは2面が1とする。
サイコロを降ってどちらか一方が1であればそちらが勝者。
どちらも1であるときは引き分け
どちらも1でないならば少なくともどちらかが1がでるまでサイコロをふる。
P君、Q君の勝つ確率を求めよ。
>>950 一回ごとに
P勝ち:3×(6-2) = 12通り、
Q勝ち:(6-3)×2 = 6通り、
引き分け:3×2 = 6通り。
∴ P(P勝ち) = 12/(12+6+6)、P(P勝ち) = 6/(12+6+6)、P(P勝ち) = 6/(12+6+6)。
>>951 こんなことしなくても解けるんだね。
俺はこんな面倒なことして解いた。
方程式なしで解けるロジックを思いつくのはすごいなぁ
p=1/2
q=1/3
q: win
(1-p)*q + (1-p)^2*(1-q)*q+(1-p)^3*(1-q)^2*q+(1-p)^4*(1-q)^3*q+....
=(1-p)*q *( 1 + (1-p)*(1-q) + ((1-p)*(1-q))^2 + ((1-p)*(1-q))^3+...
let r=(1-p)*(1-q)=1/2 * 2/3 =1/3
=(1-p)*q *(1 + r + r^2 + r^3 + ...) = (1-1/2)*1/3 * 3/2 = 1/4 = 0.25
p:win
(1-1/3) * 1/2 * 3/2 = 0.5
draw 1-1/4-1/2= 0.25
引き分けなしの場合:
六面体のサイコロでP君のサイコロは3面が1、Q君のサイコロは2面が1とする。
サイコロを降ってどちらか一方が1であればそちらが勝者。
どちらも1であるときはもしくはどちらも1でないならば どちらか一方だけが1が出て勝者が決まるまで繰り返す。
P君、Q君の勝つ確率を求めよ。
即興でつくった。
船内の加速度で1Gの加速度で船内の時間で1年加速し、船内の時間で1年減速したとき、進んだ距離は?船外の時間で所要時間は?
答え持ち合わせず。
>>954 Σ[1,∞](1/4)^i = 1/4 *(1-1/4)= 1/3
Pr[P:win]=1/2+1/3*1/2=2/3
Pr[Q:win]1/4+1/3*1/4=1/3
で出せるけど、等比数列使わないとどうやるんだろ?
>>948
1<x<4 のとき
log(ex) = 1 + log(x)
= 1 - 2log(1/√x)
> 1 - 2(1/√x -1) (log(y) < y-1)
= 3 - 2/√x
= √x + (2-√x)(√x -1)/√x
> √x, (1<√x<2)
∴ {log(ex)}^2 /x > 1,
x = π/e とおく。 >>941 別スレでは等確率とデタラメ書いてたよなぁ。
http://2chb.net/r/math/1540218853/87 読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ。
>>956
P君が勝つ確率をp,Q君が勝つ確率をq とする。 p+q = 1,
p = (1回で勝つ確率) + (2回目以後に勝つ確率)
= (1回で勝つ確率) + (引分けの確率)・p
= 1/3 + (1/2)p,
q = (1回で勝つ確率) + (2回目以後に勝つ確率)
= (1回で勝つ確率) + (引分けの確率)・q
= 1/6 + (1/2)q,
∴ p=2/3, q=1/3. >>959 ありがとうございました。
すると>956は中学入試の問題にできるんだなぁ。
一回振ってpが1を出す確率が1/2なのにその一回でpが勝つ確率も1/2っておかしいだろ
>>951 >引き分け:3×2 = 6通り。
ここが間違い
双方が1を出す引き分けだけではなく、
どちらも1ではない引き分けも数えなくてはいけない
>>961 最初の問題での設定は
どちらも1でないならば少なくともどちらかが1がでるまでサイコロをふる
という設定。
P勝利をP、Q勝利をQ、引き分けをEとして
、
|P |Q |E |←1回目で決着のうちP、Q、Eの比率が2:1:1 (2/3)
|P |Q |E | ←2回目で決着のうちP、Q、Eの比率が2:1:1 (2/9)
|P |Q |E | ←3回目で決着のうちP、Q、Eの比率が2:1:1 (2/27)
……
結局全体での比率も2:1:1。
>>963 >>951が1/2と間違えてるから指摘しているだけです
>>944 列挙して数え上げるには計算式は不要ですと?
ある事象AとBが起きるときの要素の個数を
洗い出しているだけだから根本的にアプローチが違うのです
査読能力のなさを露呈するのはやめなさい(´・ω・`)
>>945 別に否定はしませんが
P君が1/2でQ君が5/8という場合では
Q君がより早く宝に到達する可能性が高いことを
示しているだけです
■早まった一般化(Hasty generalization)
形式的な誤謬または詭弁の一つ
以下のような論証形式の推論をいう
類推の危険とも
例)
『読んだ人の時間を無駄遣いさせるような明らかな誤答は慎めよ』
■解説
この文章は論理的に妥当ではない
少ない例から『読んだ人の時間を無駄遣いさせる』という
一般的な結論を導こうとしており、これが早まった一般化となる
つまり、自分が時間を無駄遣いさせられるという
一部の個別の事実から全体を判断していて、
それ以外の他スレ住人の中に、時間の無駄と思わない人がいる可能性が
全く考慮に入れられていないため、誤りになる
>>967 効率化に必要なだけで必須じゃなうだろ。
組合せを全部列挙するのは計算式なくてもできる。
表面積1の立体の中で最も良い形の箱を求めよ
ただし、最も良い形の定義は
立体の体積をV,立体を平面に置いたときの接地面の面積をS,定数α>0として、
V+αSが最大となるものである
>>958 デタラメではない
前提条件次第で関数は変化する
宝の個数kを設定するかどうか、ポイントAをどう扱うかによって
複数の種類の関数を作ることができる
>>968 これだね。
当たりの確率ってなあに?
12部屋を順次12回探索するんだから確率1でいずれ当たりを引くんだけど。
あなた以外の人はどちらが早く当てるかを考えてる。
>>972 >複数の種類の関数を作ることができる
そりゃ、どちらも正しくないんだから、いくらでも捏造できるだろ。
>>966 正解はすでに多くの人が書いているように1/3
一回の試行でpが勝つ確率は
pが1を出しかつ q が1以外を出す確率 3/6 * 4/6 =1/3
一回の試行でqが勝つ確率は
qが1を出しかつ pが1以外を出す確率 2/6 * 3/6 =1/6
一回の試行で引き分け試合続行になる確率は
pq ともに1を出す確率 3/6 * 2/6 =1/6 と
pq ともに1以外を出す確率 3/6 * 4/6 =1/3 の和で 1/2
>>975 >
>>950 > 六面体のサイコロでP君のサイコロは3面が1、Q君のサイコロは2面が1とする。
> サイコロを降ってどちらか一方が1であればそちらが勝者。
> どちらも1であるときは引き分け
> どちらも1でないならば少なくともどちらかが1がでるまでサイコロをふる。
> P君、Q君の勝つ確率を求めよ。
一回ごとに
Pの勝つ確率は1/3
Qの勝つ確率は1/6
引き分けの確率は1/6
振り直しの確率は1/3
で結局Pの勝つ確率は?
整数x,yについて 615+x^2=2^y を解け。
>>976
>>950
>六面体のサイコロでP君のサイコロは3面が1、Q君のサイコロは2面が1とする。
>サイコロを降ってどちらか一方が1であればそちらが勝者。
>どちらも1であるときは引き分け
>どちらも1でないならば少なくともどちらかが1がでるまでサイコロをふる。
>P君、Q君の勝つ確率を求めよ。
1回目 P勝 1/3 Q勝ち 1/6 引き分け 1/6 (流れ 1/3)
2回目 P勝 1/9 Q勝ち 1/18 引き分け 1/18 (流れ 1/9)
3回目 P勝 1/27 Q勝ち 1/54 引き分け 1/54 (流れ 1/27)
……
結局 P の勝つ確率は? >>977 yが奇数とするとx^2 - 2z^2 = -615が整数解をもつが 2 は mod 5 で平方剰余でないので矛盾。
よって y は偶数であり z = √(2^y) は整数で x^2 - z^2 = -615を満たす。
(z+x)(z-x) = 615により
(x,z) = (±307、±308)、(±101、±104)、(±59、±64)、(±13、±28)
が必要。
よって解は
(x,y) = (±59、12)。
>>976 >引き分けの確率は1/6
>振り直しの確率は1/3
ああ、ごめんなさい。、誤解してました。
目が1:1のときは振り直さず引き分けになるんですね。
Pが勝つ確率は 1/3 * Σ{n=0..∞} 1/6 = 1/3 * 6/5 = 2/5
Qが勝つ確率は 1/6 * Σ{n=0..∞} 1/6 = 1/6 * 6/5 = 1/5
引き分けの確率は 1/3 * Σ{n=0..∞} 1/6 = 1/3 * 6/5 = 2/5
間違えた
振り直しの確率は1/6じゃなく1/3だから
Pが勝つ確率は 1/3 * Σ{n=0..∞} 1/3 = 1/3 * 3/2 = 1/2
Qが勝つ確率は 1/6 * Σ{n=0..∞} 1/3 = 1/6 * 3/2 = 1/4
引き分けの確率は 1/6 * Σ{n=0..∞} 1/3 = 1/3 * 3/2 = 1/2
が正しい答え
A高校、B高校で試験をしたところ、男子の平均点も女子の平均点もA高校の方が上だったのに
男子女子合わせての平均点はB高校の方が上だったという。
本当にこのようなことがありえるのだろうか?
>>982
シンプソンのパラドックス
ある仮想疾患の治癒率
軽症 重症
国立大学 10/10 10/90
底辺私立 70/90 0/10
自然経過 40/50 5/50
国立大学の方が軽症・重症とも成績がよいが
総数比較では底辺私立の方が成績がよい。
この疾患は自然治癒率が45%とされています。
この疾患の底辺私立での治癒率は70%です。
これに対して国立大学での治癒率はわずか20%です。
という記述も嘘ではないね >>982 A高校、B高校で試験をしたところ、男子の平均点も女子の平均点もA高校の方が上だったのに
男子女子合わせての平均点はB高校の方が上だったという。
A高校 男子10人平均90点 女子90人平均70点 総合平均(10*90+90*70)/100=72
B高校 男子90人平均80点 女子10人平均60点 総合平均(10*90+90*70)/100=78
>>983,984
シンプソンだったか! 名前が思い出せなかったんですよ。
男子女子、重症軽症の比率が(極端に)違うのがポイントのようですね。
>>987 A高校 男子10人平均90点 女子90人平均70点 総合平均(10*90+90*70)/100=72
B高校 男子90人平均80点 女子10人平均60点 総合平均(90*80+10*60)/100=78
の誤記
前
>>987 扇形OAB=3.14c㎡
△OAB=√7≒2.64c㎡
三日月形AB≒3.14-2.64
=0.5c㎡
ABを延長、半直線AB上にPから垂線PCを下ろす。
PC^2=(2√2+√6)^2+(√2)^2-4^2
=14+8√3+2-16
=8√3
扇形OABの高さPC=√(8√3)
扇形PAB=(1/2)AB・PC-三日月形AB
=(1/2)・2・√(8√3)-0.5
=√(8√3)-0.5
=3.2224193
≒3.22c㎡
前
>>990訂正。
扇形OAB=3.14c㎡
△OAB=√7≒2.64c㎡
三日月形AB≒3.14-2.64
=0.5c㎡
ABを延長、半直線AB上にPから垂線PCを下ろす。
PC^2=(2√2+√6)^2+(√2)^2-4^2
=14+8√3+2-16
=8√3
扇形OABの高さPC=√(8√3)
扇形PAB=(1/2)AB・PC+三日月形AB
=(1/2)・2・√(8√3)+0.5
=√(8√3)+0.5
=4.2224193
≒4.22c㎡
>>991 相変わらずの芸風だなぁ。
だいたい中学受験の問題で答えが
>√(8√3)+0.5
になるわけないのに。
AB=2㎝なわけないか。
前
>>991訂正。
扇形OAB=3.14c㎡
△OAB= c㎡
三日月形AB= c㎡
ABを延長、半直線AB上にPから垂線PCを下ろす。
PC^2=(2√2+ )^2+(√2)^2-4^2
=
扇形OABの高さPC=
扇形PAB=(1/2)AB・PC-三日月形AB
=(1/2)・2・√ -
=√ -
= c㎡
仕切りなおしやの。
前
>>994仕切りなおし。
扇形OAB=3.14c㎡
AB^2=(2√2-2)^2+2^2
=8-8√2+4+4
=16-8√2
AB=√(16-8√2)
=2√(4-2√2)
△OAB=(1/2)・2√(4-2√2)・√{(2√2)^2-(4-2√2)}
=√(4-2√2)・√(4+2√2)
=√(16-8)
=2√2
三日月形AB=3.14-2√2
ABを延長、半直線AB上にPから垂線PCを下ろす。
ABの中点をNとすると、
ON=2△OAB/AB
=2・2√2/2√(4-2√2)
=√(4+2√2)
PC=ON+PH
=√(4+2√2)+PH
扇形PABの高さPC=ON+PH
扇形PAB=(1/2)AB・PC-三日月形AB
=√(4-2√2)・{√(4+2√2)+PH}
=√8+PH√(4-2√2)
=√8+√(8-OH^2)(4-2√2)
= c㎡
Pの高さが4つか2つ。
>>973
P(A)をP(B)で割ることによって
P君が先の回数とQ君が先の回数が導ける
P(A)/P(B)=(P君が先の回数)/(Q君が先の回数)
{n(n+2)-k-1}/{n^2(n+1)-kn}
P(A)/P(B)=――――――――――――――――――――
{n(n+2)-k}/{n(n+1)^2-k(n+1)}
=(n+1)(n^2+2n-1-k)/{n^2(n+2)-nk}
∵[n≧2,n(n+1)-1>k≧1]
∵の範囲でnとkの数値をいろいろと変えることにより
様々な勝率が導ける
計算知能にそのまま入力するだけで約分を
自動計算してくれるので試してごろうじろう
■Wolfram入力例
(n+1)(n^2+2n-1-k)/{n^2(n+2)-nk},k=2,n=3 >>907
P(A)をP(B)で割ることによって
P君が先の回数とQ君が先の回数が導けるが
P(A)/P(B)=(P君が先の回数)/(Q君が先の回数)
P(A)/P(B)={(n+1)^2-2}/{n^2(n+1)}/{{(n+1)^2-1}/{n(n+1)^2}}
=(n+1)(n^2+2n-1)/{n^2(n+2)} ∵[n≧1]
宝の個数kを設定しないと精度が低い >>997 この場合、宝の個数は1で固定で全マス探査となる
動かせる数値はnだけ
k動かして正解と同じになるか調べた。
Prelude Data.Ratio> let f n k = (n+1)*(n^2 + 2*n -1-k)%(n^2*(n+2)-n*k)
Prelude Data.Ratio> let g x = let n = (fromInteger x) in (+(0%1)) $ if (odd x) then (1/24*(6*n^3 + 20*n^2 - n - 27)*(n - 1))/(1/24*(6*n^2 + 10*n - 3)*(n + 1)*(n - 1)) else (1/4*n^4 + 7/12*n^3 - 7/8*n^2 - 13/12*n + 1)/(1/24*(6*n^2 - 2*n - 5)*(n + 2)*n)
Prelude Data.Ratio> let h n = head [f n k| k<-[1..], f n k <= g n]
Prelude Data.Ratio> mapM_ print [(g n, h n) | n<-[3..10]]
(26 % 27,8 % 9)
(84 % 83,1 % 1)
(203 % 197,36 % 35)
(413 % 398,28 % 27)
(751 % 722,80 % 77)
(1259 % 1210,27 % 26)
(993 % 955,28 % 27)
(2986 % 2875,88 % 85)
n:3~10で一致するkは一つもみつからん。
時間と労力の無駄。
lud20250126060757caこのスレへの固定リンク: http://5chb.net/r/math/1532793672/
ヒント:5chスレのurlに http://xxxx.5chb.net/xxxx のようにbを入れるだけでここでスレ保存、閲覧できます。
TOPへ TOPへ
全掲示板一覧 この掲示板へ 人気スレ |
>50
>100
>200
>300
>500
>1000枚
新着画像
↓「面白い問題おしえて~な 27問目 YouTube動画>1本 ->画像>46枚 」を見た人も見ています:
・面白い問題おしえて~な 26問目
・面白い問題おしえて~な 30問目
・面白い問題おしえて~な 28問目
・面白い問題おしえて~な 二十二問目
・面白い問題おしえて~な 36問目
・面白い問題おしえて~な 33問目
・面白い問題おしえて~な 35問目
・面白い問題おしえて~な 38問目
・面白い数学の問題おしえて~な 41問目
・面白い数学の問題おしえて~な 42問目
・面白い数学の問題おしえて~な 43問目
・面白い数学の問題おしえて&#65374;な 44問目 (72)
・爆笑問題の漫才が面白すぎる件。これだけの大御所なのに毎年、正統派な面白いネタ書けるって凄いよな
・大学の教養数学の問題おしえろください
・分からない問題はここに書いてね449
・分からない問題はここに書いてね435
・分からない問題はここに書いてね436
・分からない問題はここに書いてね419
・分からない問題はここに書いてね430
・分からない問題はここに書いてね448
・分からない問題はここに書いてね445
・急いでいない問題はここにかいてね3
・分からない問題はここに書いてね438
・分からない問題はここに書いてね440
・分からない問題はここに書いてね455
・分からない問題はここに書いてね422
・分からない問題はここに書いてね451
・分からない問題はここに書いてね420
・分からない問題はここに書いてね418
・分からない問題はここに書いてね450
・分からない問題はここに書いてね446
・分からない問題はここに書いてね433
・分からない問題はここに書いてね454
・分からない問題はここに書いてね442
・【中学数学】分からない問題を教えてください!
・暗記数学で解けない問題は無い
・わからない問題教えてください
・分からない問題はここに書いてね357
・難しい問題を解く力って数学に要らなくね
・分からない問題はここに書いてね425
・分からない問題はここに書いてね460
・分からない問題はここに書いてね465
・分からない問題はここに書いてね463
・分からない問題はここに書いてね459
・分からない問題はここに書いてね415
・分らない問題はここに書いてね403
・分からない問題はここに書いてね 469
・分からない問題はここに書いてね 471
・分からない問題はここに書いてね 470
・分からない問題はここに書いてね429
・分からない問題はここに書いてね 470
・分からない問題はここに書いてね211
・分からない問題を頭が良い人が答えるスレ★
・◆ わからない問題はここに書いてね 163 ◆
・【たかし君】算数みたいな問題文なのに実は超難しい問題を出し合うスレ【釣り】
・『わからない問題はここに書いてね』がひらけないのでここに問題を書かせてくれ!(中学問題)
・この問題の解き方をおしえてほしい
・数学の面白さを教えてくれ
・面白い関数教えてください
・中学2年の数学の問題つくって~
・以前解けなかった問題が容易に解けるようになると成長を実感するよな
・証明問題
・PPAP問題
・この問題教えて
13:38:17 up 73 days, 14:37, 0 users, load average: 12.33, 11.40, 10.91
in 0.098459005355835 sec
@0.098459005355835@0b7 on 063002
|